В современных условиях требуемая комфортность внутреннего микроклимата в помещениях, как правило, поддерживается за счёт того или иного автоматического управления оборудованием обслуживающих данное помещение климатических систем. Максимальная точность при этом обеспечивается, конечно, в случае реализации регулирования по непрерывному закону, в первую очередь с интегральной составляющей, поскольку это даёт нулевую статическую ошибку.
Оценка происходящих при этом тепловых процессов в общем случае является достаточно сложной, так как обычно требует существенного учёта теплообмена на поверхностях ограждающих конструкций и конвективного теплопереноса в исследуемом объёме, а также нестационарной теплопередачи в массиве наружных и внутренних ограждений. Кроме того, необходимо использование уравнений связи между контролируемой температурой в помещении и величиной компенсационного теплового потока от управляемых систем обеспечения микроклимата.
Поэтому решение подобных задач чаще всего производится с помощью составления систем дифференциальных и алгебраических уравнений, которые затем решаются главным образом численными методами, и результирующие зависимости могут получаться весьма сложными [1–7].
В работах [8, 9] автором были найдены расчётные соотношения для основных параметров, характеризующих нестационарный тепловой режим помещения, обслуживаемого автоматизированной системой кондиционирования воздуха, регулируемой по интегральному закону, при условии, что отсутствует фоновый нерегулируемый приток, а теплопоступления Qпост [Вт] меняются скачкообразно от нулевого значения. В первую очередь речь здесь идёт о моменте времени τmax [с], для которого в помещении наблюдается максимальное отклонение температуры воздуха от уставки θmax [К] и о самóм уровне этого отклонения:
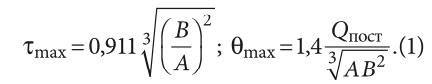
В данном случае числовой коэффициент 0,911 = (3,48/4)2/3, где 3,48 — значение безразмерного времени:

являющегося аргументом при вычислении θmax, а 1,4 = 21/3×1¹∕₉, где 1¹∕₉ — наибольшая величина безразмерной избыточной температуры [8, 9]. Величина A [Вт/(К·с)] относится к характеристикам системы автоматического регулирования. Выражение для A по определению записывается следующим образом:

где Gп — массовый расход приточного воздуха, кг/ч; cв — его удельная теплоёмкость, cв = 1,005 кДж/(кг·К); Крег — эквивалентный коэффициент передачи автоматизированной системы по каналу «tв → производная от tп», с-1.
Параметр B [Вт·с1/2/К] в формулах (1) характеризует теплоинерционные свойства помещения и может быть вычислен так:
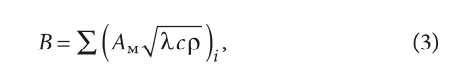
здесь λ — теплопроводность, Вт/(м·К); c — удельная теплоёмкость, Дж/(кг·К); ρ — плотность материала слоя i-го массивного ограждения, обращённого внутрь помещения, в первую очередь наружных и внутренних стен и перегородок, а также перекрытий между этажами; Aм — площадь каждой из данных конструкций, м² [причём «лёгкие» (безынерционные) ограждения, например, заполнения световых проёмов, при этом не учитываются].
Однако выражения (1) содержат величину A, зависящую от Крег, которая, строго говоря, является определяемым, искомым параметром, поэтому в указанном виде они непосредственно пригодны только для поверочных расчётов при заданных характеристиках регулятора. Следовательно, целесообразно было бы так перестроить полученные соотношения, чтобы они содержали только исходные данные, а именно значения Qпост и B, а также допустимую динамическую ошибку регулирования, то есть наибольшую величину θmax. Покажем, как это можно сделать, используя исключительно зависимости (1)-(3).
Во-первых, из первой формулы (1) можно независимо найти параметр A:

где, очевидно, 0,87 = 3,48/4. Теперь подставляем данное выражение в формулу для θmax из (1):
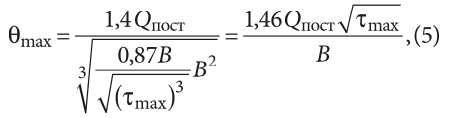
где множитель 1,46 = 1,4/0,871/3, откуда, поскольку обычно задаётся именно величина θmax, находим:
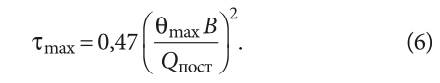
здесь 0,47 = 1/1,462.
Заметим, что соотношение (6) с точностью до числового коэффициента совпадает по форме с полученной автором в [10] зависимостью для времени включения или отключения системы нагрева/охлаждения, регулируемой двухпозиционно («включено/выключено»), что говорит об общности закономерностей происходящих в обоих случаях процессов и дополнительно подтверждает данный результат. Кроме того, нетрудно объяснить также то обстоятельство, что числовой коэффициент в (6) оказывается больше, чем найденный в [10] для двухпозиционного регулирования (¼), поскольку в последнем случае между включениями и выключениями системы фактически имеет место неуправляемый тепловой режим, а в настоящей работе речь идёт о непрерывном регулировании, которое, разумеется, замедляет процесс достижения температурой максимально допустимого отклонения.
Для условий примера из [10], когда Qпост = 500 Вт, B = 24 кВт·c1/2/К, а θmax = 1 К, в соответствии с (6) получаем:
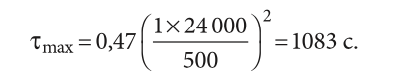
В то же время натурные замеры [10], выполненные в соответствующем помещении с использованием местной системы охлаждения в виде сплит-системы с имитацией скачка теплопоступлений с помощью конвективного электрического тепловентилятора, дают значение τmax = 755 с или примерно на 30% меньше. Однако такое расхождение можно объяснить тем, что в действительности для системы охлаждения применялась комбинация непрерывного и позиционного регулирования, поэтому реальное время достижения допустимого отклонения температуры оказалось промежуточным между этими двумя крайними случаями. В то же время, по крайней мере, по порядку величины выражение (6) даёт верные результаты.
После этого, используя формулу (2), для искомой величины Крег с учётом (4) и (6) имеем:
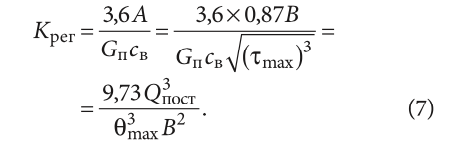
В полученное выражение, так же, как и в (6), входят только исходные данные для расчёта.
Наконец, для безразмерного времени y при вычислении θmax также из (4) и (6) получаем следующую зависимость:
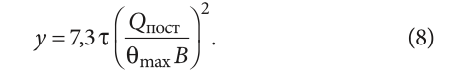
Здесь числовой коэффициент: 7,3 = (21/3×4)2/3,48.
Следовательно, теперь можно рассчитать изменение и текущего отклонения температуры воздуха от уставки θ на основе только заданных величин, независимо от характеристик регулятора, например, с помощью видоизменения аппроксимации, приведённой в [8, 9]:
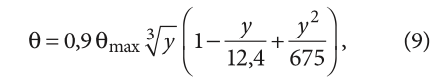
где 0,9 = 1/(1¹∕₉).
Таким образом, мы получили соотношения для основных параметров нестационарного теплового режима помещения, обслуживаемого автоматизированными климатическими системами, управляемыми с применением интегрального закона, позволяющие определять эти параметры с использованием только заранее известных величин и требований к качеству поддержания внутренних метеоусловий. Эти соотношения подтверждаются сравнением разных вариантов аналитических решений, а также сопоставлением с результатами экспериментальных измерений, имеют достаточно простой вид, требуют минимального числа исходных данных и доступны для реализации в инженерной практике.

























