Статья ВАК: Оптимизация функциональных характеристик первичного теплообменника отопительной системы на сверхкритическом СО2

Введение

В сентябре 2023 года Правительство РФ разработало и утвердило комплексную госпрограмму «Энергосбережение и повышение энергетической эффективности» [1]. Главная задача программы — поэтапное, более чем на треть, сокращение использования в России энергоресурсов на единицу продукции. Достижение этой цели, естественно, требует большего внимания к развитию сетей производства электроэнергии за счёт альтернативной генерации, включая использование ВИЭ.

В связи с этим ожидается рост использования мини-ТЭЦ в различных отраслях народного хозяйства и бизнеса, в том числе в сфере туризма. В последнее время в РФ значительно возрос спрос на культурно-познавательный, спортивный, экстремальный, лечебно-оздоровительный, экологический и другие виды туризма, что требует строительства в разных районах страны дополнительных гостиниц и домов отдыха. Следовательно, требуется и подведение дополнительных систем электропитания и отопления. В этом случае мини-ТЭЦ, обладающие свойствами мобильности и адаптации к использованию в самых различных условиях эксплуатации (мини-ТЭЦ может работать на разных видах топлива), могут стать одним из решений возникающей проблемы.

Кроме того, современные мини-ТЭЦ позволяют добиваться весьма высокого КПД использования первичной энергии, в частности, путём утилизации сбросовой тепловой энергии, получаемой от работы двигателя ТЭЦ, посредством теплонасосных установок (ТНУ) [2].

Таким образом, при разработке первичного теплообменника, функционирующего в цикле ТНУ и использующего энергию выхлопных газов (например, газопоршневого ДВС), задача интенсификации процесса теплообмена между потоками горячих газов (продуктов горения природного топлива) и рабочим телом установки весьма актуальна.

Вопросам повышения эффективности использования сбросовой тепловой энергии технологических процессов посвящено, как за рубежом, так и у нас в стране, большое число научных и прикладных исследований. В этой области ведутся поиски рациональных структурных решений теплотехнического оборудования и оптимизации термодинамических циклов [3–5].

Для расчёта теплообменников традиционно используют основное уравнение теплообмена:

Q = kALMTD,

где Q — тепловой поток через поверхность теплопередачи; k — средний общий коэффициент теплопередачи; А — площадь поверхности теплопередачи; LMTD (Log Mean Temperature Difference) — логарифмическая средняя разность температур теплоносителей [6]. Коэффициент теплопередачи k показывает, какое количество теплоты передаётся от горячего теплоносителя к холодному за 1 с через 1 м² поверхности теплопередачи при разности температур между теплоносителями, равной 1 K. Его значение зависит от ряда факторов, в том числе от вклада в общий процесс теплопереноса теплопроводности, теплового излучения, конвекции.

Перенос теплоты в жидкости происходит как бы механически, частицами потока жидкости, и поэтому определяется преимущественно конвекцией. Аналогично конвекцией определяется перенос теплоты через твёрдую стенку, омываемую с двух сторон двумя разными жидкостями, например, в теплообменных аппаратах. Интенсивность теплопередачи в обоих случаях пропорциональна разности температур, а коэффициент пропорциональности, который характеризует теплообмен между поверхностью твёрдого тела и жидкостью, называется коэффициентом теплоотдачи h. Это отношение плотности теплового потока на стенке q к разности температуры стенки Tw и объёмной температуры жидкости Tb:

Коэффициент теплоотдачи показывает, какое количество теплоты передаётся от теплоносителя к 1 м² поверхности стенки (или от 1 м² поверхности стенки к теплоносителю) за 1 с при разности температур между теплоносителем и стенкой, равной 1 K. В отличие от общего для всей конструкции теплообменника коэффициента теплопередачи k коэффициенты теплоотдачи hi характеризуют перенос теплоты в каждом i-м узле, где теплоноситель контактирует со стенкой.

Следует отметить, что в реальных условиях конвекция всегда сопровождается теплопроводностью. Например, в теплообменных аппаратах у поверхности стенки образуется малоподвижный пограничный динамический слой, в котором конвекция ослабляется, так как частицы жидкости или газа, быстро двигаясь в продольном сечении потока, не контактируют непосредственно со стенкой, а действуют на пограничный слой и отдают ему свою теплоту. Дальнейшая передача теплоты стенке происходит в основном путём теплопроводности в направлении нормали к поверхности стенки.

Пусть нормалью к плоскости стенки является ось y и y = 0 соответствует поверхности стенки. При выполнении условия прилипания (то есть при отсутствии проскальзывания) вблизи стенки образуется тонкая плёнка почти неподвижной жидкости. Следовательно, перенос теплоты в этой плёнке осуществляется исключительно за счёт теплопроводности и следует закону Фурье:

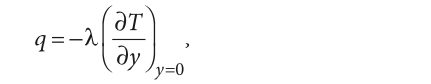
где λ — коэффициент теплопроводности жидкости, и производная температуры T рассчитывается в неподвижном слое жидкости.

Из определения (1) следует формула для вычисления коэффициента теплоотдачи:

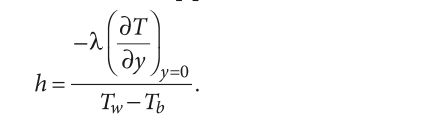
На практике измерить толщину пограничного слоя и рассчитать градиент температуры на стенке можно только для простейших случаев теплопереноса. Широко признанным методом расчёта коэффициента теплоотдачи является использование уравнений подобия и безразмерного числа Нуссельта [7]:

где d — определяющий геометрический размер (например, для потока, движущегося в трубе, d — диаметр трубы). Число Nu характеризует отношение суммарного переноса теплоты конвекцией и теплопроводностью (то есть теплоотдачей) к теплоте, передаваемой теплопроводностью.

Определение (2) позволяет быстро рассчитать коэффициент теплоотдачи для разных условий теплообмена, в том числе при свободной и вынужденной конвекции в задачах внешнего обтекания и при течении в каналах для объектов правильной геометрической формы (горизонтальных и вертикальных плоских поверхностей, цилиндров и сфер). При наличии эмпирической зависимости, основанной на экспериментальных данных, используют корреляцию чисел Нуссельта для расчёта коэффициента теплоотдачи для реальных деталей теплообменников.

Поскольку конвекция, при которой в переносе теплоты участвуют отдельные слои теплоносителя с разными температурами, в отличие от теплопроводности, явление макроскопическое, то конвекцией теплота переносится намного быстрее, чем теплопроводностью. Поэтому режим турбулентности способствует ускорению конвективного переноса теплоты.

Поле температуры и тепловой поток на границе взаимодействия теплоносителя и стенки остаются непрерывными. Однако температура может быстро изменяться в движущейся жидкости: у поверхности стенки температуры теплоносителя и твёрдого тела близки, но чем дальше от границы, тем ближе температура жидкости к температуре на входе в теплообменник или к температуре окружающей среды.

Слой, в котором температура жидкости изменяется от температуры стенки до температуры на входе или окружающей среды, называется «тепловым пограничным слоем». Отношение толщины динамического δr и теплового δt пограничных слоёв выражается числом Прандтля:

здесь cp — теплоёмкость жидкости при постоянном давлении; μ — динамическая вязкость. Число Pr характеризует подобие физических свойств теплоносителей: для того, чтобы оно было равно единице, толщины динамического и теплового пограничных слоёв должны совпадать. Для газов Pr ≈ 1, для жидкостей 10 < Pr < 100.

При вынужденной конвекции поток теплоносителя приводится в движение воздействием внешних сил или устройств (например, вентиляторов или насосов), которые преобладают над силами плавучести. В этом случае режим потока может быть охарактеризован, аналогично изотермическому потоку, числом Рейнольдса:

где ρ — плотность жидкости; u — скорость. Число Re представляет отношение инерционных и вязкостных сил. При малых значениях Re преобладают вязкостные силы, соответственно, поток ламинарный. При более высоких значениях Re силы внутреннего трения в системе невелики, благодаря чему в потоке появляются незначительные возмущения. Если значение числа Рейнольдса будет достаточно большим, поток перейдёт в турбулентный режим.

Оценить толщину динамического пограничного слоя можно с помощью числа Рейнольдса:

При вынужденной теплоотдаче, когда действием силы тяжести можно пренебречь (например, при движении теплоносителей по трубам), числа Нуссельта, Прандтля и Рейнольдса связаны критериальным алгебраическим соотношением Nu = f(Re, Pr), конкретная форма которого зависит от условий течения и находится эмпирическим путём.

Таким образом, из равенства (2) можно найти коэффициенты теплоотдачи для теплообменников различной конструкции [6].

Коэффициент теплоотдачи зависит от многих факторов:

1. Характера движения теплоносителя и его скорости. При турбулентном режиме с увеличением скорости теплоносителя толщина пограничного слоя δr уменьшается и h увеличивается.

2. Физических свойств теплоносителя (динамической вязкости μ, плотности ρ, теплопроводности λ, теплоёмкости c). Коэффициент теплоотдачи h увеличивается с уменьшением μ и увеличением ρ, λ и c. Поскольку физические свойства жидкостей и газов изменяются с температурой T, следовательно, значение h зависит и от T.

3. Размера и формы поверхности теплообмена, а также её обработки (гладкая, шероховатая, загрязнённая).

Коэффициент теплопередачи k теплообменника можно вычислить через коэффициенты теплоотдачи hi отдельных узлов с помощью уравнения аддитивности термических сопротивлений [7]. Для распространённых типов теплообменников известны готовые формулы с учётом конструктивных параметров [6].

В качестве рабочего тела теплонасосной установки для рекуперации вторичной энергии газопоршневого ДВС мини-ТЭЦ рекомендуется использовать диоксид углерода (R744 по классификации хладагентов) с транскритическим переходом (цикл Ренкина) или в сверхкритическом состоянии (цикл Брайтона) [4–5, 8, 10]. Такой выбор связан с уникальными термодинамическими и экологическими свойствами этого хладагента [9, 10].

В ТНУ на сверхкритическом диоксиде углерода (sCO₂) реализуются специфические условия термодинамического цикла, при которых теплообменники в составе таких узлов, как газоохладитель (ГО), рекуператор и первичный теплообменник, функционируют при сверхкритических температуре и давлении. Для оценки эффективности этих узлов ТНУ необходимы проверенные данные о закономерностях теплопередачи между хладагентом и теплоносителем (отопительной водой в ГО или выхлопными газами в первичном теплообменнике), которые можно получить моделированием протекающих в них физических процессов.

К сожалению, обычная методика при построении термодинамического цикла теплотехнического оборудования исходит из предварительно заданной логарифмической средней разности температур на входе и выходе теплообменников и найденных по алгебраическим формулам решений при анализе работоспособности оборудования (и цикла) в целом [6]. Очевидно, что тем самым задача конструктора спроектировать реальный теплообменник под заданный процесс значительно усложняется. Более рациональный процесс конструирования теплообменника должен начинаться с моделирования его функциональных характеристик на основе уравнений в частных производных и решения их методом конечных элементов (МКЭ). В итоге получается геометрия (структура) теплообменника и начальные параметры термодинамического цикла установки, удовлетворяющего поставленной задаче. Построенная математическая модель (цифровой двойник) будет служить для оценки и поддержания надёжности реальной установки в период её эксплуатации, при модернизации и совершенствовании.

В работе [9] авторами проведено моделирование в ПО COMSOL Multiphysics газоохладителя с кожухотрубчатым теплообменником, обеспечивающим температуру отопительной воды около 80°C, в ТН транскритического цикла на sCO₂. Проблема интенсификации работы кожухотрубчатых теплообменников связана главным образом с выравниванием термических сопротивлений на противоположных сторонах теплообменной поверхности. Этого можно достичь: во-первых, систематической очисткой отложений и удалением примесей из теплоносителей; во-вторых, увеличением поверхности теплообмена, например, оребрением её со стороны теплоносителя с меньшим коэффициентом теплоотдачи (в данном случае, sCO₂); в-третьих, увеличением коэффициента теплоотдачи за счёт оптимизации гидродинамики потока sCO₂. Последнее приведёт к выравниванию скоростей и температур в сечении потока теплоносителя, то есть к уменьшению термического сопротивления его пограничного слоя со стороны потока sCO₂, а именно сопротивление пограничного слоя является главным фактором, снижающим интенсивность теплопередачи.

Также теплообмен значительно улучшается при ликвидации застойных зон в межтрубном пространстве со стороны отопительной воды и за счёт искусственного воздействия на разделяющую поверхность элементами, взвихряющими и разрушающими внутренний пограничный слой. Это различного рода вставки (спирали, диафрагмы, диски) и насадки (кольца, шарики), помещаемые в трубу.

Другим видом теплообменников в ТН на sCO₂ являются спиральные теплообменники в виде трубчатого змеевика. Зависимость их характеристик от расположения (горизонтальное или вертикальное), геометрических параметров спирали и различных вставок интенсивно изучается [11–13]. Однако в большинстве работ эти теплообменники рассматриваются в составе ГО или рекуператора, но не первичного теплообменника.

В работе [10] авторами проведено моделирование в ПО COMSOL Multiphysics газоохладителя спирального теплообменника, размещённого в выхлопной трубе ДВС мини-ТЭЦ, и показано, что теплообмен с потоками выхлопных газов позволяет нагревать хладагент R744 до температуры 300°C, необходимой для обеспечения работоспособности ТНУ по циклу Ренкина.

При этом было сделано допущение, что геометрия модели и поток выхлопных газов полностью осесимметричны, и использовался интерфейс 2D axisymmetric с отдельными граничными условиями конвективного теплового потока на внутренних границах каждого витка змеевика. Однако для вычисления коэффициента теплоотдачи на всей поверхности теплообменника и оптимизации его функциональных характеристик необходимо провести дополнительное исследование в 3D-постановке.

Все отмеченные выше факторы повышения интенсивности теплообменников были учтены при моделировании функциональных характеристик разрабатываемого первичного теплообменника.

Исследуемая модель и результаты

В первичном теплообменнике с передачей теплоты от выхлопных газов в межтрубном пространстве к жидкости в трубчатом змеевике (в данном случае сверхкритическому sCO₂) коэффициент теплоотдачи с наружной стороны труб оказывается примерно на порядок меньше, чем с внутренней стороны [7]. Для интенсификации теплоотдачи со стороны менее эффективного теплоносителя в конструкцию теплообменника добавлена вставка, имеющая форму винта Архимеда с образующей поверхностью — частью прямого геликоида, ограниченной двумя соосными цилиндрами диаметрами d1 и d2, соответственно.

Внутренняя и внешняя стенки кожуха глушителя образованы соосными цилиндрами тех же диаметров, так что его центральная часть представляет собой полую трубу. Винт-вставка помещается вертикально в глушитель таким образом, что его боковые грани плотно прилегают к внутренней и внешней стенкам кожуха.

К нижнему и верхнему торцам глушителя присоединены патрубки для подачи и отвода газов из выхлопной трубы ДВС мини-ТЭЦ. Таким образом, потоки выхлопных газов движутся по направлению «снизу-вверх» вдоль направляющей винтовой поверхности, что создаёт их завихрение и усиливает давление на стенки теплообменника. Первичный теплообменник состоит из двух одинаковых спиральных змеевиков, идущих вдоль верхней и нижней поверхностей винта-вставки с теми же шагом l и числом витков N. Тепловой контакт спиралей теплообменника с винтом обеспечен спайкой в зоне их касания. Движение sCO₂ внутри трубок, закрученных по спирали, также сопровождается завихрением и увеличением давления потоков sCO₂ на внутренние стенки [11].

Проведено моделирование и исследование функциональных характеристик данного первичного теплообменника в ПО COMSOL Multiphysics. Результаты моделирования представлены на рис. 1. Геометрия теплообменника в виде парного трубчатого змеевика с винтом-вставкой, размещённого в кожухе глушителя ДВС показана на рис. 1а сечением плоскостью y0z.

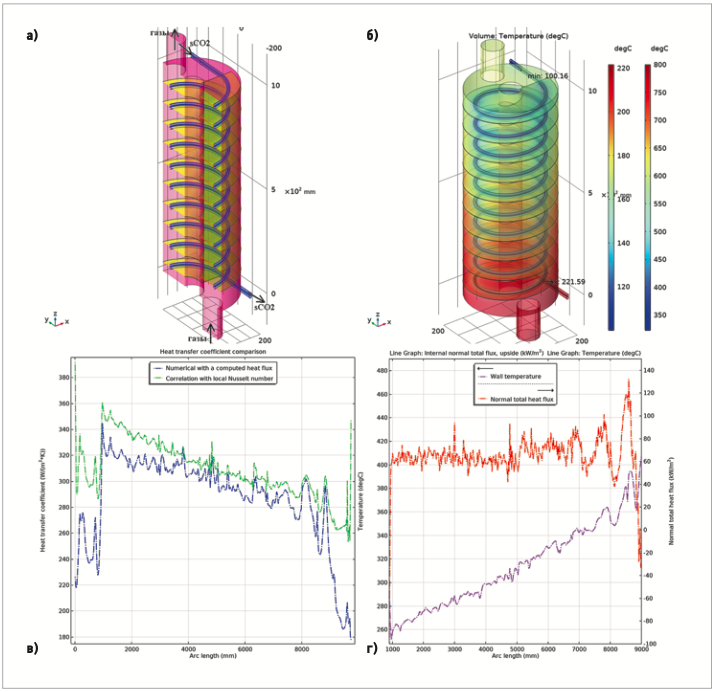
Рис. 1. Геометрия и функциональные характеристики трубчатого змеевикового теплообменника [а — кожух и змеевик с винтом-вставкой, входными и выходными отверстиями (сечение в плоскости y0z); б — стационарное распределение температур хладагента в теплообменнике и выхлопных газов в кожухе; в — сравнение распределений по длине верхней трубки змеевика коэффициента теплоотдачи, вычисленного двумя способами; г — то же для температуры стенки змеевика и плотности теплового потока на ней]

Параметрическая форма задания поверхности винта:

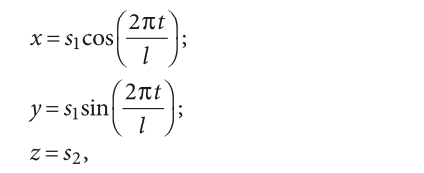
где d1/2 ≤ s1 ≤ d2/2, 0 ≤ s2 ≤ Nl — безразмерные параметры. В данной модели d1 = 0,1, d2 = 0,4, l = 0,096, N = 10, что даёт десять витков винтовой поверхности с шагом 0,096 м и общей высотой 0,96 м.

Трубчатая спиральная поверхность змеевика имеет те же шаг и количество витков, диаметр спирали D = 0,3 м, диаметр трубки d = 12,5 мм, толщина 1,25 мм. На входе и выходе из кожуха глушителя спиральный змеевик продолжается отрезками прямых трубок длиной 0,2 м. Внутренний диаметр кожуха глушителя d1 = 0,1 м, внешний — d2 = 0,4 м. Высота глушителя H = 1 м, винт-вставка толщиной 2,5 мм отстоит от его торцов на 18,75 мм. Торцевые цилиндрические патрубки имеют диаметр 0,1 м и высоту 0,15 м.

Материал кожуха — конструкционная сталь, винта-вставки — алюминий, трубок змеевика — медь. В библиотеке материалов COMSOL отсутствуют данные о свойствах CO₂ в сверхкритическом состоянии. Поэтому теплофизические свойства sCO₂ такие, как вязкость, плотность, теплопроводность, теплоёмкость, были сгенерированы на основе базы данных Национального института стандартов и технологий (NIST) [14] и импортированы в COMSOL как табличные функции температуры и давления.

Параметры входного потока sCO₂ соответствуют модели теплонасосных установок с циклом Ренкина из работы [10]: T1 = 100,2°C, P1 = 31 МПа, m· = 3600 кг/ч. Параметры потока выхлопных газов определяются по характеристикам газопоршневого двигателя MAN E3262 LE232, широко используемого в современных мини-ТЭЦ [15]. Число цилиндров n = 12, рабочий объём цилиндра V = 25,78 л, частота вращения двигателя ν = 1500 об/мин. Тогда объёмный расход потока газов составит V· = nVν/2 = 0,32228 м³/c. Давление после выпускного коллектора равно 1 бар, температура газов на входе в глушитель составляет 800°C.

Физическая модель конвективного теплообмена между потоками выхлопных газов и sCO₂ через стенки трубок змеевика и винта-вставки основывается на интерфейсах Turbulent Flow, k-ε и Heat Transfer in Fluids. Из-за большой разницы давлений потоки в смежных доменах задаются независимо друг от друга, каждый в рамках своего интерфейса турбулентного потока с разными условиями сжимаемости. Для CO₂ выбрано условие «сжимаемый поток», так как его свойства существенно изменяются в зависимости от давления и температуры. Для выхлопных газов на первом этапе решения принято условие несжимаемого потока с приближением Буссинеска, при котором теплофизические свойства зависят от референсных значений температуры и давления, указанных в интерфейсе, что упрощает расчёт. Стационарное уравнение теплопередачи, общее для смежных доменов, содержит в левой части слагаемые, выражающие перенос тепла конвекцией и теплопроводностью, а в правой части — слагаемые, учитывающие как источник тепла работу давления Qp и вязкостных сил Qvd:

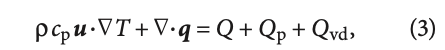
ρcpuNABLA·T + NABLA·q = Q + Qp + Qvd, (3)

здесь q = -kT, Qp = αpTu·NABLAp,

где коэффициент теплового расширения жидкости:

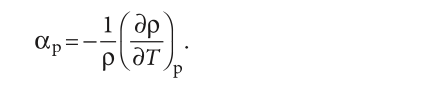
На первом этапе решения мы не учитываем естественную конвекцию, вызванную силой плавучести, которая возникает из-за температурных градиентов. Поэтому действием силы тяжести можно пренебречь. Теплообменник может работать как в прямоточном, так и в противоточном режимах. Далее рассматривается направление потока sCO₂ сверху вниз, то есть противоположно направлению выхлопных газов. Поток sCO₂ делится поровну между верхним и нижним змеевиком.

На рис. 1б приведено распределение температур установившихся потоков выхлопных газов и хладагента в области теплопередачи, соответствующее стационарному решению. Видно, что температура sCO₂ увеличивается по мере прохождения потока хладагента по змеевику: от 100,16°C на входе в верхний (первый) виток до максимума 221,59°C на нижнем (десятом) витке. При этом температуры на выходе теплообменника вне кожуха равны 209,37 и 210,3°C для верхней и нижней трубки, соответственно. Таким образом, нагрев рабочего тела в теплообменнике не достигает необходимой для обеспечения рабочего цикла ТНУ температуры 300°C.

По результатам моделирования в COMSOL можно рассчитать плотность теплового потока q на стенке змеевика, температуру стенки Tw и объёмную температуру хладагента Tb. В то же время для змеевика теплообменника число Нуссельта при вынужденной конвекции можно вычислить по формуле [11]:

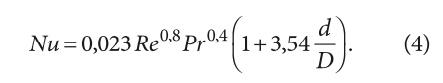
Это даёт возможность сравнить значения коэффициента теплоотдачи, найденные двумя способами. На рис. 1в даны распределения коэффициента теплоотдачи h, вычисленного по определению (1) через плотность теплового потока (синяя линия) и по формуле (2) с помощью числа Нуссельта:

(зелёная линия) по длине верхней трубки змеевика в направлении потока sCO₂, то есть по направлению «сверху-вниз». Хорошо заметна корреляция этих величин на всех участках змеевика: резкие скачки с большой амплитудой на переходе от входного прямого отрезка трубки к спирали, нерегулярные колебания на витках спирали змеевика с убыванием среднего значения от максимума 360–345 Вт/( м²·K) в начале до минимума 264–238 Вт/( м²·K) в конце и резкие скачки на переходе к прямому отрезку на выходе. Для характеристики теплоотдачи поверхности змеевика существенным является только значение h на участке от 1,0 до 9,0 м, где параметры потока sCO₂ становятся устойчивыми. На этом отрезке два способа вычисления h дают близкие значения, что подтверждает точность моделирования.

Поскольку массовый расход и давление хладагента на входе заданы постоянными, а изменения теплофизических характеристик sCO₂ в потоке достаточно плавные, колебания величины h вызваны высокой турбулентностью выхлопных газов с нерегулярными скачками величины теплового потока. На рис. 1 г. показаны распределения температуры стенки змеевика Tw (розовая линия) и плотности теплового потока q на ней (красная линия) в направлении движения sCO₂ («сверху-вниз»). Видно, что величина q колеблется с высокой частотой около медленно возрастающей кривой средних значений от 60 до 80 кВт/м², а температура стенки аналогичным образом возрастает от 250 до 400°C.

Дальнейшее моделирование связано с учётом действия сил гравитации и плавучести. При естественной конвекции движение жидкости обусловлено самим процессом теплообмена из-за разности температур в потоке.

Число Грасгофа Gr показывает отношение сил вязкости к произведению силы плавучести, определяемой разностью плотностей в различных точках неизотермического потока, и силы инерции [7]. Для потока хладагента в трубке теплообменника [12]:

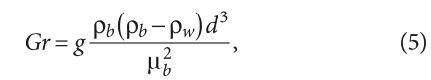
где нижние индексы b и w при обозначениях физических свойств указывают, что они рассчитываются по объёмной температуре Tb и по температуре стенки Tw, соответственно. В зависимости от относительной величины силы плавучести вклад естественной конвекции в теплообмен является неоднозначным и может приводить к противоположным результатам. Его можно связать с «числом плавучести» Bo, различные выражения для которого неоднократно предлагались разными авторами. В данной работе сравниваются традиционная формула [11]:

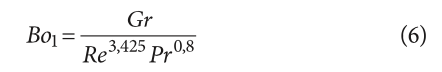
и уточнённая [13]:

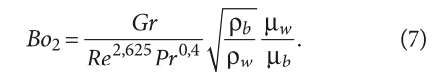
Согласно критерию 1 [11], если Bo1 < 4×10–8, то эффект плавучести невелик, а естественная конвекция недостаточно сильна, чтобы положительно влиять на теплообмен. Таким образом, вынужденная конвективная теплопередача является доминирующей внутри трубки змеевика. В этом случае уменьшение плотности sCO₂ из-за нагрева возле внутренней стенки создаёт неравномерное «тепловое ускорение» в жидкости и приводит к нарушению турбулентности в пристеночном слое и ухудшению теплопередачи. С увеличением Bo1 сила плавучести возрастает, и естественная конвекция начинает оказывать положительное влияние на теплообмен. Но при 4×10–8 < Bo1 < 8×10–7 рост теплопередачи, вызванный естественной конвекцией, не может полностью компенсировать ухудшение теплопередачи из-за нарушения турбулентности. Если Bo1 > 8×10–7, естественная конвекция полностью развита, и нарушение турбулентности вблизи стенки подавляется, что приводит к улучшению теплопередачи. В то же время уточнённый критерий 2 [13] устанавливает для Bo2 пороговое значение 1,3×10–5, ниже которого действием силы плавучести можно пренебречь.

На рис. 2 показано влияние естественной конвекции на функциональные характеристики предложенного теплообменника. На рис. 2а даны распределения числа плавучести Bo1, вычисленного по определению (6) (зелёная линия), и Bo2 по определению (7) (синяя линия) по длине верхней трубки змеевика в направлении потока sCO₂. Видно, что на отрезке от 1,0 до 9,0 м, где параметры потока sCO₂ становятся устойчивыми, Bo1 < 4×10–8, но Bo2 > 10–4. Следовательно, в данном случае влияние силы плавучести на теплообмен отрицательное, а естественная конвекция не создаёт вторичной турбулентности вблизи стенок.

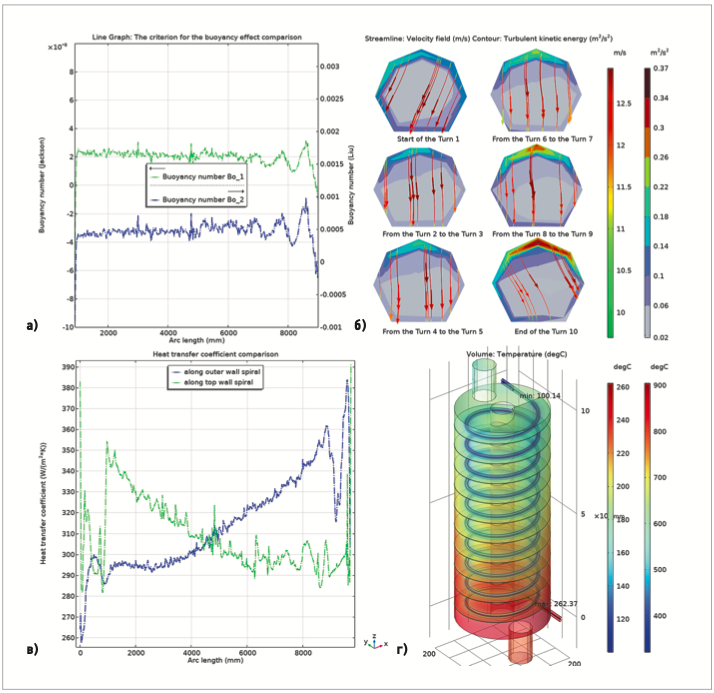
Рис. 2. Влияние естественной конвекции на функциональные характеристики теплообменника [а — сравнение распределений двух вариантов числа плавучести по длине верхней трубки змеевика; б — проекции векторного поля скорости sCO₂ на сечения змеевика в плоскости y0z справа от центральной оси и распределение кинетической энергии турбулентности там же; в — сравнение распределений коэффициента теплоотдачи вдоль верхней и внешней боковой стенки змеевика; г — стационарное распределение температур хладагента в теплообменнике и выхлопных газов в кожухе]

Это объясняется тем, что температура и давление sCO₂ в первичном теплообменнике намного выше критических и свойства сверхкритической жидкости однородны по всему сечению потока, включая пристеночные зоны.

На рис. 2б проекции векторного поля скорости хладагента вдоль оси y показаны для некоторых из сечений змеевика плоскостью x0z справа от центральной оси: в начале первого витка, на стыке второго и третьего, четвёртого и пятого, шестого и седьмого, восьмого и девятого витков, и в конце десятого витка. Легенда графика соответствует полной средней скорости, хотя проекция y-компоненты скорости равна нулю. Также дано распределение кинетической энергии турбулентности в указанных сечениях. Видно, что на входе в первый виток и на выходе из последнего направление потока sCO₂ следует за изменением кривизны трубки змеевика, а в промежуточных сечениях линии скорости отклоняются под действием центробежной силы. В этих сечениях наибольшая средняя скорость (до 12,9 м/с) достигается в середине трубки, а на её внешней стороне скорость течения выше, чем на внутренней. Таким образом, на x-компоненту скорости течения влияет преимущественно центробежная сила, но не сила плавучести.

Распределение кинетической энергии турбулентности показывает её рост от середины сечения (0,01 м²/c2) к границам с увеличением наибольших значений от 0,14 м²/c2 в начале первого витка до 0,37 м²/c2 в конце последнего. При этом зона наибольшей турбулентности сосредоточена у верхней границы сечения, то есть вверху трубки змеевика. При увеличении объёмной температуры sCO₂ на каждом витке область максимальной z-компоненты скорости движется к верхней стенке трубки из-за плавучести, которая толкает нагретую жидкость вверх. Высокая турбулентность в пристеночном слое усиливает теплопередачу, но и температура верхней стенки выше, чем в других областях, что может уменьшить коэффициент теплоотдачи. Таким образом, сила плавучести оказывает комбинированное влияние на конвекцию вблизи верхней стенки трубки, и оценить его можно, сравнив коэффициенты теплоотдачи на верхней и боковой стенках змеевика.

На рис. 2в приведены распределения коэффициента теплоотдачи h, вычисленного по определению (1) вдоль верхней стенки (зелёная линия) и вдоль внешней боковой стенки (синяя линия), по длине верхней трубки змеевика в направлении потока sCO₂, то есть «сверху-вниз». Видно, что при близости средних значений с минимумом около 290 Вт/( м²·K) и максимумом около 360 Вт/( м²·K) графики выражают противоположные изменения. Убывание коэффициента h вдоль верхней стенки объясняется ростом температуры Tw из-за контакта с более нагретой жидкостью, вызванного силой плавучести. Возрастание коэффициента h вдоль внешней боковой стенки объясняется действием центробежной силы на пристеночный слой. Таким образом, действие сил гравитации и плавучести оказывает существенное влияние на характеристики модели и должно быть учтено в решении.

На втором этапе решения в качестве начальных значений для уравнения (3) использованы данные предыдущего исследования. Для выхлопных газов принято условие слабо сжимаемого потока, позволяющее учесть естественную конвекцию. На рис. 2 г. приведено распределение температур установившихся потоков выхлопных газов и хладагента в области теплопередачи, соответствующее стационарному решению. Видно, что температура sCO₂ увеличивается по мере прохождения потока хладагента по змеевику: от 100,14°C на входе в первый виток до максимума 262,37°C на нижнем (десятом) витке. При этом температуры на выходе теплообменника вне кожуха равны 245,78 и 248,12°C для верхней и нижней трубки, соответственно. Таким образом, нагрев рабочего тела всё ещё недостаточен для обеспечения рабочего цикла ТНУ, и необходима оптимизация конструкции теплообменника.

Предложенная конструкция теплообменника позволяет варьировать такие параметры трубчатого змеевика, как диаметр спирали, диаметр и толщину трубки, не изменяя шаг и число витков. При этом не нарушается связь с винтом-вставкой, составляющим каркас теплообменника. Вместе с тем возможно и увеличение общей длины змеевика за счёт добавления на поверхности винта-вставки дополнительных витков спирали. Например, на верхней поверхности можно разместить две соосные спирали разных диаметров, соединив их в общий контур петлёй в верхней части кожуха глушителя. Аналогично на нижней поверхности размещается вторая пара спиралей, образующих второй контур, так что общая длина змеевика увеличивается почти вдвое по сравнению с исходным вариантом.

Геометрия модели оптимизированного теплообменника, в отличие от исходного, включает две пары трубчатых спиральных поверхностей с диаметрами D1 = 0,25 м и D2 = 0,35 м. Остальные параметры совпадают с исходными. Нижние витки сдвоенного спирального змеевика продолжаются отрезками прямых трубок длиной 0,2 м, так что вход и выход из кожуха глушителя находятся на одном уровне. Теплообменник сочетает прямоточный и противоточный режим движения теплоносителей. Далее рассматривается вариант с движением потока sCO₂ от входа в кожух по направлению «снизу-вверх» по внутренней спирали меньшего диаметра, то есть в направлении выхлопных газов, и возвратным движением «сверху-вниз» по внешней спирали, то есть противоположно направлению выхлопных газов. Поток sCO₂ делится поровну между змеевиками на верхней и на нижней поверхностях винта-вставки.

Уравнение (3) решается с прежними начальными условиями с учётом естественной конвекции, как для потока sCO₂, так и для выхлопных газов.

На рис. 3 показан результат оптимизации первичного теплообменника. На рис. 3а приведено стационарное распределение температур выхлопных газов и хладагента в области теплопередачи. Видно, что температура sCO₂ растёт от 100,1°C на входе в первый (нижний) виток внутренней спирали до максимума 325,63°C на выходе из десятого (нижнего) витка внешней спирали. При этом температуры на выходе теплообменника из кожуха равны 305,41 и 310,0°C для верхней и нижней части, соответственно. Таким образом, рабочее тело ТНУ нагревается до необходимой температуры.

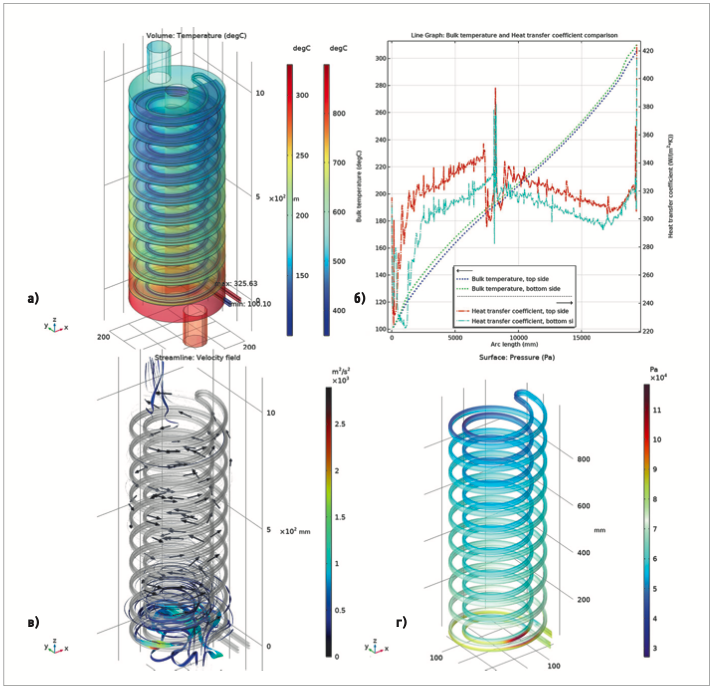
Рис. 3. Функциональные характеристики оптимизированного теплообменника [а — стационарное распределение температур хладагента в теплообменнике и выхлопных газов в кожухе; б — сравнение распределений объёмной температуры и коэффициента теплоотдачи вдоль верхней и нижней спирали змеевика; в — линии потока и поле скорости выхлопных газов пропорционально кинетической энергии турбулентности; г — давление выхлопных газов на стенки змеевика]

На рис. 3б сравниваются распределения объёмной температуры sCO₂ в верхней (синяя линия) и нижней (зелёная линяя) спиралях змеевика и коэффициента теплоотдачи вдоль верхней (красная линия) и нижней (голубая линяя) спиралей. Видно, что температура изменяется синхронно в обеих частях теплообменника с небольшим превышением в нижней части, что обеспечивает равномерный нагрев хладагента и нужную температуру суммарного потока. Напротив, коэффициент теплоотдачи вдоль верхней спирали выше, что объясняется большей плотностью теплового потока на верхней части теплообменника. Скачок в середине графика соответствует переходу с внутренней спирали на внешнюю и не должен учитываться при вычислении среднего значения коэффициента.

На рис. 3в показаны линии потока и поле скорости выхлопных газов вдоль поверхности змеевика. Ширина линий пропорциональна кинетической энергии турбулентности, шкала которой составляет легенду графика. Видно, что турбулентность потока резко возрастает на входе в каналы, образованные винтом-вставкой, с наибольшим значением энергии 2,9×103 м²/с2 на первом витке змеевика. Вторичный рост турбулентности отмечается на выходе из винтовых каналов. Этим объясняются резкие скачки величин плотности теплового потока и коэффициента теплоотдачи в начале и в конце змеевика (рис. 1в, 1 г., 2в и 3б).

На рис. 3 г. показано давление выхлопных газов на стенки змеевика. Видно, что область наибольшего давления (до 1,2×105 Па) также приходится на его нижние витки, вызывая скачки характеристик теплообменника. Таким образом, их нужно определять участках от 1,0 до 7,5 м и от 8,5 до 18 м, где параметры потоков становятся устойчивыми.

Заключение

1. В связи с ростом интереса и развитием различных видов внутреннего туризма необходимо строительство новых гостиниц и домов отдыха. Следовательно, потребуется подведение дополнительных систем электропитания и отопления. Решение возможно за счёт мини-ТЭЦ, которые позволяют достичь высокого КПД использования первичной энергии, в частности, путём утилизации сбросовой тепловой энергии, получаемой от работы двигателя ТЭЦ, применяя её в теплонасосных установках.

2. При разработке первичного теплообменника, функционирующего в цикле ТНУ и использующего энергию выхлопных газов, например, газопоршневого ДВС, весьма актуальной является задача интенсификации процесса теплообмена между потоками горячих газов (продуктов горения природного топлива) и sCO₂ как рабочим телом установки.

3. Проведено моделирование и исследование принципиально новой структурной схемы первичного теплообменника в ПО COMSOL Multiphysics на основе уравнений k-ε-модели турбулентности и теплопередачи в жидкостях с использованием обширной научной базы, заложенной в интерфейсах и библиотеках COMSOL Multiphysics.

4. Показано, что рациональная форма первичного теплообменника со вставкой в форме винта Архимеда и трубчатыми змеевиками на его сторонах сообщает потокам выхлопных газов ДВС мини-ТЭЦ движение вдоль направляющей винтовой поверхности, что создаёт их завихрение и усиливает давление на стенки теплообменника. Аналогичные эффекты обеспечиваются и для потоков sCO₂ в трубчатом змеевике, что позволяет решить ключевые вопросы эффективности функционирования подобных теплообменников.

5. Использование при моделировании функциональных характеристик процесса теплопередачи первичного теплообменника критериев подобия Нуссельта, Прандтля, Рейнольдса, Грасгофа (отражающих, соответственно: теплоотдачу через стенку с учётом совместного действия конвекции и теплопроводности; роль пограничных слоёв вблизи стенки в теплопередаче; влияние турбулентного режима потоков в теплообменнике на теплопередачу; роль отношения сил вязкости и плавучести в конвекции потока sCO₂ и, следовательно, в теплообмене через стенку) позволило осуществить оптимизацию процесса теплопередачи в первичном теплообменнике и получить искомые температурные параметры sCO₂ на выходе из теплообменника.