Статья ВАК: Анализ адиабатного процесса расширения рабочего тела в открытой термодинамической системе с помощью тепловой диаграммы в T–S-координатах

Рассмотрим процесс расширения рабочего тела в адиабатической открытой системе с газодинамическими потерями с привлечением, для наглядности, тепловой диаграммы в T-S-координатах (рис. 1 и 2). Адиабатичность процесса расширения рабочего тела в открытой термодинамической системе требует только отсутствия теплообмена с внешней средой и постоянства теплоёмкости, но не требует постоянства энтропии, поэтому адиабатичность совмещается с постоянством энтропии в потоке только в изоэнтропном процессе, называемом ещё «идеально-адиабатическим».

Без учёта факторов, связанных с конечной скоростью движения рабочего тела, особенностью теплообмена в движущемся потоке и использованием в анализах и расчётах изоэнтропно заторможенных параметров, термодинамический анализ становится неполным и не отражает общих закономерностей преобразования энергии.

В курсах по теплотехнике [1, 6] имеются разделы, посвящённые течению газов, однако в них излагаются главным образом идеально-адиабатические процессы, по существу являющиеся предметом газовой динамики. Специфические же вопросы термодинамики — это преобразование располагаемой работы в адиабатном процессе во внутреннюю теплоту в открытых системах, возникающую из-за взаимодействия газодинамических сопротивлений в канале с потоком рабочего тела, не затрагиваются или затрагиваются в минимальном объёме.

В связи с этим раздел термодинамики, посвящённый расширению рабочего тела в открытой адиабатной термодинамической системе, потеряет в значительной степени практический смысл, если не будет учитывать все воздействия, которым подвергается реальный поток.

Обнаружить последствия воздействий на поток газодинамических сопротивлений в открытой системе можно с помощью термодинамического и газодинамического анализов, то есть тепловое сопротивление, которое при обычной трактовке вопроса может рассматриваться как своеобразное явление, не требующее объяснения его физической сущности.

С учётом сказанного, на наш взгляд, для более наглядного представления результатов целесообразно вначале выполнить термодинамический анализ адиабатного процесса расширения рабочего тела в открытой системе с привлечением тепловой диаграммы в координатах T-S. Затем расширить его, с целью более углублённого обоснования преобразований в потоке, за счёт привлечения некоторых теоретических зависимостей.

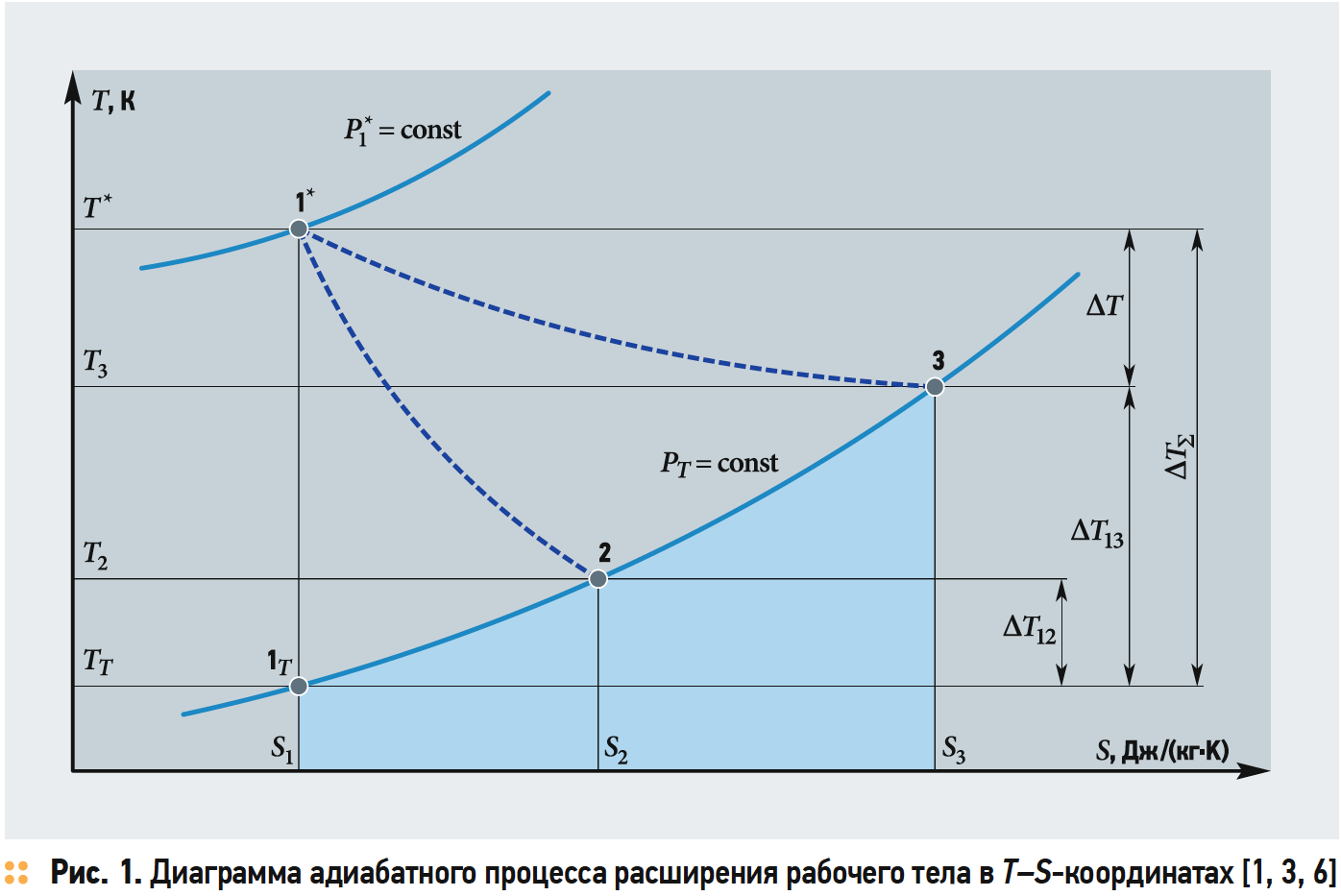
На рис. 1 и 2 представлен идеальноадиабатический процесс (то есть процесс без газодинамических потерь), который изображается вертикальными отрезками, расположенными между точками 1* и 1_T или изобарами P₁* и P_T при постоянной энтропии S₁ = const. Также показаны адиабатические процессы, которые изображаются пунктирными и прямыми отрезками 1*-2 и 1*-3 при изменяющейся энтропии ΔS ≠ 0, то есть с газодинамическими потерями.

Поскольку изобары в T-S-диаграмме имеют наклон в сторону оси абсцисс, поэтому T₃ > T₂ > T_T, и, таким образом, в процессе течения газа с потерями реализуется разность температур [(T* — T₂) или (T* — T₃)] меньшая, чем в случае обратимого идеально-адиабатического (изоэнтропного) течения без потерь при максимальном перепаде (T* — T_T) (рис. 1 и 2).

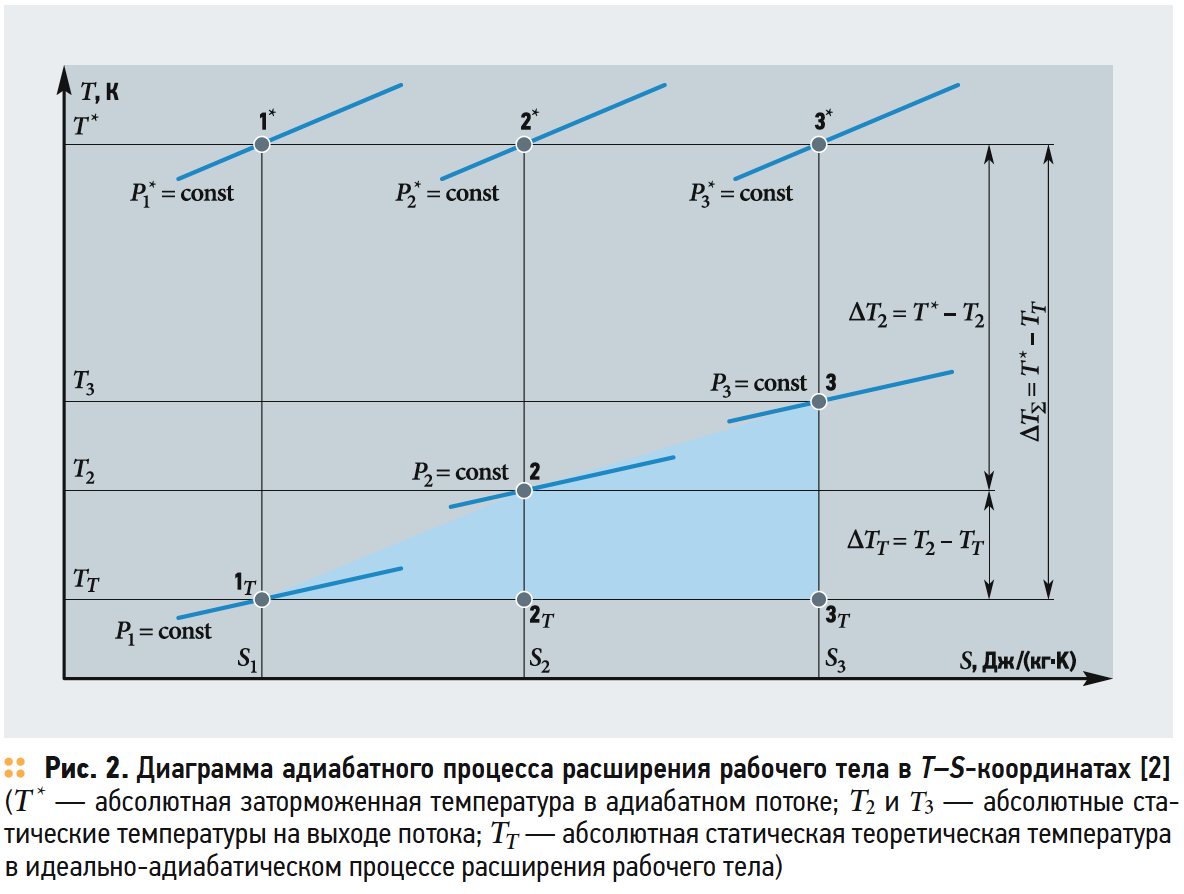
Следовательно, действительная скорость рабочего тела W_д на выходе из канала при течении с потерями будет меньше, чем теоретическая W_T при течении без потерь. В этом случае абсолютные статические температуры рабочего тела на выходе из канала при течении с потерями будут обозначены как Т₂ или Т₃.

Увеличение температур Т₂ и Т₃ относительно теоретической температуры T_T, в связи с преобразованием газодинамических потерь в теплоту, влечёт за собой увеличение произведений {Р₂V₂} или {Р₃V₃} согласно уравнению Клапейрона и, соответственно, приведёт к увеличению как статических давлений на выходе потока Р₂ или Р₃, так и удельных объёмов V₂ или V₃.

Поэтому давления Р₂ или Р₃ не должны располагаться на изобаре Р_T = const, как это представлено на диаграмме (рис. 1) [1, 3, 6], а должны перейти на другой уровень статических давлений представленных на диаграмме (рис. 2), где Р₃ > Р₂ > Р_T [2].

В связи с этим статическим температурам в движущемся потоке будет соответствовать множество удовлетворяющих состояний при соблюдении основного условия T* = const, то есть Т₂ = const, Т₃ = const и т. д.

Установить среди них то состояние, которое соответствует искомому решению, можно только с помощью другой координаты. В предельно-идеальном или теоретически возможном случае другая координата определяется из условия S₁ = S₂ = S₃ = сonst. Однако в действительном потоке энтропия возрастает, так что S₂ = S₁ + ΔS₁ или S₃ = S₁ + ΔS₂, где ΔS₁ и ΔS₂ — приращение энтропии на участке от исходного сечения до текущего.

Приращение энтропии ΔS в адиабатном потоке является не причиной, а следствием его движения, поэтому определяется только внутренними потерями, зависящими от газодинамических сопротивлений, расположенных в канале. Чем они меньше, тем меньше ΔS и тем меньше действительный процесс расширения отклоняется от изоэнтропного.

Анализируя адиабатный процесс расширения рабочего тела с потерями в открытой термодинамической системе по диаграмме T-S, выделим три характерных перепада температур ΔT_T, ΔT₂ и ΔT_Σ (рис. 1 и 2), где:

• ΔT_T = T₂ — T_T — перепад статических температур в адиабатном потоке относительно изоэнтропного уровня T_T;
• ΔT₂ = T* — T₂ — разница абсолютных заторможенной и статической температуры в адиабатном потоке;
• ΔT_Σ = T* — T_T = ΔT₂ — ΔT_T — перепад абсолютных заторможенной и теоретической температуры в изоэнтропном потоке.

В этом случае прежде всего необходимо отметить, что заторможенная температура рабочего тела в адиабатном потоке автоматически поддерживается постоянной, то есть T* = const.

Это значит, что в процессе адиабатного расширения в открытой термодинамической системе присутствует ещё и режим расширения рабочего тела при постоянной заторможенной температуре T* = const, который может быть представлен выражением P₁*V₁* = P₂*V₂*, тогда как адиабатный процесс расширения рабочего тела в открытой системе представляется совсем другой зависимостью: P₁*V₁*^m = P₂*V₂*^m, где 1 * и 2 — удельные объёмы на входе и выходе потока; m — показатель адиабатного процесса расширения рабочего тела.

Если решить эти уравнения совместно, то получим те же зависимости, которые уже имеем. Однако в этом случае появляется возможность определить элементарное количество теплоты, но только от одного механического взаимодействия газодинамических сопротивлений с потоком с учётом уравнения состояния при T* = const.

Тогда элементарное количество теплоты, образующееся в процессе расширения реального рабочего тела при постоянной заторможенной температуре в открытой термодинамической системе, будет равно как работе расширения, так и располагаемой работе, и будет выглядеть следующим образом:

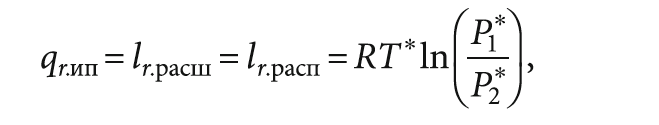
где q_r.ип — элементарное количество теплоты; l_r.расш — работа расширения; l_r.расп — располагаемая работа; P₁* — абсолютное заторможенное давление во входном сечении; P₂* — абсолютное заторможенное давление в выходном сечении; T* — абсолютная температура заторможенного потока; R — удельная газовая постоянная.

Можно считать, что краткий термодинамический анализ адиабатного процесса расширения рабочего тела в открытой системе с привлечением тепловой диаграммы в координатах T-S выполнен, но его следует расширить с целью более углублённого изучения преобразований в потоке, то есть за счёт привлечения некоторых теоретических зависимостей.

Теоретические зависимости, учитывающие газодинамические потери, вызывающие внутренний теплообмен при адиабатном расширении газа в потоке, описываются известными дифференциальными уравнениями:

Δq_r = c_vΔT + PΔV, (1)

Δq_r = c_pΔT — VΔP, (2)

Δq_r = c_aΔT, (3)

Δq_r = ξWΔW, (4)

где q_r, c_p, c_v, c_a, P, T, V, S, W и ξ — соответственно, удельная теплота газодинамических потерь, удельные теплоёмкости при постоянном давлении, объёме и адиабатного процесса, абсолютные давление и температура, удельный объём, удельная энтропия, скорость газа в потоке и коэффициент газодинамических потерь.

Совместное решение этих уравнений осуществляется с целью определения показателя адиабатного процесса расширения рабочего тела в потоке m, коэффициента газодинамических потерь ξ, удельной теплоёмкости адиабатного процесса c_a и коэффициента внутреннего теплообмена в адиабатном потоке ψ.

Решая совместно (1) и (3), а также (2) и (3), получим показатель адиабатного процесса расширения рабочего тела в открытой термодинамической системе [2–4]:

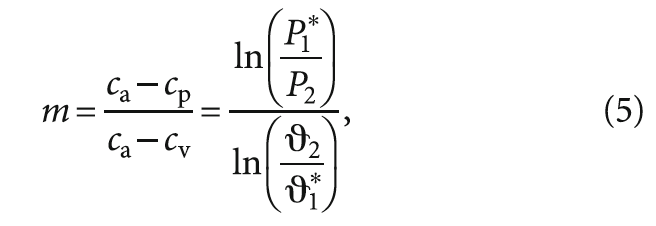
где P₁* — абсолютное давление заторможенного потока на входе в сечении 1–1; P₂ — абсолютное статическое давление в выходном сечении потока 2–2; V₁* — удельный объём, определяемый по параметрам заторможенного потока в сечении 1–1; V₂ — удельный объём, определяемый по статическим параметрам потока в сечении 2–2; m — показатель адиабатного процесса расширения рабочего тела в потоке. Кроме этого, равнозначный показатель m можно получить и другими путями, которые приведены в литературных источниках [1–5]:

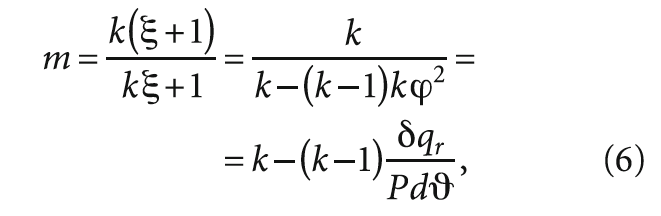
где ξ — коэффициент газодинамических потерь; k — показатель изоэнтропного процесса в открытой системе; — коэффициент скорости; Δq_r — элементарное количество теплоты, образовавшейся в потоке за счёт преобразования газодинамических потерь; ΔV — работа расширения рабочего тела.

Обозначим Δq_r/(PΔV) = ψ, где ψ — коэффициент внутреннего теплообмена в адиабатном потоке. Тогда выражение (6) будет выглядеть так: m = k — (k — 1)ψ.

Используя выражения (1–6), после несложных преобразований получим:

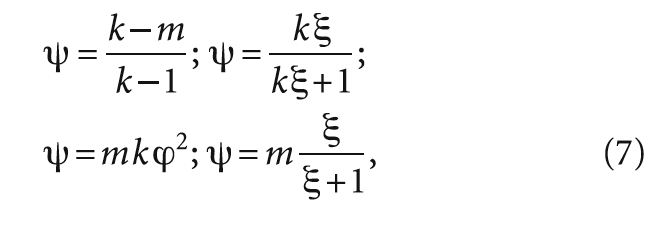
а также:

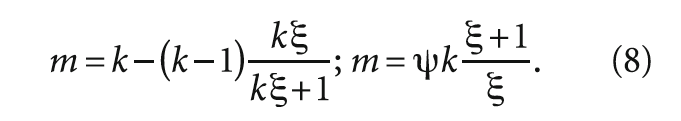
Статическую теоретически достижимую температуру в адиабатном потоке T_T определим по выражению, приведённому в [2], с использованием термических параметров потока (рис. 2) ξ = ΔT_T/ΔT, откуда после преобразования будем иметь:

T_T = T₂ — ξΔT = (ξ + 1)T₂ — ξT*, (9)

причём в данной формуле:

• T* — температура заторможенного потока;
• ΔТ = T* — T₂ — перепад заторможенной и статической температур в адиабатном потоке.

Кроме того, коэффициент газодинамических потерь ξ можно определить с использованием показателя адиабаты m, приведённом в [2]: Используя зависимость (5) и принимая во внимание, что cp = kcv, получим выражение для определения удельной теплоёмкости ca адиабатного процесса:

Используя зависимость (5) и принимая во внимание, что c_p = kc_v, получим выражение для определения удельной теплоёмкости ca адиабатного процесса:

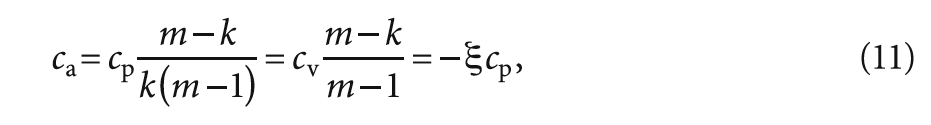
где c_p — удельная теплоёмкость при постоянном давлении; c_v — удельная теплоёмкость при постоянном объёме.

Увеличение абсолютной температуры T₂ и T₃ в адиабатном процессе расширения рабочего тела относительно её изоэнтропного уровня T_T вызвано наличием газодинамических потерь, которые, преобразуясь, увеличивают внутреннюю энергию, и определяют её суммарную необратимую часть в адиабатном потоке.

Анализируя изменения показателей адиабатного m и изоэнтропного k процессов расширения рабочего тела в открытой системе, а также коэффициентов газодинамических потерь ξ, удельной теплоёмкости c_a и коэффициента внутреннего теплообмена ψ в адиабатном потоке, как с помощью тепловой диаграммы в координатах T-S, так и приведённых зависимостей, говорит о том, что элементарное количество теплоты, возникающее в потоке как результат преобразования газодинамических потерь, состоит из двух составляющих — механической и термической.

Вывод

Таким образом, анализ адиабатного процесса расширения рабочего тела в открытой термодинамической системе с помощью тепловой диаграммы в T-S-координатах и приведённых зависимостей говорит о том, что рост изменения энтропии ΔS обеспечивается за счёт роста количества теплоты, образующегося в результате преобразования механической энергии в потоке в теплоту (отрывные течения и др.), которая усваивается текущим рабочим телом. За счёт этого увеличиваются статические параметры в выходном сечении потока и возникает дополнительное термическое сопротивление (рис. 2).