|
Такие потери пропорциональны динамическому давлению pд = ρv2/2, где ρ — плотность воздуха, равная примерно 1,2 кг/м3 при температуре около +20 °C, а v — его скорость [м/с], как правило, за сопротивлением. Коэффициенты пропорциональности ζ, называемые коэффициентами местного сопротивления (КМС), для различных элементов систем В и КВ обычно определяются по таблицам, имеющимся, в частности, в [2] и в ряде других источников. Наибольшую сложность при этом чаще всего вызывает поиск КМС для тройников или узлов ответвлений, поскольку в этом случае необходимо принимать во внимание вид тройника (на проход или на ответвление) и режим движения воздуха (нагнетание или всасывание), а также отношение расхода воздуха в ответвлении к расходу в стволе Loʹ = Lo/Lc и площади сечения прохода к площади сечения ствола fnʹ = fn/fc. Для тройников при всасывании нужно учитывать еще и отношение площади сечения ответвления к площади сечения ствола foʹ = fo/fc. В руководстве [2] соответствующие данные приведены в табл. 22.36–22.40. Однако, при больших относительных расходах в ответвлении КМС меняются весьма резко, поэтому в этой области рассматриваемые таблицы вручную интерполируются с трудом и со значительной погрешностью. Кроме того, в случае использования электронных таблиц MS Excel опять-таки желательно иметь формулы для непосредственного вычисления КМС через отношения расходов и сечений. При этом такие формулы должны быть, с одной стороны, достаточно простыми и удобными для массового проектирования и использования в учебном процессе, но, в то же время, не должны давать погрешность, превышающую обычную точность инженерного расчета. Ранее подобная задача была решена автором применительно к сопротивлениям, встречающимся в водяных системах отопления [3]. Рассмотрим теперь данный вопрос для механических систем В и КВ. Ниже приведены результаты аппроксимации данных [2] для унифицированных тройников (узлов ответвлений) на проход. Общий вид зависимостей выбирался, исходя из физических соображений с учетом удобства пользования полученными выражениями при обеспечении допустимого отклонения от табличных данных: 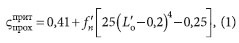 ❏ для приточных тройников, при Loʹ ≤ 0,7 и fnʹ ≥ 0,5:а при Loʹ ≤ 0,4 можно пользоваться упрощенной формулой: 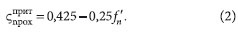 ❏ для вытяжных тройников: 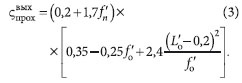 Нетрудно заметить, что относительная площадь прохода fnʹ при нагнетании или соответственно ответвления foʹ при всасывании влияет на КМС одинаковым образом, а именно с увеличением fnʹ или foʹ сопротивление будет уменьшаться, причем числовой коэффициент при указанных параметрах во всех приведенных формулах один и тот же, а именно (–0,25). Кроме того, и для приточных, и для вытяжных тройников при изменении расхода воздуха в ответвлении относительный минимум КМС имеет место при одинаковом уровне Loʹ = 0,2. Данные обстоятельства говорят о том, что полученные выражения, несмотря на свою простоту, в достаточной мере отражают общие физические закономерности, лежащие в основе влияния исследуемых параметров на потери давления в тройниках любого типа. В частности, чем больше fnʹ или foʹ, т.е. чем ближе они к единице, тем меньше меняется структура потока при прохождении сопротивления, а значит, и меньше КМС. Для величины Loʹ зависимость является более сложной, но и здесь она будет общей обоих режимов движения воздуха. Представление о степени соответствия найденных соотношений и исходных значений КМС дает рис. 1, где показаны результаты обработки таблицы 22.37 для КМС унифицированных тройников (узлов ответвлений) на проход круглого и прямоугольного сечения при нагнетании. Примерно такая же картина получается и для аппроксимации табл. 22.38 с помощью формулы (3). Заметим, что, хотя в последнем случае речь идет о круглом сечении, нетрудно убедиться, что выражение (3) достаточно удачно описывает и данные табл. 22.39, относящиеся уже к прямоугольным узлам. 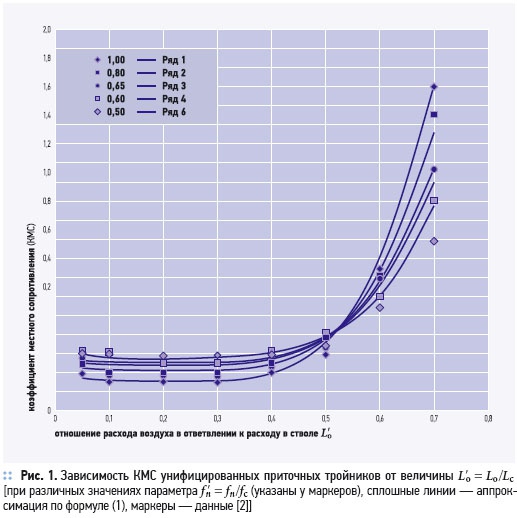 Погрешность формул для КМС в основном составляет 5–10 % (максимально до 15 %). Несколько более высокие отклонения может давать выражение (3) для тройников при всасывании, но и здесь это можно считать удовлетворительным с учетом сложности изменения сопротивления в таких элементах. Во всяком случае, характер зависимости КМС от влияющих на него факторов здесь отражается очень хорошо. При этом полученные соотношения не требуют никаких иных исходных данных, кроме уже имеющихся в таблице аэродинамического расчета. В самом деле, в ней в явном виде должны быть указаны и расходы воздуха, и сечения на текущем и на соседнем участке, входящие в перечисленные формулы. Особенно это упрощает вычисления при использовании электронных таблиц MS Excel. В то же время формулы, приведенные в настоящей работе, весьма просты, наглядны и легко доступны для инженерных расчетов, особенно в MS Excel, а также в учебном процессе. Их применение позволяет отказаться от интерполяции таблиц при сохранении точности, требуемой для инженерных расчетов, и непосредственно вычислять КМС тройников на проход при самых разнообразных соотношениях сечений и расходов воздуха в стволе и ответвлениях. Этого вполне достаточно для проектирования систем В и КВ в большинстве жилых и общественных зданий. 1. А.Д. Альтшуль, Л.С. Животовский, Л.П. Иванов. Гидравлика и аэродинамика. — М.: Стройиздат, 1987. 2. Справочник проектировщика. Внутренние санитарно-технические устройства. Ч. 3. Вентиляция и кондиционирование воздуха. Кн. 2 / Под ред. Н.Н. Павлова и Ю.И. Шиллера. — М.: Стройиздат, 1992. 3. О.Д. Самарин. О расчете потерь давления в элементах систем водяного отопления // Журнал С.О.К., №2/2007. |
  |
Расчет местных сопротивлений в системах вентиляции
Опубликовано в журнале СОК №2 | 2012
Rubric:
Тэги:
Как известно [1], при движении воздушного потока в системах вентиляции и кондиционирования воздуха (В и КВ), кроме потерь давления на трение, большую роль играют потери на местных сопротивлениях — фасонных частях воздуховодов, воздухораспределителях и сетевом оборудовании.

























