
Во многих населённых пунктах России периодически наблюдаются аномальные зимние погодные условия, включающие в себя резкое увеличение скорости ветра. Классическим примером таких аномалий является «бора» в городе Новороссийск — сильный ветер северо-восточного направления, достигающий скорости в порывах до 80 м/с, и одновременное резкое понижение температуры воздуха в холодный период года. Продолжительность боры — от суток до недели. Суточный перепад температур во время боры в этот период может достигать 40°C [1, 2].
Энергетически эффективное поддержание комфортных условий микроклимата в обитаемых помещениях, как при расчётных погодных условиях, так и в период таких аномалий, в соответствии с требованиями технических регламентов [3], обеспечивается путём создания достаточно высокого термического сопротивления конструкции наружных стен. Даже если исключить возникновение аварий в системах электроснабжения, вызванных аномальными явлениями, продолжительные изменения внешних условий теплообмена могут обусловить снижение температуры на внутренней поверхности стен и результирующей температуры, нормирование которой определено Федеральным законом №384-ФЗ [4]. Для обеспечения энергетически эффективного и экономичного термического сопротивления строительных конструкций наружных стен применяются многослойные конструкции, один из слоёв которых предназначен для создания «барьера» при распространении теплового потока. Целью настоящей работы является разработка методики и анализ результатов решения задачи нестационарной теплопроводности в многослойной стене здания при аномальных зимних погодных условиях в городе Новороссийске.
Рассмотрим теплофизические особенности процесса теплообмена в многослойной стене в общей постановке.
Расчёт произведём без учёта фазовых превращений и зависимостей теплофизических характеристик сопряжённых слоёв в зависимости от температуры. Многослойная стена в условиях одномерности описания процессов теплопередачи в рассматриваемой в статье задаче моделируется пятислойной: первый слой — керамический поверхностный слой: второй — теплоизоляционный слой, третий — слой, обеспечивающий прочность конструкции; четвёртый и пятый слои — неметаллические слои, обеспечивающие выравнивание и декорирование внутренней поверхности стены помещения.
Изменение температуры по сечению (вдоль координаты х) в любой момент времени для каждого слоя многослойной стены определяется из решения системы дифференциальных уравнений в частных производных:
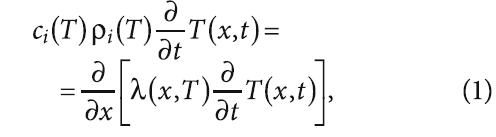
где i — индекс, определяющий принадлежность параметров к различным слоям многослойной стены; ci(T) — удельная теплоёмкость материала i-го слоя как функция температуры; ρi(T) — плотность материала i-го слоя как функция температуры; λ(x,T) — коэффициент теплопроводности материала как функция температуры T и координаты x, направленной по нормали к поверхности стены.
Условия теплового сопряжения на границах слоёв имеют вид:
x = xi, Ti = Ti-1,
что соответствует условию неразрывности функции температуры.

Выбор граничных условий для рассматриваемой постановки задачи предлагается сделать из следующих условий. На внешней поверхности многослойной стены происходит конвективный теплообмен при переменных во времени значениях температуры атмосферного воздуха и коэффициента теплоотдачи, который описывается аналогично граничному условию III рода:
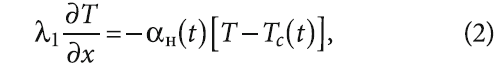
где αн(t) — коэффициент теплоотдачи от наружной поверхности стены; Tc(t) — температура атмосферного воздуха.
Суточный ход температуры атмосферного воздуха в период боры имеет общие закономерности, такие как резкое снижение в первые сутки, суточные колебания и т. п., и зависит от многих факторов. В качестве исходных данных примем задокументированные атмосферные процессы конца января — начала февраля 2012 года [1].
Измеренные значения температуры атмосферного воздуха в период с 24 февраля 2012 года представлены на рис. 1а.
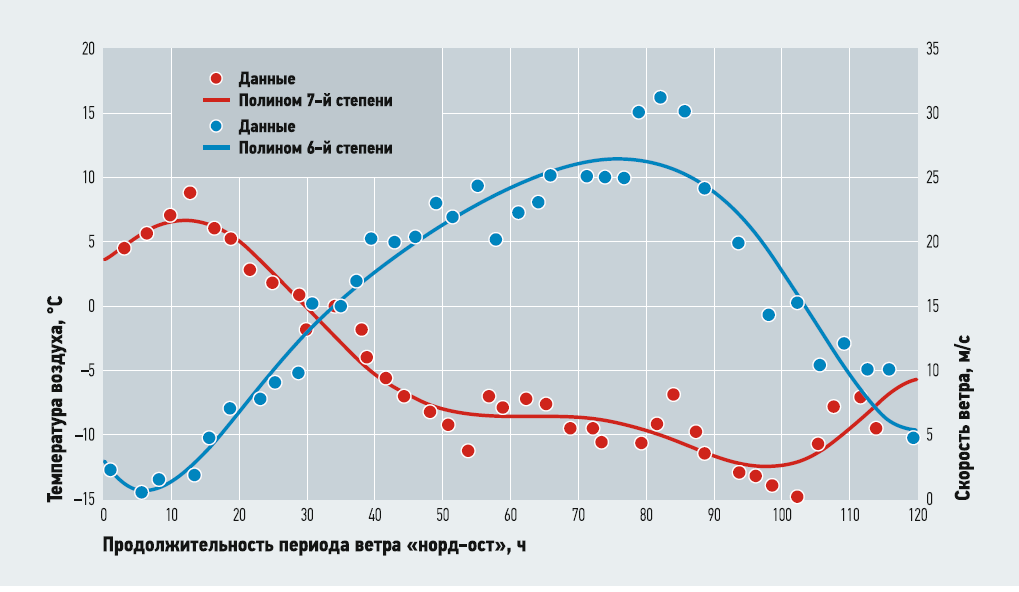
Рис. 1. Измеренные значения (а — атмосферной температуры, б — скорости ветра)
Принятые на рис. 1а обозначения таковы: треугольные маркёры обозначают измеренное значение температуры атмосферного воздуха (нулевая ордината соответствует времени 00:00 на 24 февраля); сплошная линия соответствует полиному седьмой степени, аппроксимирующему эти значения и имеющему вид:

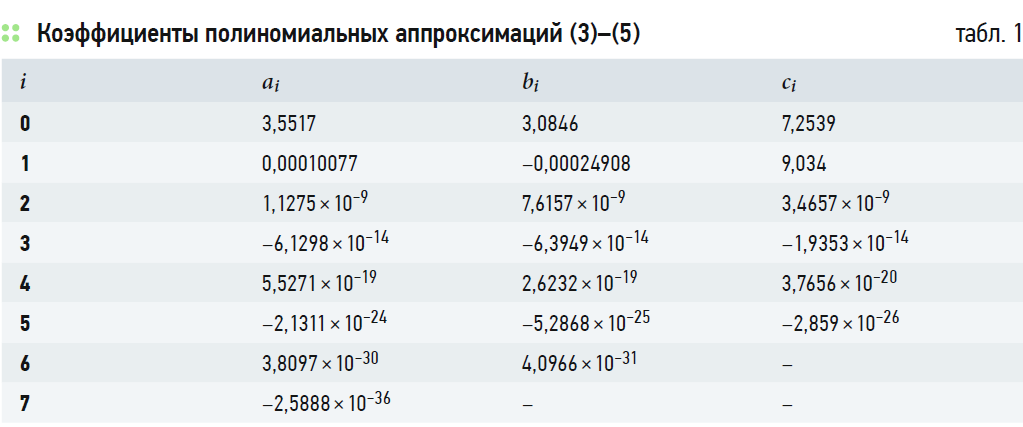
Коэффициенты полинома седьмой степени, полученные по результатам обработки данных рис. 1а, для значений времени [секунды], представлены во втором столбце табл. 1 «Коэффициенты полиномиальных аппроксимаций (3)-(5)».
Измеренные значения скорости ветра в период с 24 февраля показаны на рис. 1б. Принятые на рис. 2б обозначения: треугольные маркёры показывают измеренное значение скорости ветра (нулевая ордината соответствует времени 00:00 на 24 февраля); сплошная линия соответствует полиному шестой степени, аппроксимирующему эти значения и имеющему следующий вид:
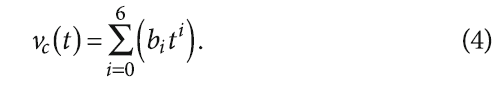
Коэффициенты полинома шестой степени, полученные по результатам обработки данных рис. 1б, для значений времени, выраженных в секундах, представлены в третьем столбце табл. 1.
Коэффициент теплоотдачи от наружной поверхности стены также зависит от скорости ветра и может быть определён по формуле Франка [5]:
αн = 7,34v0,656 + 3,78e-1,91v,
где αн — коэффициент теплоотдачи от наружной поверхности стены, Вт/( м²·°C); v — скорость ветра, м/c.
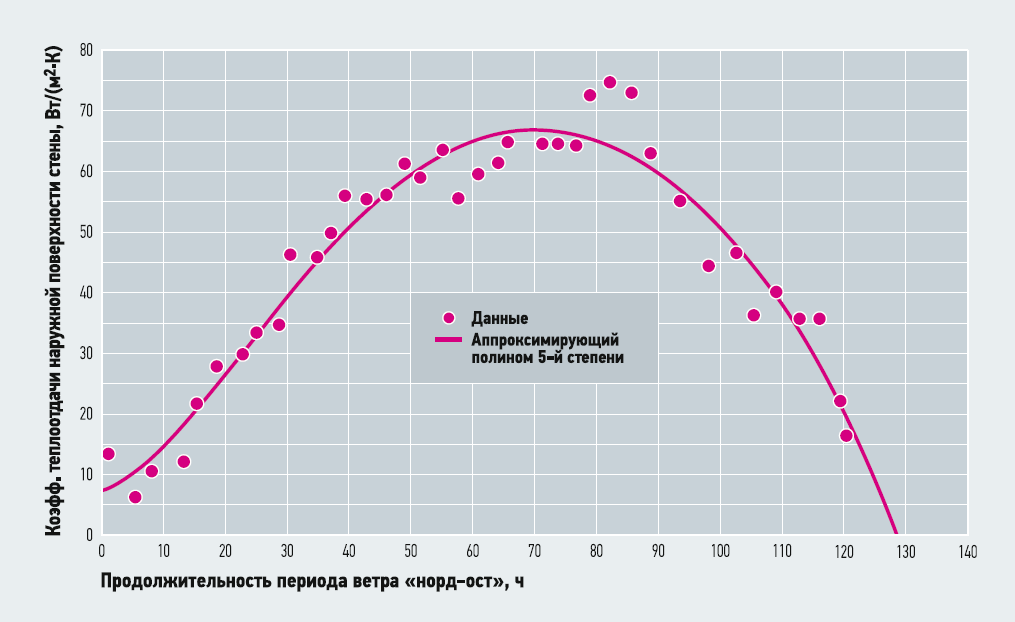
Рис. 2. Коэффициент теплоотдачи от наружной стены
График изменения (в период «норд-оста») рассчитанных по этой формуле значений коэффициента теплоотдачи от наружной поверхности стены показан на рис. 2. Принятые на рис. 2 обозначения: треугольные маркёры показывают измеренное значение скорости ветра, (нулевая ордината соответствует времени 00:00 на 24 февраля); сплошная линия соответствует полиному пятой степени, аппроксимирующему эти значения:
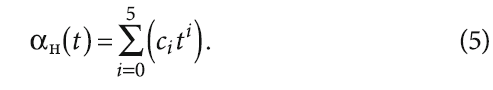
Коэффициенты полинома пятой степени, полученные по результатам обработки данных рис. 2, для значений времени, выраженных в секундах, представлены в четвёртом столбце табл. 1.
Будем считать, что на внутренней поверхности многослойной стены происходит конвективный теплообмен при постоянных во времени значениях температуры воздуха и величин коэффициента теплоотдачи:
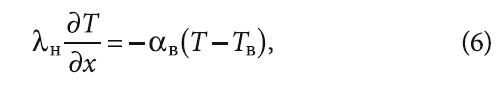
где αв — коэффициент теплоотдачи от внутренней поверхности стены; Tв — температура воздуха внутри помещения.
Величина коэффициента αв, в соответствии с рекомендациями [3], принята равной 8,7 Вт/( м²·°C).
Для решения задачи нестационарной теплопроводности могут использоваться разнообразные численные методы [6]. Для решения задач со сложными, изменяющимися во времени граничными условиями можно весьма эффективно использовать метод прямых [7].
В качестве примера исходных данных для решения рассматриваемой задачи используем параметры конструкции внешней стены жилого коттеджа, состоящей из четырёх слоёв строительных материалов (пятый слой объединён с четвёртым ввиду незначительности его толщины и схожести теплофизических характеристик), свойства которых представлены в табл. 2.
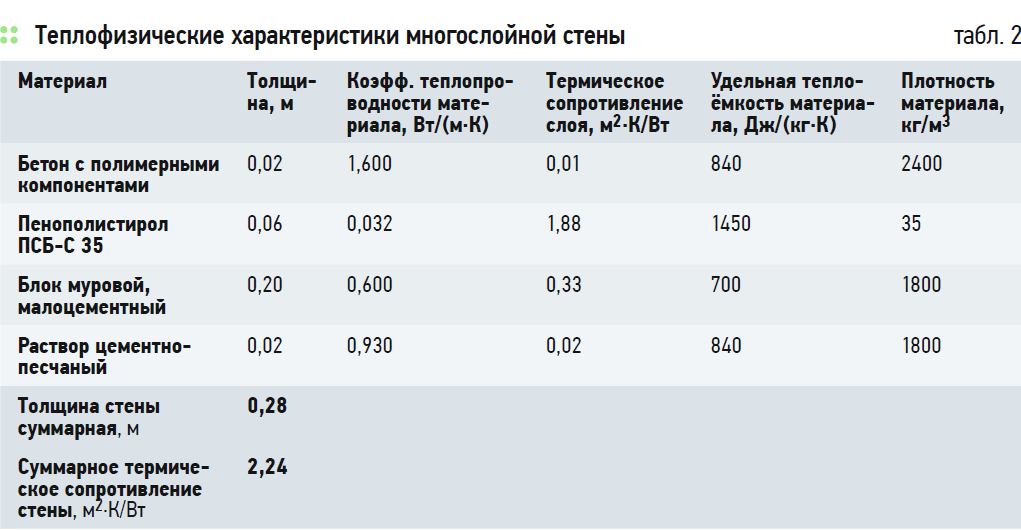
В качестве начальных условий примем стационарное распределение температуры по толщине данной стены в момент времени 23:00 на 23 февраля 2012 года, когда были зарегистрированы T0с = 4°C и T0в = 20°C.
Дискретизацию уравнения (1), в соответствии с методом прямых, в точках, отличных от граничных, произведём с использованием центрально-разностной схемы второго порядка для вторых производных, имеющей вид:
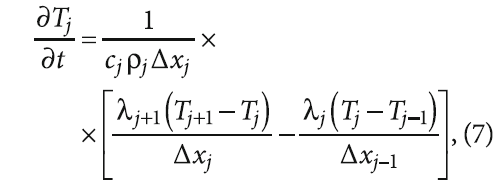
где Tj, cj, ρj и λj — температура, теплоёмкость, плотность и коэффициент теплопроводности в j-й точке дискретного разбиения слоёв конструкции стены, соответственно; Δxj — расстояние между двумя соседними точками.
Для обеспечения порядка аппроксимации первой производной, не меньшего, чем порядок аппроксимации для точек, отличных от граничных, дискретизацию уравнения (2) на внешней поверхности стены произведём с использованием разностной схемы второго порядка для первой производной с разностями вперёд, что имеет вид:
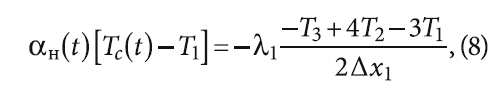
и после преобразований получим значение температуры для внешнего поверхностного слоя:
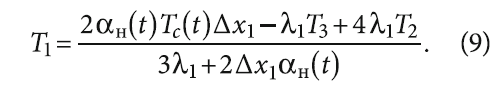
Аналогично, дискретизацию уравнения (6) на внутренней поверхности стены произведём с использованием разностной схемы для первой производной второго порядка с разностями назад, что имеет следующий вид:

и после преобразований получим значение температуры для внутреннего поверхностного слоя стены:
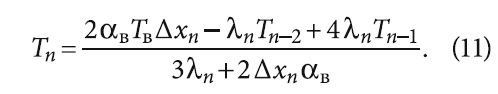
Для обеспечения порядка аппроксимации второй производной не меньшего, чем порядок аппроксимации для точек, отличных от граничных, дискретизацию уравнения (1) можно произвести, используя четырёхточечные формулы [8] с разностями вперёд для первого слоя:
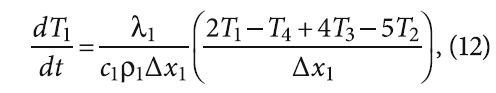
и аналогичные с разностями назад для последнего слоя стены:
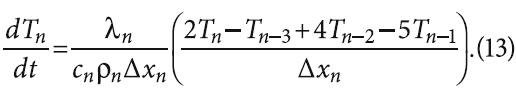
Для решения рассматриваемой задачи нестационарной теплопроводности в многослойной стене здания каждый слой теплоизоляции был разбит на десять отрезков равной величины по каждому слою, и составлена программа, реализующая систему из дифференциальных уравнений (7)-(13) в программной среде MATLAB. Решение системы дифференциальных уравнений (7)-(13) осуществлялось с помощью численных методов Рунге-Кутты с автоматическим выбором шага при помощи встроенной функции.
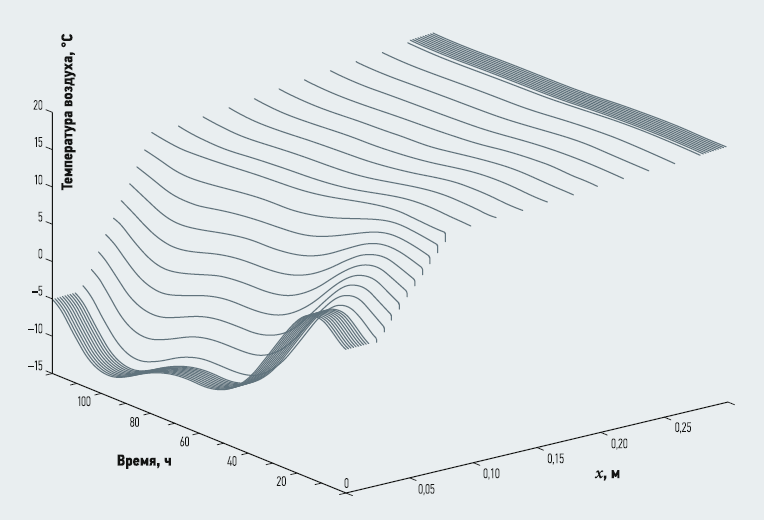
Рис. 3. График изменения температуры по толщине стены в течение погодной аномалии
Результаты решения для исходных данных, представленных в табл. 1, показаны в графическом виде на рис. 3 и 4.
Представленная на рис. 4 серая прямая линия соответствует значению мощности теплового потока от внутренней поверхности стены для расчётных условий стационарной теплопроводности, нормируемых в соответствии с требованиями СП 50.13330.2012 [3], а зелёная прямая линия соответствует тепловому потоку в начальный момент времени до возникновения погодной аномалии.
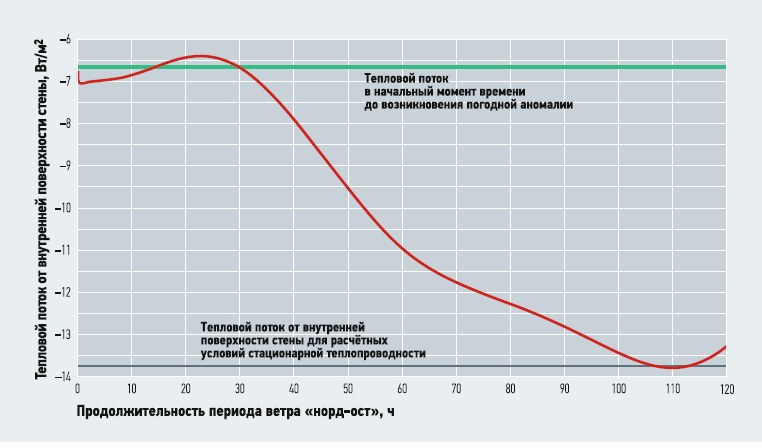
Рис. 4. График изменения мощности теплового потока у внутренней поверхности стены
Выводы
Из анализа представленных графиков можно сделать следующие выводы. Наличие «барьерного» слоя теплоизоляции стены существенно снижает амплитуду колебаний температуры. Значение мощности теплового потока от внутренней поверхности стены к концу периода погодной аномалии превышает значение мощности, рассчитанное для условий стационарной теплопроводности, в соответствии с требованиями СП 50.13330.2012 [3], что требует создания соответствующего запаса мощности теплогенераторов и отопительных приборов для поддержания комфортных условий в обитаемых помещениях.


























