Если в воду добавить, предположим, хлорид натрия (NaCl), то в воде данная соль диссоциирует на катион Na+ и анион Cl-. Получив электромагнитное поле, данная соль сможет переносить электрический заряд. В воде будет наблюдаться ионная проводимость, то есть электрический заряд будет перемещаться за счёт перемещения ионов Na и Cl.
По теории Дебая — Хюккеля предполагается, что в воде вокруг каждого катиона образуется сфера из анионов и, соответственно, вокруг каждого аниона образуется сфера из катионов. Предполагая, что каждый ион можно представить как точечный заряд, распределение ионов в воде на плоскости можно представить следующим образом — рис. 1. Ионы образуют шестиугольник, в вершинах которого чередуются катионы и анионы. Тогда вокруг каждого катиона образуется сфера из равноудалённых анионов и наоборот. Но это в случае предположения, что ион является точечным зарядом.
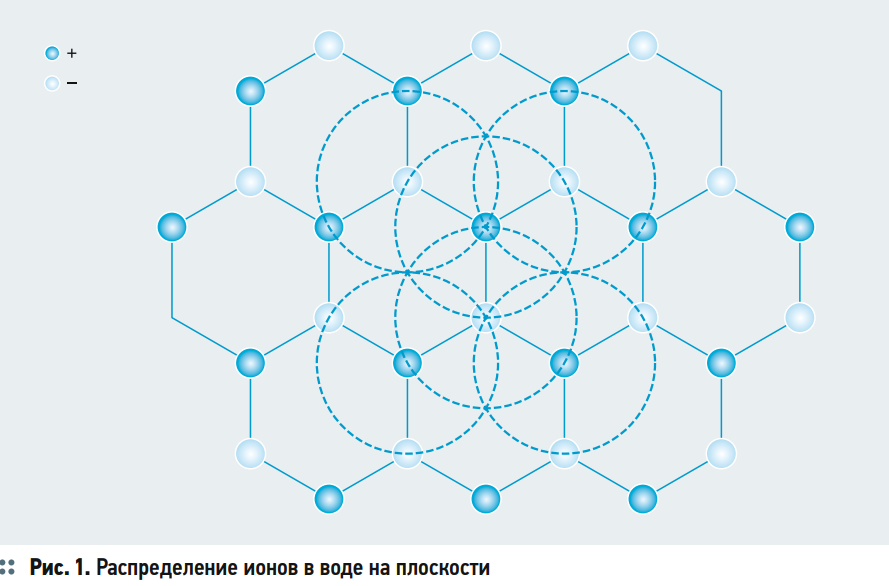
Но как быть, если в воде присутствуют двухвалентные ионы, и как учитывать разные размеры иона? К примеру, в сульфат-анионе содержатся четыре атома кислорода и один атом серы. Тем не менее считается, что теория Дебая — Хюккеля вполне применима для расчёта значений удельной электропроводности растворов для небольших концентраций.
В соответствии с данной теорией, для того чтобы уйти от понятия «точечного заряда» и прийти к ионам, предполагается, что ионы имеют некое значение эквивалентной электропроводности при бесконечном разбавлении. В физическом смысле это означает, что если в воде присутствует только, предположим, катион натрия, и на него не оказывается воздействие других ионов, то этот катион в эквивалентной концентрации может перенести определённое количество электрического заряда. Это предположение или допущение, по сути, крайне спорно, поскольку в воде не могут быть по отдельности только катионы или анионы. Правильнее сказать, что возможности по переносу электрического заряда катионом определяются его анионом и наоборот.
По сути, вся теория работает только для электролитов валентностей 1–1, где ионы с определённым допущением могут быть представлены как точечный заряд.

Рассмотрим пример.
Автору по своей работе необходимо заниматься контролем водно-химических режимов котельных с различными способами водоподготовки. Самый распространённый метод водоподготовки — это Na-катионитовое умягчение воды. В результате поиска средств дистанционного контроля подобных установок было выяснено, что для пресной воды электропроводность умягчённой воды практически всегда больше электропроводности исходной жёсткой воды. При этом существующая теория утверждает обратное.
В патенте [1] используется условие, что электропроводность умягчённой воды в среднем на 5% больше электропроводности исходной воды. Это исключает научную ценность, но делает данную работу ресурсным источником для рассуждений и последующего выявления факторов и закономерностей, определяющих данное поведение ионов в водном растворе.
Действительно, как будет показано далее, для пресных кальциево-магниевых-гидрокарбонатных вод в среднем электропроводность умягчённой воды на 5% выше электропроводности исходной жёсткой воды. Для воды с другим ионным составом процент перепада может значительно отличаться.
Вернёмся к примеру. Имеется исходная вода следующего ионного состава:
1. Катионы: Ca = 2,0 мг-экв/л; Mg = 1,2 и Na = 0,78 мг-экв/л.
2. Анионы: HCO3 = 1,9 мг-экв/л; SO4 = 1,44 и Cl = 0,64 мг-экв/л.
Итого К = А = 3,98 мг-экв/л. Измеренная электропроводность данной воды составила 409 мкСм/см.
Произведём расчёт значения электропроводности, используя значения электропроводностей каждого иона в зависимости от их общей концентрации в воде. Значения электропроводности ионов от их концентраций представлены в [2].
В результате простого сложения электропроводности отдельного иона, в зависимости от его концентрации, получаем значение удельной электропроводности воды, равное 429 мкСм/см.
Затем мы рассчитаем электропроводность полностью умягчённой воды. В этом случае в качестве катионов существуют только катионы натрия. То есть Na = 3,98 мг-экв/л. Расчётная электропроводность умягчённой воды получается равной 418 мкСм/см.
Получается, что электропроводность исходной воды больше электропроводности умягчённой воды, что неверно.
В разных источниках значения электропроводности ионов от их концентрации могут немного отличаться, но принципиально это не оказывает влияния на результат расчёта. Электропроводность исходной воды всегда больше электропроводности умягчённой воды, что не подтверждается на практике.
Такая ситуация возникает из-за того, что недопустимо наделять ион неким одним значением эквивалентной электропроводности при бесконечном разбавлении, поскольку это значение будет различное для солей валентностей 1–1 и 2–2.
Каким образом получены значения эквивалентной электропроводности при бесконечном разбавлении?
Рассмотрим две соли 1–1: KCl и NaCl.
При диссоциации в воде возникают соответствующие ионы.
Затем делается предположение, что если бы в воде существовали только катионы этой соли, какая бы была величина её электропроводности и, соответственно, какая была бы величина электропроводности, если бы в воде существовали только анионы. Затем определяется среднее значение электропроводности и делится на два.
Для того чтобы реализовать это условие, вводится понятие чисел переноса.
Числа переноса говорят о том, какая доля электрического заряда переносится катионом и, соответственно, какая анионом. То есть:
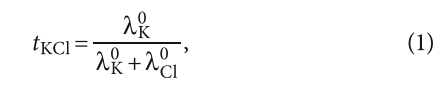
где tKCl — число переноса для KCl; λK0 — эквивалентная электропроводность калия при бесконечном разбавлении; λCl0 — эквивалентная электропроводность хлорида при бесконечном разбавлении. Соответственно, λCl0 = 1 — λK0.
Также:
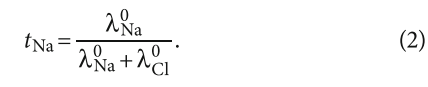
В табл. 1 приведены данные по эквивалентной электропроводности хлорида кальция и натрия при различных мольных концентрациях.
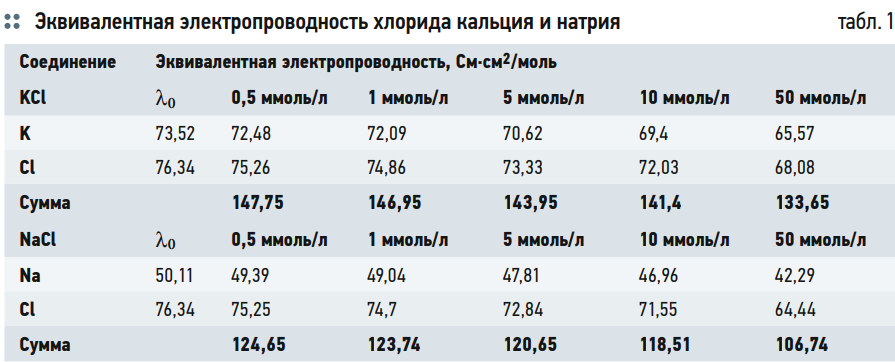
В строке «сумма» указана эквивалентная электропроводность соответствующей соли при соответствующей концентрации. Так, при концентрации раствора 1 ммоль/л значения 146,95 для KCl и 123,74 для NaCl будут равны измеренным значениям в мкСм/см. Соответственно, можно экспериментально получить значения эквивалентных электропроводностей для обеих солей.
В табл. 1 во втором столбце сразу указан результат интерполяции по обнаружению значений эквивалентной электропроводности ионов при бесконечном разбавлении.
Таким образом:
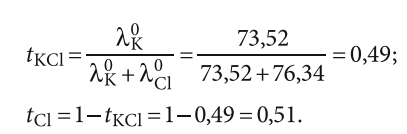
Получается, что калий и хлорид переносят почти одинаковую долю электричества.
Для концентрации 0,5 ммоль/л KCl:
- К = 0,49×147,75 = 72,48;
- Сl = 0,51×147,75 = 75,26,
здесь погрешность в расчётах из-за округления до второго знака после запятой, а 147,75 — значение, полученное экспериментально.
Для NaCl:
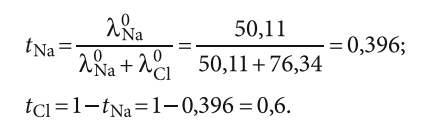
Для концентрации 0,5 ммоль/л NaCl:
- Na = 0,396×124,65 = 49,39;
- Cl = 0,6×124,65 = 75,25;
- сумма: 49,39 + 75,25 = 124,65.
Получается, что определённое при помощи чисел переноса и изначально заданных значениях эквивалентной электропроводности ионов при бесконечном разбавлении значение эквивалентной электропроводности раствора NaCl при концентрации 0,5 ммоль/л равно экспериментально полученному значению при этой концентрации.
Равенство рассчитанных значений при помощи чисел переноса и ионов при бесконечном разбавлении и полученных экспериментально действительно подтверждает возможность использования такого понятия, как эквивалентная проводимость иона при бесконечном разбавлении.
Но, к сожалению, данная концепция работает только для 1–1 электролитов, где действительно во многом выполняются допущения, принятые в теории Дебая — Хюккеля.
Если мы возьмём соль 2–1 или тем более 2–2, то невозможно подбором, интерполяцией или т. п. определить единственное значение эквивалентной электропроводности иона при бесконечном разбавлении, которое бы подходило для солей различной валентности. К примеру, значение эквивалентной электропроводности сульфата при бесконечном растворении в соединении с натрием 2–1 будет значительно отличаться от того же значения в соединении сульфата с магнием 2–2. Это говорит о том, что значение эквивалентной электропроводности отдельного иона при бесконечном разбавлении не является базовой физической величиной и не может использоваться в расчётах растворов с ионами различной валентности. Фактически это находит применение только для расчётов солей 1–1.
Именно поэтому расчёт по ионам показывает, что умягчённая природная вода при малых концентрациях имеет меньшее значение электропроводности, чем исходная. Что неверно, так как природная вода содержит различные типы ионов, в том числе двухвалентные, что делает невозможным применение такого понятия, как «эквивалентная проводимость отдельного иона при бесконечном разбавлении».

Необходимо говорить о том, что физический смысл имеет только значение эквивалентной электропроводности соли, поскольку катион и анион непрерывно связаны, и свойства одного зависят от свойств другого. При этом, заменяя катион или анион, в паре меняются и свойства оставшегося иона — по крайней мере, в способности в переносе электрического заряда, что вызвано подвижностью иона. Если анион менее подвижен, это отражается и на катионе. Хотя прямой зависимости при этом не наблюдается.
Попробуем, зная экспериментальные данные по эквивалентным электропроводностям солей, рассчитать значение электропроводности водного раствора ионов различных валентностей.
В исходной воде нашего примера содержится шесть ионов. Соответственно, в воде могут быть образованы девять типов солей:
- Ca(HCO3)2, CaCl2, Mg(HCO3)2, MgCl2, Na2SO4 — соли 2–1;
- СaSO4, MgSO4 — соли 2–2;
- NaHCO3, NaCl — соли 1–1.
Возникает вопрос, каким образом определить концентрацию каждой соли в воде.
Можно использовать тот факт, что электропроводность всего исследуемого конечного объёма воды одинакова. То есть, если мы возьмём (выделим) небольшой объём воды из изначального конечного объёма, то электропроводности этих объёмов воды будут одинаковы. Можно сделать вывод, что ионы распределяются в объёме воды равномерно с учётом их валентностей.
Видимо, существует принцип, который можно сформулировать следующим образом. Концентрации в мг-экв/л и соотношение концентраций катионов и анионов в исходном объёме воды равны концентрации и соотношению концентраций катионов и анионов в любом выделенном меньшем объёме воды из исходного объёма воды.
Данный принцип равномерности можно записать следующим образом для определения концентрации конкретной соли:
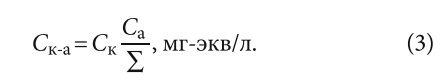
где Ск-а — концентрация соответствующей соли, мг-экв/л; Cк — концентрация соответствующего катиона, мг-экв/л; Cа — концентрация соответствующего аниона, мг-экв/л; Σ = ΣCк = ΣCа — сумма катионов, равная сумме анионов, взятых в мг-экв/л.
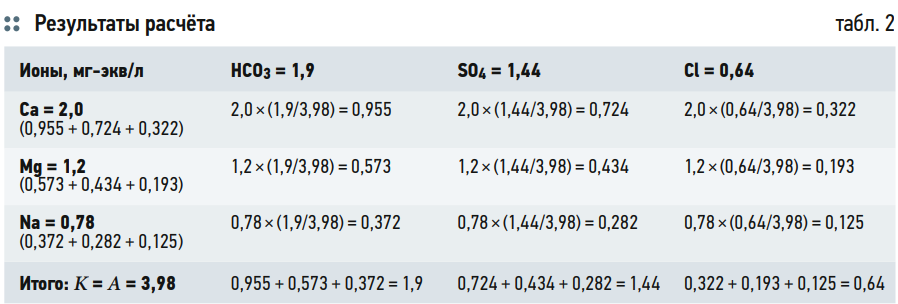
В табл. 2 представлен расчёт концентраций солей, содержащихся в исходной воде в соответствии с концентрациями ионов. То есть общее количество катионов или анионов равно 3,98 мг-экв/л. При этом доля бикарбоната в анионной части составляет 1,9/3,98 = 0,477.
Соответственно:
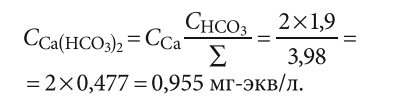
Таким же образом производится расчёт для всех девяти солей. Результаты расчёта сведены в табл. 2. Получаем:
- Ca(HCO3)2 = 0,955 мг-экв/л;
- CaSO4 = 0,724 мг-экв/л;
- СаCl2 = 0,322 мг-экв/л.
- Mg(HCO3)2 = 0,573 мг-экв/л;
- MgSO4 = 0,434 мг-экв/л;
- MgCl2 = 0,193 мг-экв/л;
- NaHCO3 = 0,372 мг-экв/л;
- Na2SO4 = 0,282 мг-экв/л;
- NaCl = 0,125 мг-экв/л.
В результате в начале расчёта, имея только химический анализ по концентрации отдельных ионов, мы получаем значения концентрации всех образующихся в воде солей.
Теперь, используя методику чисел переноса, можно определить значение электропроводности воды исходя из значений электропроводности отдельных солей (а не отдельных ионов). Для этого были использованы данные источника [3].
Поскольку расчёт эквивалентных электропроводностей солей 2–2 по предлагаемой в [3] методике невозможен, то автором был произведён эксперимент по определению эквивалентных электропроводностей для сульфата магния в зависимости от концентрации.
В результате более или менее допустимая аппроксимация полученных данных получилась только до диапазона концентраций MgSO4 до 5 ммоль/л из-за того, что данная соль активно создаёт ионные пары при увеличении концентрации. При более высоких концентрациях для расчёта необходимо вручную использовать массив данных либо проводить более сложную аппроксимацию.
Данные для CaSO4 были взяты, предполагая поведение кальция по отношению к сульфату, как в соединениях CaCl2 и MgCl2.
В результате были получены уравнения зависимостей значений электропроводности от концентраций для всех девяти солей.
Далее была использована методика чисел переноса. Были рассчитаны значения электропроводностей для каждой из девяти солей при условии, что в воде содержится только эта соль. При этом мольная концентрация этой соли соответствует мольной концентрации всех девяти солей.
Затем полученная концентрация каждой соли умножалась на её реальную мольную концентрацию. В результате были получены значения электропроводности каждой соли при её «реальной» концентрации. Затем данные значения суммируются и получается значение удельной электропроводности водного раствора.
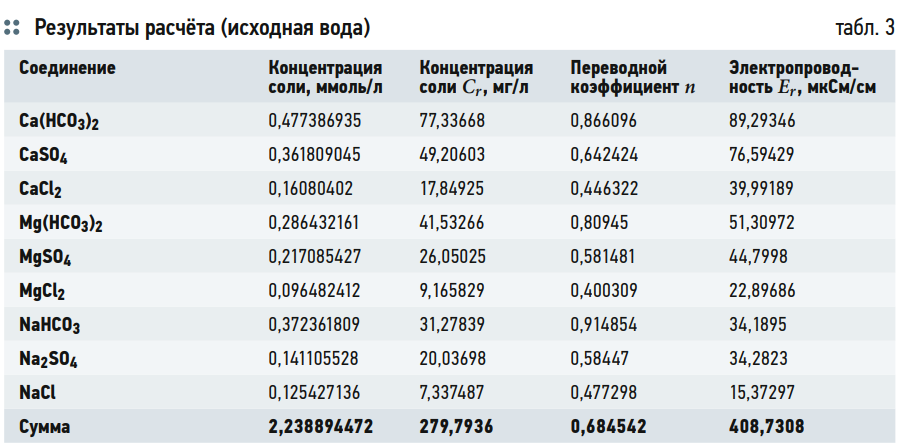
Результаты расчёта представлены в табл. 3 и 4. В табл. 3 представлен расчёт суммарной мольной концентрации солей в исходной воде, а также расчёт электропроводности каждой соли и расчёт суммарной электропроводности исходной воды. В табл. 4 представлен результат расчёта электропроводности каждой соли в зависимости от суммарной мольной концентрации водного раствора.
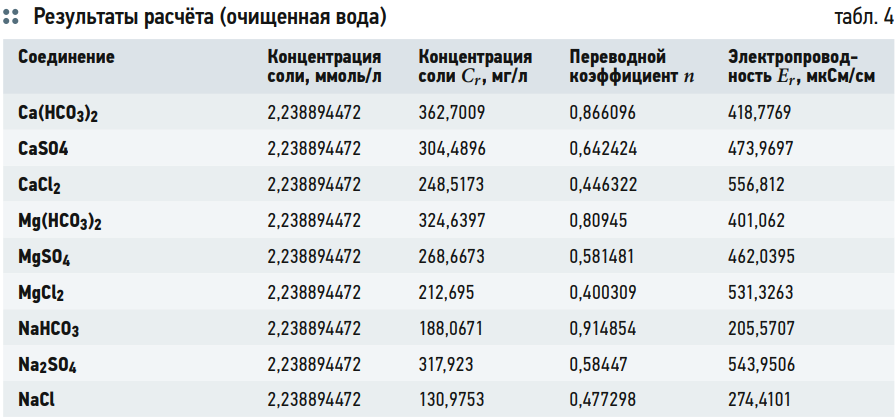
Вначале определяется общая мольная концентрация солей в воде (табл. 3, второй столбец). Затем, предполагая, что в воде содержится только соль одного типа с такой концентрацией, рассчитываем значение электропроводности данной соли при общей мольной концентрации всех солей (табл. 4, столбец 5). Для расчёта используются экспериментально полученные данные для конкретного типа соли. Далее рассчитывается величина переводного коэффициента:
n = C/E,
где С — концентрация соответствующей соли в мг/л; Е — электропроводность той же соли.
Затем в табл. 3 значение в столбце 3 (Cr) делится на соответствующее каждой соли значение n. Получается значение электропроводности каждой соли при её «реальной» концентрации Er. Используя такой подход, учитывается взаимное влияние всех ионов друг на друга.
В результате расчёта измеренное значение электропроводности исходной воды (409 мкСм/см) и рассчитанное значение (408,7 мкСм/см) практически совпали.
В табл. 5 и 6 представлен расчёт электропроводности той же, только полностью умягчённой воды. В качестве катиона в умягчённой воде представлен только натрий. Соответственно, в данной воде существуют только три типа соли и, обратите внимание, отсутствуют соли 2–2.
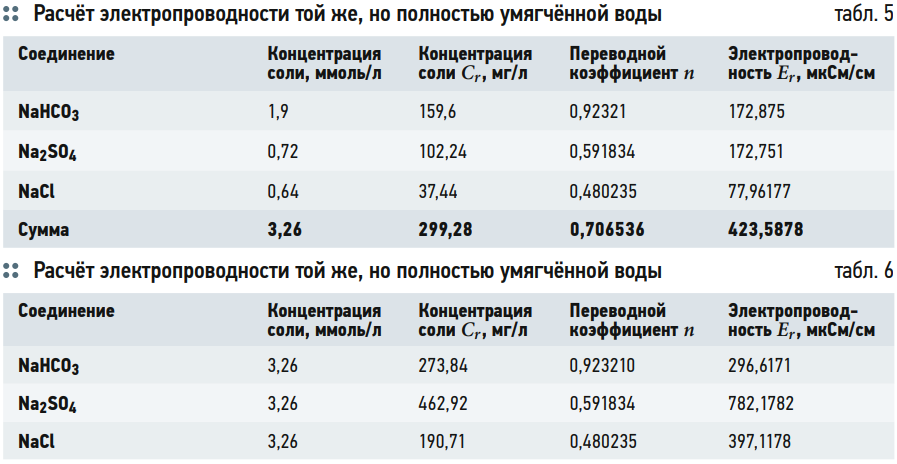
В результате расчёта получаем электропроводность умягчённой воды — 423,58 мкСм/см. Реально измеренная электропроводность умягчённой воды составила 425 мкСм/см. Как видно, в данном случае явно прослеживается то, что умягчённая вода имеет более высокую электропроводность, чем исходная.
Очевидно, что решающее действие на увеличение электропроводности оказывает сульфат. Чем больше сульфата в исходной воде, тем выше электропроводность умягчённой воды по сравнению с исходной.
Было проведено довольно много экспериментов по смешению воды с различной концентрацией ионов, и в целом расчётные значения электропроводностей находились довольно близко к измеренным. В диапазоне до общей концентрации солей до 5 ммоль/л расхождение между измеренными и расчётными значениями было не более 3 мкСм/см. При концентрации более 5 ммоль/л требуется достаточно трудоёмкое определение электропроводностей солей 2–2 в зависимости от концентраций из массива данных. Тем более что при высоких концентрациях начинает сказываться образование ионных пар солей 2–2. Тем не менее, даже при довольно высоких концентрациях до 50 ммоль/л наблюдается неплохая сходимость результатов.
Примеры работы программы расчёта по предлагаемой методике можно посмотреть в [4, 5].
Несколько слов об ионных парах в солях 2–2. Ионные пары в солях сульфата кальция и магния просто отследить, если непрерывно контролировать значение электропроводности умягчённой воды сразу после фильтра умягчения. Дело в том, что в начале фильтроцикла умягчённая вода в качестве катиона содержит только катион натрия. После того, как в умягчённую воду начинает «проскальзывать» кальций или магний, электропроводность воды сразу резко падает. Чем больше «проскок» ионов жёсткости, тем плавней становится линия зависимости электропроводности от жёсткости умягчённой воды, и со временем она приходит к линейному виду, как и предсказывается программой расчёта [6].
Дело в том, что небольшие концентрации кальция и магния связываются сульфатом в ионные пары и перестают переносить электрический заряд. Из-за этого происходит резкое падение электропроводности, поскольку эквивалентное количество натрия, которое было до этого в умягчённой воде, переносило заряд, поскольку натрий не был связан в ионную пару. Так, при концентрации сульфата около 40 мг/л падение электропроводности составило около 3 мкСм/см (при суммарной концентрации кальция и магния 2,8 мг-экв/л). При концентрации сульфата 90 мг/л падение составило около 5 мкСм/см (при суммарной концентрации кальция и магния 3,3 мг-экв/л). То есть в первом случае в ионной паре находилось, если считать по кальцию, 0,011 ммоль/л или 1,5 мг/л CaSO4, во втором случае — 0,018 ммоль/л или 2,45 мг/л CaSO4.
Поэтому при экспериментальном определении эквивалентных электропроводностей соли 2–2 необходимо учитывать наличие погрешности, вызванной ионными парами этой соли.
В солях 2–1, вероятно, если ионные пары и образуются, то в очень маленьких количествах. Так как при «проскальзывании» иона натрия (Н-катионирование после истощения смолы) в воде с сульфатами зависимость электропроводности от концентрации натрия имеет линейный вид. Вероятно, ионными парами в солях 2–1 можно пренебречь, по крайней мере, при концентрациях до 10 ммоль/л.

В заключение
Данной работой на обсуждение выносится прежде всего правомерность использования такого понятия, как принцип равномерного распределения ионов в объёме воды. Этот принцип (если его можно так назвать) не исходит естественным образом из понятия электронейтральности растворов. Использование этого принципа позволяет по крайней мере при малых концентрациях для сильных электролитов различных типов ионов производить довольно точные расчёты значений удельной электропроводности водных растворов, избегая не имеющего физического смысла понятия эквивалентной электропроводности отдельного иона при бесконечном разбавлении. Универсален ли данный принцип или является в этом примере частным случаем?

























