
Введение
Снижение затрат на энергопотребление зданий и сооружений, в частности, экономия электроэнергии на механическую транспортировку воды по стареющим напорным трубопроводам за счёт уменьшения гидравлического сопротивления их внутренних стенок, носит актуальный характер [1, 2]. Это обстоятельство ставит перед проектировщиками определённый круг задач и соответствующих разработок по эффективной и оперативной реконструкции трубопроводного транспорта, в том числе с использованием бестраншейных технологий [3]. Аналогичные задачи ставятся и перед научными работниками и исследователями в виде проведения гидравлических испытаний поступающих на строительные рынки новых альтернативных материалов труб и ремонтных защитных покрытий в целях получения величин их реального гидравлического коэффициента полезного действия. Данные вопросы весьма значимы для менеджеров коммунальных служб, которые должны содействовать обеспечению последующей эффективной эксплуатации трубопроводных сетей [4]. Параллельно с решениями задач обновления ветхого трубопроводного транспорта в отдельных местах размещения трубопроводных систем, например, в зданиях центральных тепловых пунктов, при прокладке труб под землёй, над землёй и т. д., должна решаться комплексная проблема снижения энергопотребления зданий и сооружений [5].

Целью данного исследования является выявление характера изменения величины гидравлического трения от температурных условий транспортируемой воды и окружающей среды в определённых диапазонах с последующей возможностью управления процессом транспортировки посредством достижения минимума затрат на электроэнергию.
Обеспечение поставленной задачи осуществляется за счёт проведения экспериментальных гидравлических исследований на крупногабаритных стендах, а также с использованием расчётно-аналитического подхода (с использованием вычислительных комплексов) по определению динамики изменения гидравлических показателей трубопроводов [6]. Также при этом производится моделирование параметров в широком спектре варьирования температуры транспортируемой жидкости и окружающей среды.
Теоретическая и практическая значимость работы состоит в определении оптимального температурного режима (диапазона), который позволяет снизить потребление электроэнергии на транспортировку воды по напорным трубопроводам. Наиболее известными и значимыми публикациями по данной тематике являются [7, 8], в которых отражён комплекс вопросов экономии электроэнергии в системах транспорта питьевой и технической воды.
Нерешёнными проблемами является необходимость и возможность совершенствования управления трубопроводными сетями в плане обеспечения экономии электрической энергии при транспортировке воды в различных температурных условиях.
В области гидравлики трубопроводных систем используется значительное число методик определения коэффициента гидравлического трения [9, 10]. В тех случаях, когда затрагивается фактор влияния температуры транспортируемой по трубопроводу жидкости на величину коэффициента гидравлического трения, методические подходы требует дополнительной интерпретации [11]. Как известно, базовым условием определения коэффициента гидравлического трения для любого материала трубопровода является проведение стендовых экспериментальных исследований. При этом возможно моделирование тепловых режимов с поиском новых зависимостей для определения коэффициента гидравлического трения при условии соблюдения ограничительных диапазонов по ряду параметров.
На практике возможен симбиоз опытного и аналитического подходов к определению динамики и диапазонов изменения отдельных гидравлических характеристик потока и, в частности, величины коэффициента гидравлического трения при разных температурных условиях прокладки и эксплуатации трубопроводов. Аналитические методы сопровождаются моделированием, которое позволяет оперативно сопоставлять опытные и расчётные значения коэффициентов гидравлического трения с анализом величин их возможных расхождений в строгих рамках установленных оптимальных диапазонах значений чисел Рейнольдса и динамических вязкостей.

Материалы и методы исследований
Исследования включали выполнение гидравлических экспериментов и расчётно-аналитических операций и обоснований, где объектом изучения являлись напорные трубы из непластифицированного поливинилхлорида (НПВХ), а именно:
- экспериментальных гидравлических испытаний, реализуемых в Лаборатории кафедры «Водоснабжение и водоотведение» НИУ МГСУ (первый этап исследований);
- автоматизированной обработки полученных данных на предмет выявления динамики изменения коэффициента гидравлического трения L при различных температурах стенки трубы и транспортируемой воды (второй этап исследований);
- автоматизированного поиска оптимальных параметров управления процессом транспортировки воды на базе выявления минимальных значений потребления электроэнергии Э в соответствующих температурных условиях (третий этап исследований).
Для обработки результатов гидравлических экспериментов и проведения расчётно-аналитических операций и последующего анализа использовались специальное программное обеспечение. Таким образом, рассматриваемыми в статье методами являются: экспериментальные исследования и моделирование ситуаций при изменении температурных режимов с использованием теории полуэмпирической турбулентности.

Фото 1. Гидравлический стенд с трубопроводами из различных материалов
Первый этап исследований осуществлялся на крупногабаритном стенде, общий вид которого представлен на фото 1. Экспериментальные исследования проводились при температуре воды и окружающего пространства 16°C.
Результатами эксперимента являлось определение значений коэффициентов гидравлического трения Lо для трубы из НПВХ внутренним диаметром 0,1046 м в широких диапазонах расходов.
Второй этап исследований заключался в моделировании работы трубопровода в целях выявления динамики изменения коэффициента гидравлического трения L в зависимости от температурного условий, в частности, температуры стенки трубопровода при стабильной температуре транспортируемой воды. Исследуемыми величинами являлась такая физическая характеристика, как динамическая вязкость, которая зависит от рода жидкости и температуры, а также кинематическая вязкость, представляющая собой отношение динамической вязкости к плотности жидкости.
По результатам автоматизированного расчёта отслеживались и подвергались анализу промежуточные значения таких показателей, как числа Рейнольдса, соотношения динамических вязкостей, а также соотношения расчётного и опытного значений коэффициентов гидравлического трения для труб.
В алгоритме автоматизированных программ представлены формулы:
- расчётного коэффициента гидравлического трения:
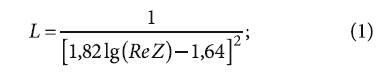
- числа Рейнольдса:

(величина Re находится в диапазоне от 2,8×104 до 4,5×105);
- величины коэффициента динамической вязкости, отнесённого к потоку жидкости:
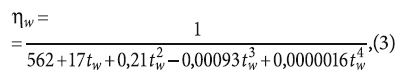
где tw — температура транспортируемой воды;
- величины коэффициента динамической вязкости, отнесённого к температуре стенки трубы:
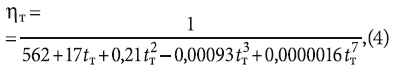
где tт — температура стенки трубопровода;
- величины коэффициента кинематической вязкости жидкости:
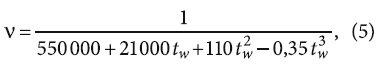
- величины соотношения динамических вязкостей:

(значение Z находится в диапазоне от 2,5 до 0,83);
- соотношения расчётного L и опытного Lo значений коэффициентов гидравлического трения:
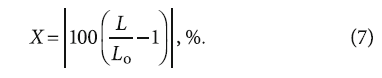
Третий этап исследований заключался в автоматизированном поиске оптимальных параметров управления процессом транспортировки воды на базе выявления минимальных значений потребления электроэнергии Э. Для этого в алгоритме программы заложен следующий математический аппарат.
Потребление электроэнергии Э [ кВт·ч] на преодоление потерь напора при транспортировке воды по напорным трубопроводам рассчитывается по следующей базовой формуле:
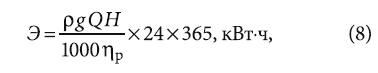
где ρ — плотность жидкости, кг/м³; g — ускорение свободного падения, м/с2; Q — расход подаваемой трубопроводом воды, м³/с; ηp — коэффициент полезного действия насосной установки; 24 — количество часов работы насоса в сутки, ч; 365 — количество дней в году; 1000 — коэффициент перевода из [Вт] в [ кВт]; Н — потери напора в трубопроводе определённой длины, м вод. ст.
Выражая потери напора Н через удельное сопротивление трубопровода соответствующего материала изготовления Аi [с2/м6], длину l [м] и расход Q [ м³/с], получаем формулу:
H = AilQ2. (9)
В рассматриваемом случае транспортировки воды, то есть при ρ = 1000 кг/м³, g = 9,81 м/с2, а также при проведении математических операций преобразования, базовая формула (8) запишется в виде:
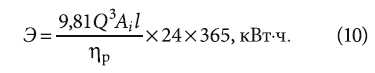
В том случае, если удельное сопротивление трубопровода А неизвестно, то возможно использование величины коэффициента гидравлического трения L для трубопровода соответствующего материала и диаметра d [м].
Из формулы Дарси — Вейсбаха (11) следует, что:
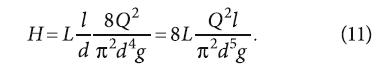
При транспортировке воды, то есть при значениях ρ = 1000 кг/м³, g = 9,81 м/с2, а также по результатам проведении математических операций преобразования Н базовая расчётная формула для определения затрат электроэнергии запишется:
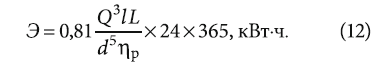
Таким образом, для расчёта потребления электроэнергии при транспортировке воды по напорным трубопроводам могут использоваться равнозначные формулы (10) или (12), которые были заложены в алгоритм расчётной программы.
Результаты исследований
Результатами первого этапа исследований явилось определение массива опытных значений коэффициента гидравлического трения Lо для соответствующих величин расхода транспортируемой воды. Например, при расходе воды Q = 0,0043 м³/с величина Lо составила 0,02305 (табл. 1).
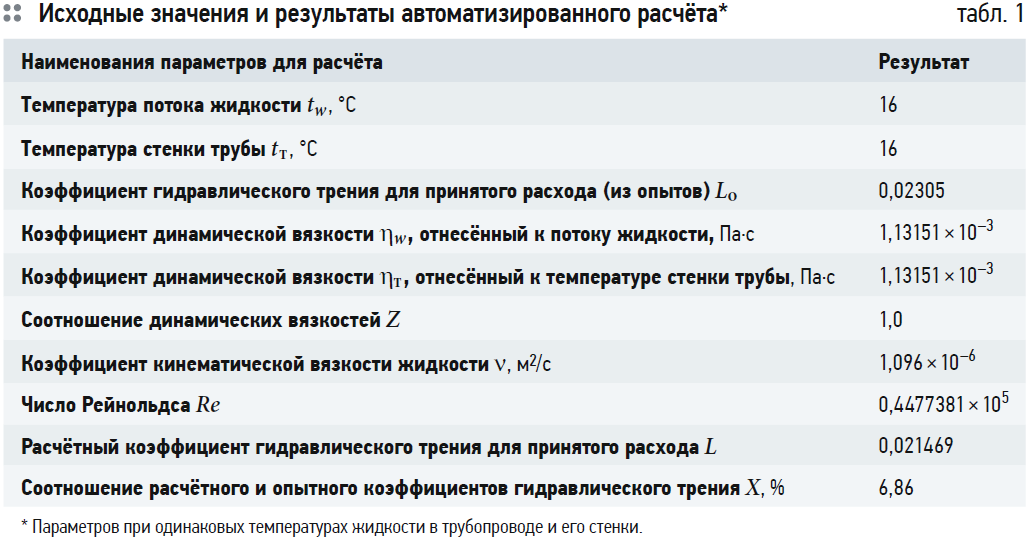
Результатами второго этапа исследований явилось получение и анализ соотношения опытного Lо и расчётного коэффициентов гидравлического трения L в зависимости от температурных условий, в частности, температуры стенки трубопровода при стабильной температуре транспортируемой воды. В табл. 1 в упрощённом виде представлена входная и выходная информация по результатам автоматизированного расчёта при произвольно выбранном расходе воды (Q = 0,0043 м³/с) и одинаковых температурах воды и стенки трубы.
Анализ данных табл. 1 свидетельствует о следующем: при одинаковых температурах жидкости и наружной стенки трубы (16°C), а также в оптимальных диапазонах чисел Рейнольдса Re и установленного соотношения динамических вязкостей Z расчётные коэффициенты гидравлического трения L отличаются от экспериментального значения Lо на X = 6,86%. Для инженерных систем эта величина является допустимой и позволяет использовать формулу (1) для приближённых расчётов коэффициента гидравлического трения, не прибегая к экспериментальным исследованиям на гидравлических стендах в иных условиях.
Также в задачи второго этапа исследований входил анализ динамики изменения значений коэффициента гидравлического трения L от температуры стенки трубы tт. Расчёты проводились при трёх величинах расходов: 0,00322 (№1), 0,00694 (№2) и 0,01303 (№3) м³/с. Для каждого из режимов величина температура воды в трубопроводе принималась постоянной и равной 16°C.
Пошаговому изменению подлежала лишь температура стенки трубы от 9,5 до 61,5°C, что соответствовало жёстким рамкам сохранения рекомендуемых параметров для Z, то есть в диапазоне от 0,839 до 2,498, и чисел Рейнольдса Re в установленном интервале {2,8×104; 4,5×105}.
По результатам автоматизированного расчёта отслеживалась динамика изменения величины L, что иллюстрируется графическими зависимостями на рис. 1.
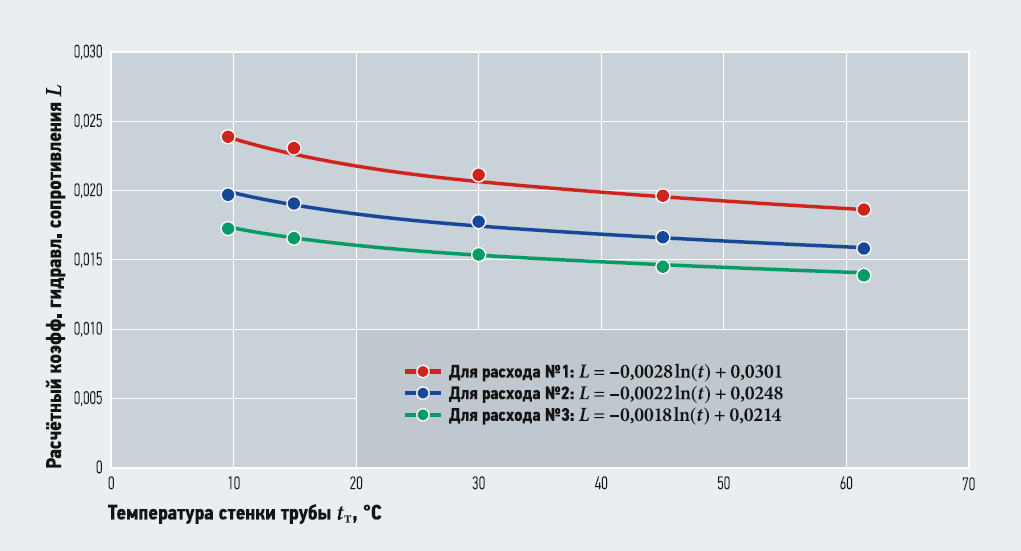
Рис. 1. Зависимость величины коэффициента гидравлического трения от динамической вязкости, отнесённой к температуре стенки трубы
Представленные на рис. 1 кривые свидетельствуют об идентичном характере изменения коэффициента гидравлического трения от температуры для соответствующих значений расхода воды. С повышением температуры стенки трубопровода коэффициент гидравлического трения снижается при всех режимах расхода воды примерно на 20,6–23,5%, что можно охарактеризовать как положительный эффект: при обогреве трубопровода гидравлические сопротивления движению жидкости уменьшаются. Данное обнаруженное обстоятельство явилось предметом третьего этапа исследований, состоявшего в выявлении содействия экономии электроэнергии при транспортировке воды по напорным водопроводным сетям с относительно высокой температурой наружных стенок. Иначе при размещении трубопровода в зоне низких температур (например, зимой под землёй) его холодная наружная поверхность будет провоцировать повышение гидросопротивлений, оказывая влияние непосредственно на динамическую вязкость пограничного слоя. Такая задача становится актуальной для условий вечной мерзлоты, например, при подземной или наземной прокладках трубопроводов, когда необходима экономия затрат электроэнергии при транспортировке воды.
Результатом третьего этапа исследований являлся поиск областей температур стенки трубопровода и транспортируемой воды, при которых обеспечивается минимальное потребление электроэнергии. Тем самым выявляется диапазон оптимального управления параметрами работы трубопроводной системы.
Для реализации поставленной задачи на базе полученных математических зависимостей, наглядно представленных на рис. 1, был осуществлён поисковый расчёт динамики изменения коэффициента L для трёх указанных выше значений расходов воды при выборочном массиве значений температур стенки трубы — 9,5, 15, 30, 45 и 61,5°C, когда соблюдаются условия сохранения величин параметра Z и чисел Рейнольдса Re в установленных интервалах.
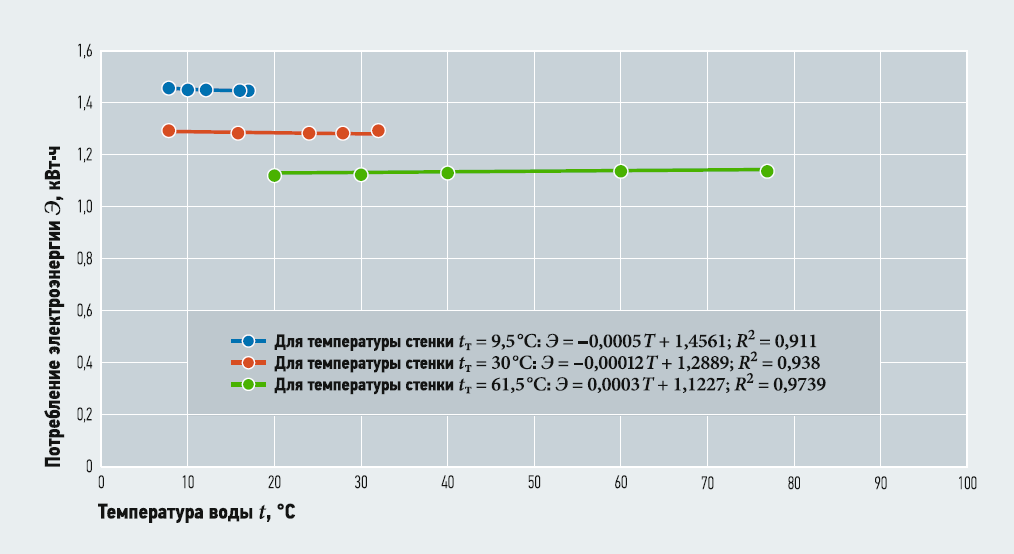
Рис. 2. Потребление электроэнергии и диапазоны температур воды и стенок трубопровода при расходе транспортируемой воды Q = 0,00322 м3/с и температуре воды 16 °C
На основе данных, полученных по результатам работы автоматизированного комплекса, на рис. 2–4 представлены выборочные кривые потребления электроэнергии, описываемые линейными зависимостями. Таким образом, диапазон, ограниченный начальными и конечными значениями температур воды на трёх кривых, а также их взаимное расположение иллюстрируют собой возможные затраты электроэнергии на транспортировку воды при её различных температурах и расходах с выборочными стабильными температурами стенок трубопроводов — 9,5, 30, 45 и 61,5°C.
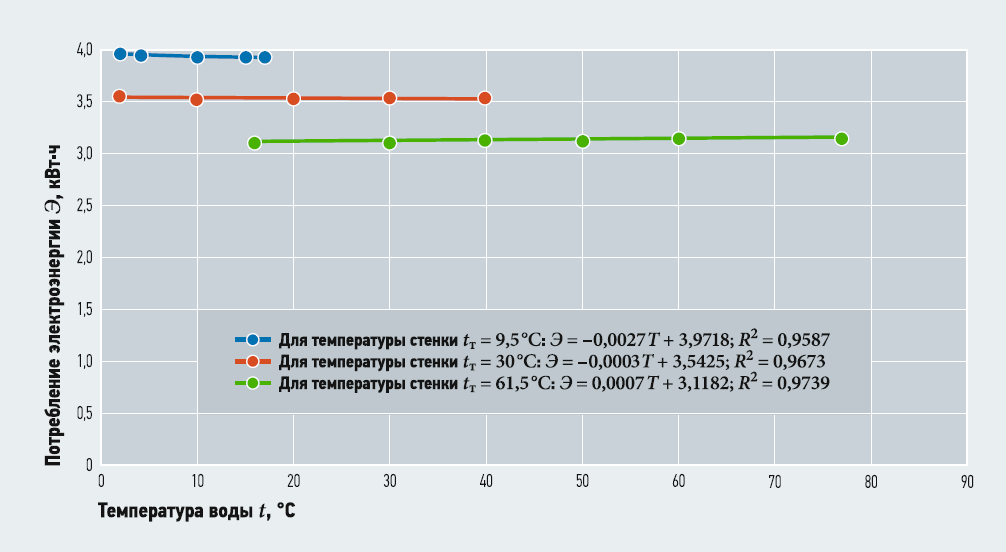
Рис. 3. Потребление электроэнергии и диапазоны температур воды и стенок трубопровода при расходе транспортируемой воды Q = 0,00694 м3/с и температуре воды 16 °C
Обобщая данные, представленные на рис. 2–4, можно сделать ряд базовых выводов в отношении расходов воды и потребления электроэнергии при неизменном диаметре трубы:
- чем выше расход транспортируемой воды и чем ниже температура стенки трубопровода, тем больше энергозатраты на транспортировку воды (например, для рис. 2 значение Э при температуре стенки трубы 9,5°C составляет 1,45 кВт·ч, а для рис. 4 — порядка 22,45 кВт·ч);
- чем выше температура транспортируемой воды, тем меньше потребляется электроэнергии и наблюдается больший расчётный диапазон потенциального эффективного управления работой трубопроводной системы, что можно оценить разной протяжённостью кривых потребления электроэнергии (например, для рис. 2–4 наибольшая протяжённость кривых потребления электроэнергии наблюдается при температурах стенки трубы 61,5°C в диапазоне изменения температуры воды приблизительно 15–78°C).
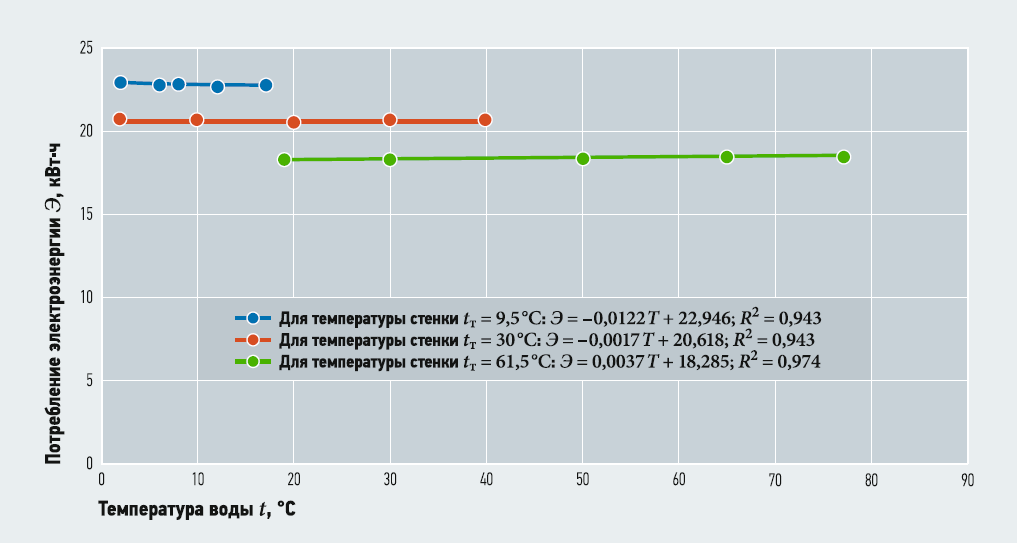
Рис. 4. Потребление электроэнергии и диапазоны температур воды и стенок трубопровода при расходе транспортируемой воды Q = 0,01303 м3/с и температуре воды 16 °C
Подводя итоги анализа графического материала, можно отметить, что в перспективе менеджеры коммунального хозяйства, обладая данными автоматизированного расчёта или полученными на их базе оптимальными областями работы системы трубопроводов, могут обеспечить для соответствующего варианта эксплуатации трубопроводных систем минимальные значениями потребления электроэнергии, в том числе при различных значениях коэффициента полезного действия насосных установок.
Ниже представлен комплексный анализ полученных результатов автоматизированного расчёта потребления электроэнергии для трёх вариантов указанных выше расходов в плане возможности управления процессом транспортировки воды при разных температурах стенки трубопровода и транспортируемой воды для обеспечения минимального потребления электроэнергии.
Для универсальности подхода в каждом из рассматриваемых вариантов принималось значение потребления электроэнергии Э в кВт·ч на 1 п.м. трубопровода в год. При этом для сравнения анализу подлежало значение коэффициента полезного действия 0,95 (как у современных высокоэффективных насосов).
Расчётные данные позволяют выявить определённые тенденции для двух случаев: при стабильной температуре воды 16°C (первый случай) и стабильной температуре стенки трубопровода 16°C (второй случай).
Суть полученных результатов для первого случая может быть интерпретирована следующим образом:
1. При относительно большом расходе Q = 0,01303 м³/с, стабильной температуре транспортируемой жидкости tж = 16°C, а также росте температуры стенки трубопровода в интервале 12–25°C наблюдается снижение потребления электроэнергии в диапазоне от 22,442 до 20,993 кВт·ч, соответственно, то есть на 6,5%. При повышении температуры стенки трубы тенденция сохраняется вплоть до 61,5°C — при данной температуре потребление электроэнергии снижается до 18,368 кВт·ч, то есть общее снижение составляет 18,15%.
2. При среднем расходе Q = 0,00694 м³/с и тех же температурных условиях наблюдается снижение потребления электрической энергии в диапазоне от 3,878 до 3,617 кВт·ч, соответственно, то есть на 6,7%. При этом абсолютные значения потребления электроэнергии стабильно снижаются при росте температуры стенки трубы в указанном диапазоне в 21,957/3,789 = 5,8 раза. При повышении температуры стенки трубы до 61,5°C при прочих равных условиях наблюдается сохранение тенденции снижения значения потребления электроэнергии до 3,132 кВт·ч, то есть на 19,24% от начальной в рассматриваемом диапазоне (от 12 до 61,5°C).
3. При относительно малом расходе Q = 0,00322 м³/с и тех же температурных условиях картина повторяется подобно случаям 1 и 2, но с несколько меньшими абсолютными значениями потребления электроэнергии. В частности, в диапазоне температуры стенки трубы 12–61,5°C снижение потребления электроэнергии составляет от 0,462 до 0,367 кВт·ч, соответственно, то есть на 20,5%.
Анализируя возможности управления процессом обеспечения экономии электроэнергии при транспортировке воды со стабильной температурой 16°C в диапазоне указанных расходов (от 0,01303 до 0,00322 м³/с), можно сделать следующие выводы. Процесс управления работой трубопроводной системы в плане достижения ожидаемой величины потребления электроэнергии возможен в относительно широких диапазонах температуры стенки трубопровода (12–61,5°C), причём подобная тенденция сохраняется и при увеличении температуры транспортируемой воды до 25°C. При этом границы диапазона температуры стенки трубы изменяются от 16 до 75°C, соответственно, что расширяет возможности расчётного метода для отслеживания потребления электроэнергии. Выход за установленные пределы не гарантирует правильность результатов расчёта потребления электроэнергии и возможности управления работой системы трубопроводов.
Полученные результаты для случая №2 могут быть интерпретированы так:
1. При относительно большом расходе Q = 0,01303 м³/с, стабильной температуре стенки трубы tт = 16°C для интервала температур транспортируемой воды от 12 до 25°C наблюдается сравнительно постоянное потребление электроэнергии в диапазоне от 21,974 до 21,964 кВт·ч, соответственно, то есть разница составляет порядка 0,05%. Увеличение температуры транспортируемой воды свыше 25°C не позволяет произвести оценку потребления электроэнергии расчётно-аналитическим путём, так как расчётные величины гидравлических показателей выходят за рамки установленных значений.
2. При среднем расходе Q = 0,00694 м³/с, стабильной температуре стенки трубы tт = 16°C для интервала температур транспортируемой воды 12–25°C наблюдается практически постоянное энергопотребление на уровне 3,78–3,79 кВт·ч. Какое-либо повышение температуры транспортируемой воды не позволяет произвести корректные расчёты, так как гидравлические показатели выходят за рамки установленных значений.
3. При малом расходе Q = 0,00322 м³/с, стабильной температуре стенки трубы (16°C) для интервала температур транспортируемой воды 12–25°C наблюдается практически постоянное энергопотребление на уровне 0,451 кВт·ч. Как и в случаях 1 и 2, какое-либо повышение температуры транспортируемой воды не позволяет произвести расчёты, так как гидравлические показатели выходят за рамки установленных значений.
Анализируя возможности управления процессом обеспечения экономии электроэнергии при стабильной температуре стенки трубы 16°C в диапазоне указанных расходов (0,01303–0,00322 м³/с), можно сделать выводы: управление работой трубопроводной системой в плане ожидаемой величины потребления электроэнергии возможно в диапазоне температур транспортируемой воды 12–25°C. При повышении температуры воды расчётные показатели гидравлических характеристик выходят за рамки установленных значений. В то же время при изменении температуры стенки трубы до 25°C возможности расчёта потребления электроэнергии и управления процессом эффективной транспортировки воды возрастают, так как верхняя граница расчётного диапазона температур транспортируемой воды для всего диапазона рассматриваемых расходов может быть увеличена до 35°C при сохранении нижней границы диапазона 12°C.
Выводы
1. Проведён комплексный анализ работы трубопровода НПВХ определённого диаметра на предмет определения его гидравлических характеристик и потребления электроэнергии в широких диапазонах температур стенки трубы и воды.
2. Установлено, что аналитическое отслеживание потребления электроэнергии системой трубопроводов возможно в определённых диапазонах температур стенки труб и транспортируемой воды.
3. Произведена оценка возможности управления процессом обеспечения экономии электроэнергии при транспортировке воды при различных температурах путём использования автоматизированных комплексов и разработанных исходя из результатов расчёта рекомендаций.
4. Определены температурные границы, позволяющие менеджерам коммунальных служб эффективно управлять процессом транспортировки воды с минимальными затратами электроэнергии.
5. Представленный материал является базой для проведения аналогичных экспериментальных и расчётно-аналитических исследований для трубопроводов из других, альтернативных материалов в целях определения наиболее экономичного варианта проектирования и эксплуатации напорных трубопроводов в широком диапазоне расходов воды и диаметров труб.
























