Статья ВАК: Практическое применение явления аномально высокой амплитуды автоколебательного процесса при истечении жидкости. Часть 1

Введение

Автоколебательные течения из отверстий, перекрытых арочным элементом, представляют большой практический и исследовательский интерес в научно-инженерных задачах распределения воздуха, диспергирования жидкостей, смешения плохо смешивающихся жидкостей, сжигания топлив. Однако работ по изучению механизма возникновения течения и характеристик автоколебательного процесса крайне мало.

Сегодня уже понятно, что обнаруженное аномально быстрое затухание результирующего потока вентиляционного воздуха в окружающей среде, отмеченное в [1], имеет в своей природе мощный автоколебательный процесс.

Это первое в литературе упоминание трактовалось как эффект соударения оппозитно-встречных струй в приложении к технике вентиляции.

Взаимодействию двух встречно-соосных потоков посвящены работы [2, 3].

В работе [2] представлены результаты экспериментальных исследований течений воздуха из лункообразных отверстий. Установлено быстрое падение скорости потока вниз по течению от лункообразного отверстия. При объяснении механизма гашения скорости потока при истечении из отверстия не был отмечен факт наличия колебательного процесса.

В работе [3] представлены первые попытки исследования процесса методами численного моделирования. Результаты расчётов показали наличие периодического автоколебательного течения. Проведена оценка влияния геометрических параметров отверстия на характеристики автоколебательного процесса.

Установлено, что спектр и амплитуда колебаний потока зависят от длины прямоугольного отверстия, отнесённой к его ширине.

Первая попытка комплексного подхода к изучению механизма возникновения автоколебательного течения из отверстия, перекрытого арочным элементом, с применением методов численного моделирования представлена в работе [4]. Рассмотрены отверстия с различными геометрическими параметрами и при различных кинематических режимах течения.

Для диапазона чисел Рейнольдса (Re) 2,1×10⁶–1,2×10⁷ установлено, что автоколебательный характер течения не зависит от кинематических параметров течения, в частности, Sh ≠ f(Re). Однако установлена существенная зависимость амплитуды колебательного течения от величины отношения l/d.

При l/d = 1 автоколебательный характер течения выражен слабее и имеет сниженную амплитуду колебаний. При l/d = 2 наблюдается ярко выраженное автоколебательное течение. При l/d = 4 также наблюдается автоколебательный характер течения, но, в отличие от предыдущих вариантов, этот процесс протекает менее периодично, появляются дополнительные гармоники колебаний, а амплитуда колебаний значительно снижается. 

Определяя относительную амплитуду колебаний как отношение амплитуды колебаний модуля скорости потока к среднерасходной скорости, специалисты установили, что относительная амплитуда автоколебаний для иных видов автоколебательных течений, как правило, не превышает значения 0,9. Например, в работах [5–6], в которых исследуется истечение плоской струи в прямоугольную полость, относительная амплитуда автоколебаний не превышает значения 0,4. В работах [7–9], в которых исследуется автоколебательный процесс при обтекании тел различной формы, относительная амплитуда колебаний также не превышает значения 0,9, а в работах [10–11], в которых исследуется автоколебательный процесс фонтанирования вертикальной плоской струи жидкости, относительная амплитуда колебаний не превышает значения 0,6.

В работах [12–13], в которых исследуется обтекание внешним потоком прямоугольных каверн при Re = 10³–10⁵, амплитуда автоколебаний не превышает значения 0,9.

В настоящей работе численно исследуется автоколебательный режим истечения из отверстия перекрытого арочным элементом. Главной целью исследования является выяснение механизма формирования автоколебательного течения, а также определение основных его характеристик. Рассматривается вариант геометрии отверстия с соотношением сторон l/d = 2, поскольку при данном соотношении наиболее ярко наблюдается автоколебательный режим истечения [4]. По результатам моделирования определяется распределение поля амплитуд колебаний в плоскости течения струи.

Постановка и метод решения задачи

Исследуется автоколебательное течение вязкого изотермического несжимаемого газа из прямоугольного отверстия, перекрытого арочным элементом (рис. 1).

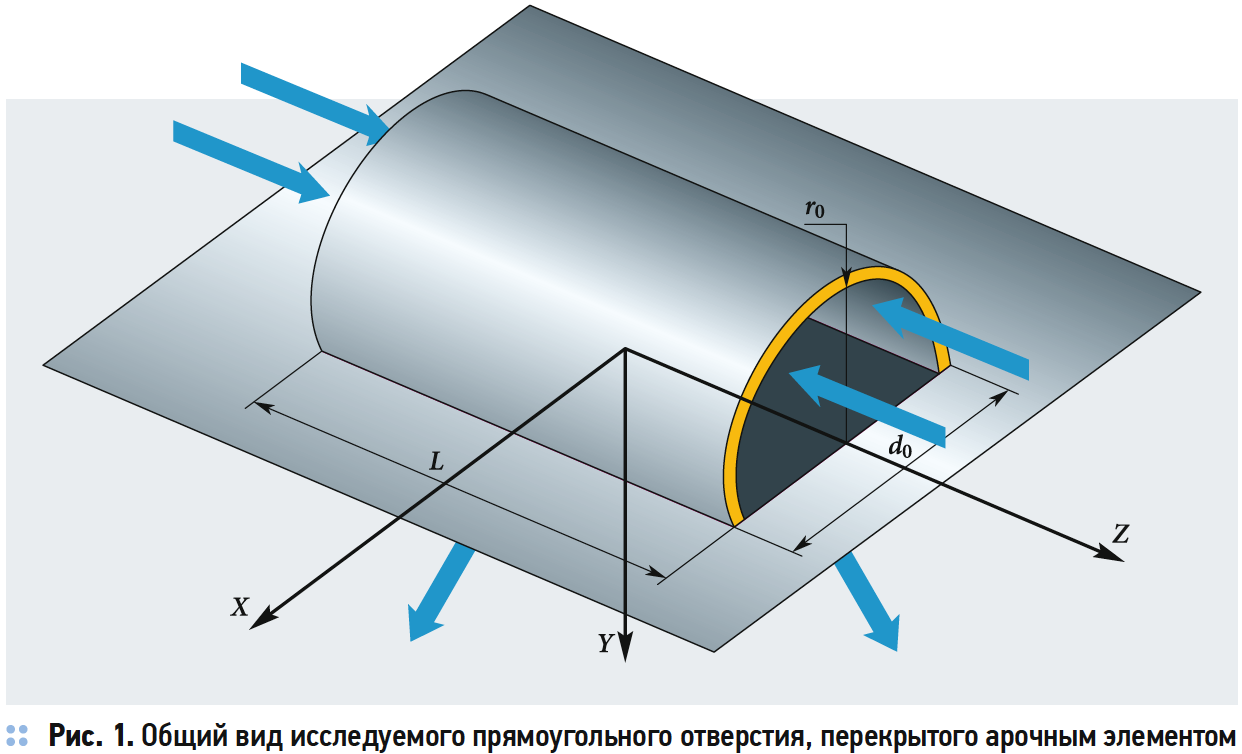
Для описания трёхмерного турбулентного течения жидкости использовался метод крупных вихрей (Large Eddy Simulation, LES) [14], базирующейся на решении отфильтрованных по пространству уравнений Навье-Стокса и уравнения неразрывности (1.1–1.2):

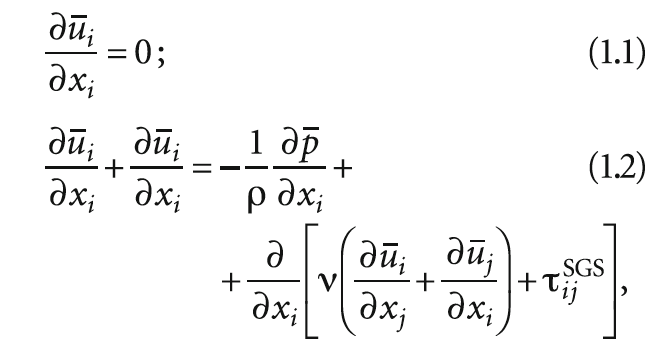
здесь ν — коэффициент кинематической вязкости; u_i и p — отфильтрованные по пространству компоненты скорости и давление, соответственно.

Крупномасштабные вихри разрешаются напрямую из уравнений (1.1–1.2), а мелкомасштабные вихревые структуры моделируются в соответствии с моделью подсеточной вязкости (SubGrid-Scale, SGS) Смагоринского.

В соответствии с моделью Смагоринского делаются два допущения. Во-первых, предполагается линейная связь между тензором подсеточных напряжений и тензором скоростей деформации:

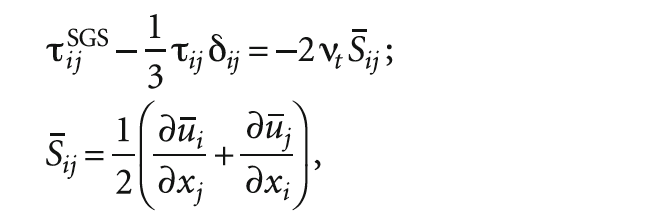
где S_ij — тензор скоростей деформации, построенный по осреднённым значениям скорости; ν_t — подсеточная вихревая вязкость. Во-вторых, по аналогии с моделью длины смешения [14] для расчёта подсеточной вязкости:

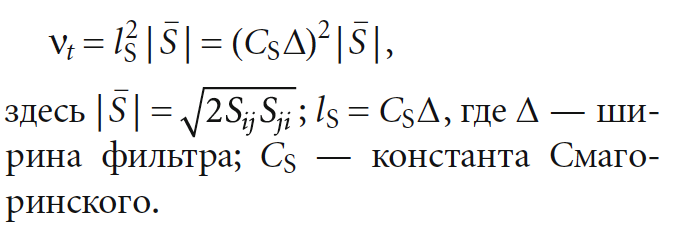
На рис. 2 показана схема отверстия, площадь входного сечения которого равна 0,15 м², а скорость во входном сечении в расчётную область составляет 0,039 м/с. Скорость во входном сечении определяется из условия, что скорость потока из отверстий арочного элемента составляет v₀ = 3 м/с, а площадь прямоугольного отверстия равна 0,005 м². На выходной границе расчётной области распределение давления p = const и условие Неймана на тангенциальные компоненты скорости ∂uτ/∂n→ = 0. Все остальные границы расчётной области предполагаются твёрдыми стенками и на них ставятся условия прилипания.

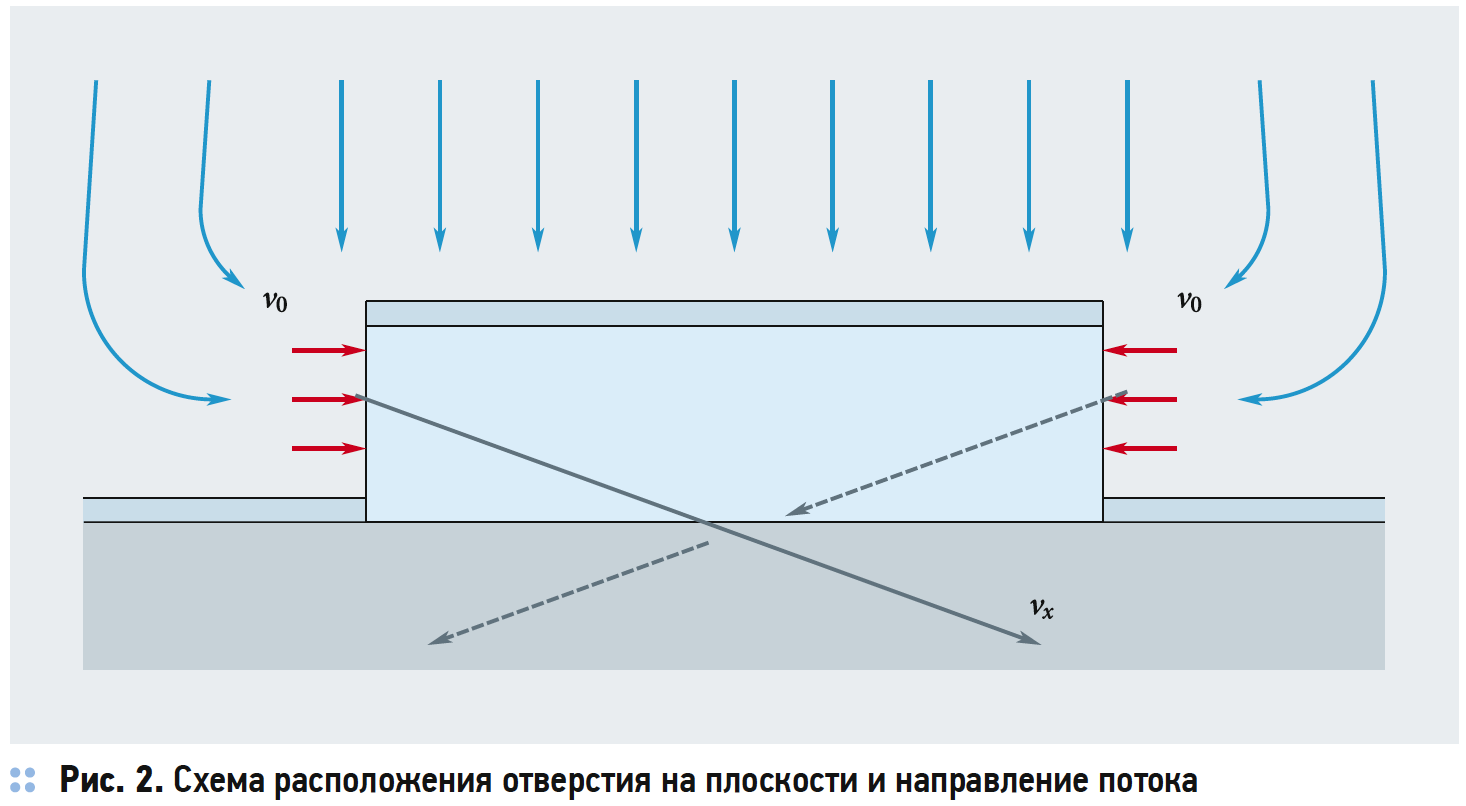
Для решения поставленной задачи использовался вычислительный программный комплекс STAR-CCM+ (ver. 8). Пространственная аппроксимация уравнений переноса (1.1–1.2) выполняется с помощью метода контрольных объёмов. Для интегрирования по времени используется неявная схема первого порядка точности.

Аппроксимация конвективных членов в уравнении переноса импульса (1.1) выполняется по схеме центральных разностей второго порядка точности. Решение систем алгебраических уравнений, формируемых при дискретизации уравнений переноса, производится алгебраическим многосеточным методом [15].

В исследуемой области построена гексаэдральная неструктурированная расчётная сетка с более подробным разрешением в области отверстия. Размер элемента расчётной сетки в области максимального сгущения составляет 0,3 мм, а максимальный размер элемента расчётной сетки составляет 80 мм.

Общее количество ячеек расчётной сетки составило 22×106.

Механизм возникновения автоколебаний

Для понимания особенностей механизма возникновения автоколебаний при истечении жидкости из рассматриваемого отверстия необходимо точно воспроизвести картину течений и взаимодействий потоков между собой. Использование подхода LES позволяет получить подробную картину течения, напрямую разрешая наиболее крупные вихревые структуры потока, соответствующие длинноволновой части инерционного интервала энергетического спектра. На рис. 3–4 представлено развитие течения потока из отверстия за время одного полупериода его колебаний. Данное явление представляет собой динамически неустойчивое периодическое течение, вызванное сложным неустойчивым взаимодействием встречно-соосных потоков, истекающих через отверстие.

Характеристики автоколебаний

Интерес к данному виду автоколебательных течений вызван аномально высокой относительной амплитудой колебаний потока, которая, как следует из рис. 3а, принимает значения от 5,0 до 6,0.

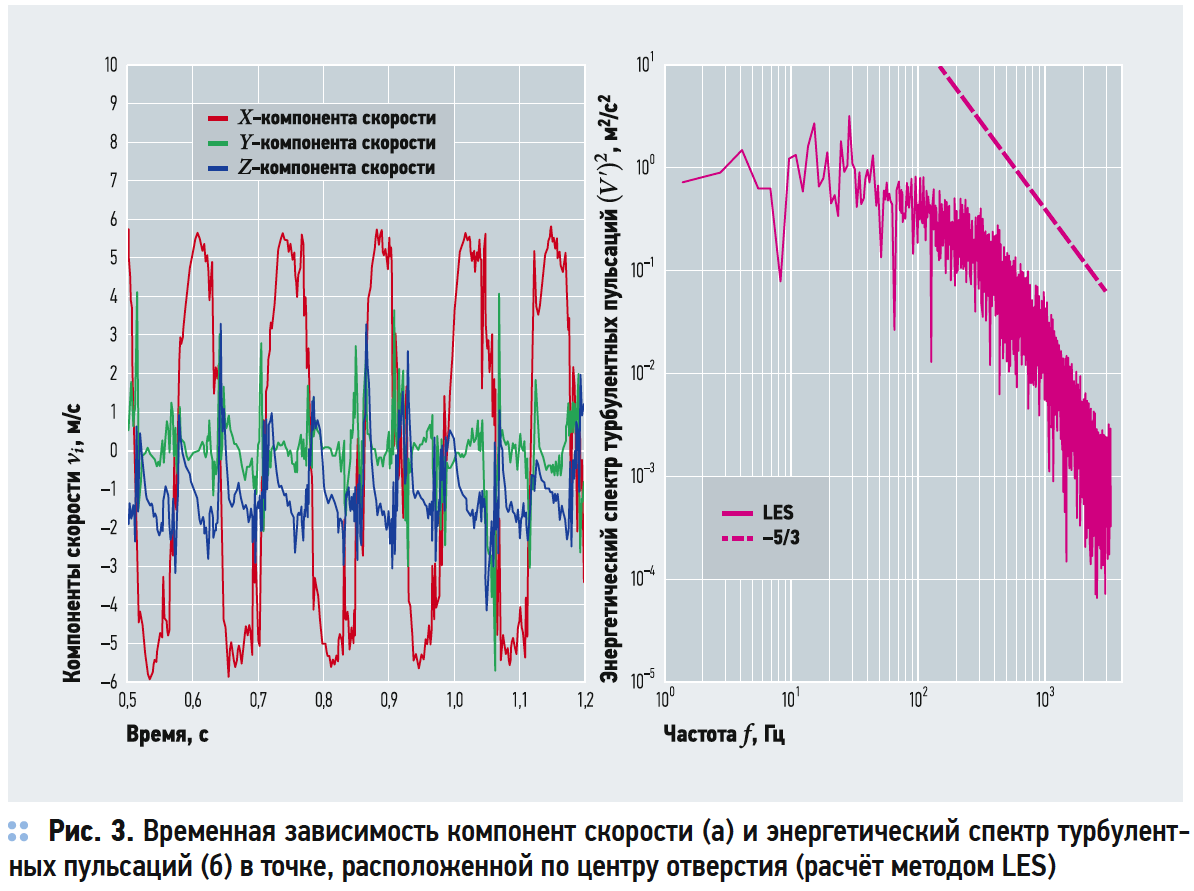
Для определения энергетического спектра турбулентных пульсаций потока (рис. 3б) и амплитуды колебаний по перпендикулярной и продольной осям отверстия (Y и X на рис. 2, соответственно) определяется временная зависимость всех компонент скорости (рис. 3а).

В результате анализа полученных данных определяется распределение амплитуды автоколебаний (рис. 4).

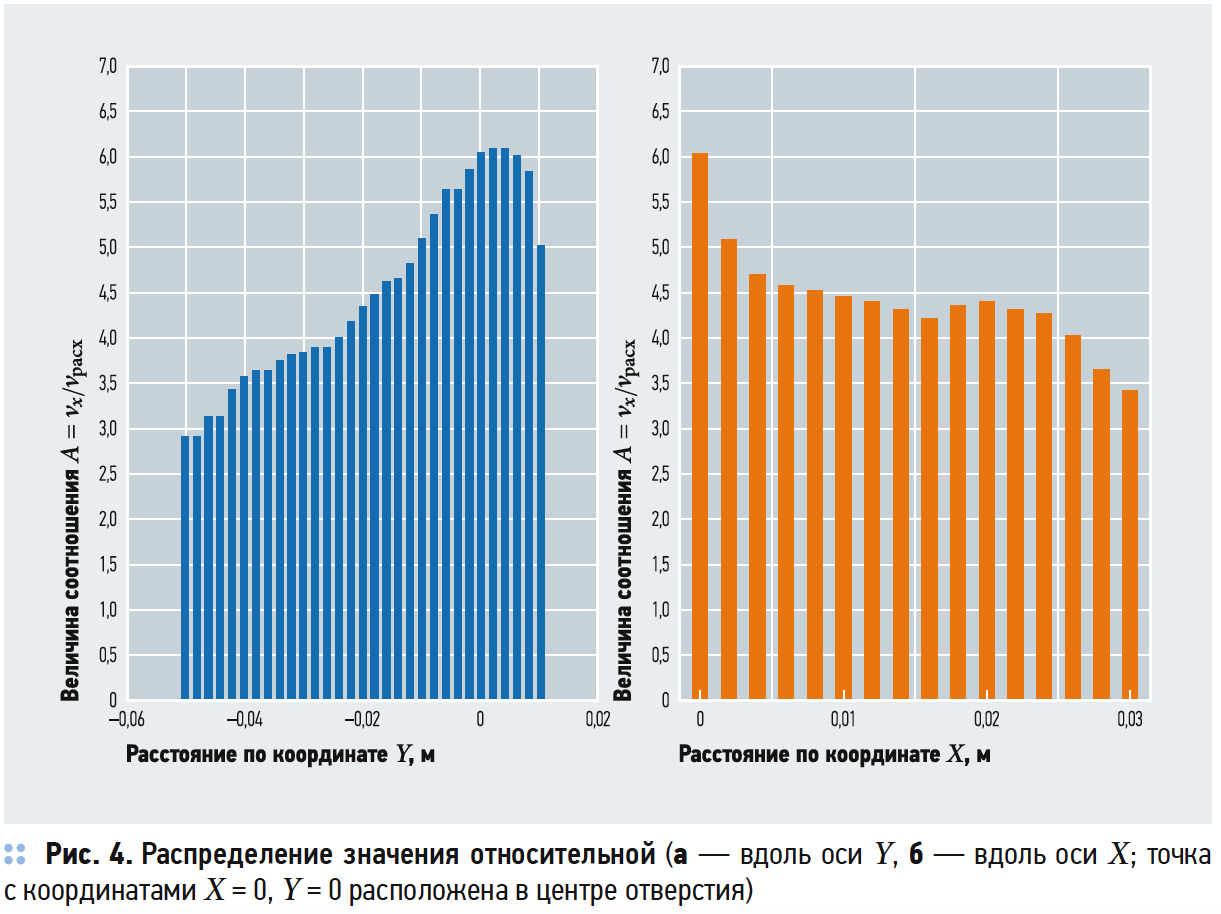
Значение амплитуды колебаний соответствует отношению максимальной поперечной компоненты скорости vx к среднерасходной скорости из отверстия при заданных условиях: A = vx /vрасх.

Установлено, что максимальное значение амплитуды колебаний достигается по центру отверстия на расстоянии от 0 до 4 мм от плоскости отверстия (по оси Y, рис. 4а). Принимая во внимание, что площадь прямоугольного отверстия формируется как d₀L = 0,05×0,1 м², можно полагать, что максимальные колебания обнаруживаются в плоскости данного конкретного отверстия.

Вывод

Численно исследован автоколебательный процесс при истечении из прямоугольного отверстия с соотношением сторон 2:1, перекрытого арочным элементом. В рассмотренном варианте фигурирует отверстие с соотношением l/d₀ = 2.

Также дано объяснение механизму возникновения автоколебательного характера течения.

Сложное взаимодействие двух встречно-соосных потоков обеспечивает периодический подпор одного из них, как следствие организуя устойчивый колебательный характер течения.

При этом оказывается, что точки максимальных значений амплитуды колебательного процесса лежат практически в плоскости отверстия, отступая от неё на расстояние 2–4 мм.

Относительная амплитуда автоколебаний рассматриваемого течения аномально высока и принимает значения 5,0–6,0, в то время как в иных известных автоколебательных течениях она составляет 0,4–0,9. Видно, что соразмерный рост амплитуды составляет 5,0–15,5 раз.

Описанному выше явлению мы дали название АВААК.

АВААК — это явление аномально высокой амплитуды автоколебательного процесса при истечении ньютоновской жидкости из прямоугольного отверстия, перекрытого арочным элементом.