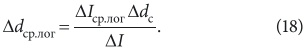
Рис. 1. Изменение перепадов теплосодержаний и температур в оросительных камерах
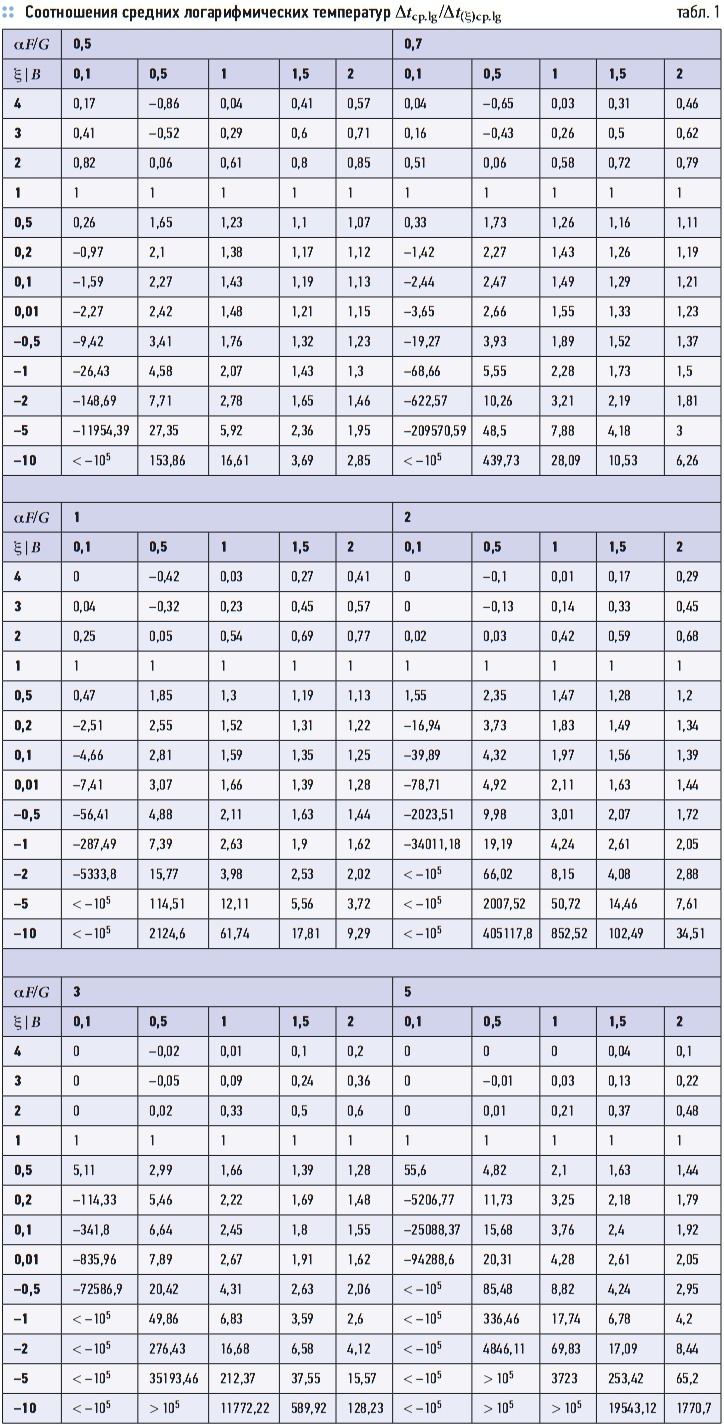
Табл. 1. Соотношения средних логарифмических температур Δtср.lg /Δt(ξ)ср.lg
В контактных аппаратах кондиционирования воздуха отсутствует четкая поверхность теплообмена, поэтому в этих случаях условные коэффициенты теплои массообмена вычисляются с использованием распространенных в практике зависимостей для средних логарифмических разностей. Так, для противоточного движения взаимодействующих сред:
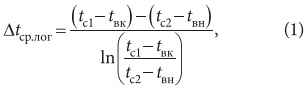
где tc1, tc2, tвк, tвн — температуры воздуха [°С] по сухому термометру и воды до и после взаимодействия в контактном аппарате, соответственно. Применение данной приведенной зависимости (1) для совместно протекающих процессов теплои массообмена вводит в расчеты одну существенную неточность, которая заключается в том, что подставляемые температуры по сухому термометру характеризуют только явное тепло, отдаваемое (воспринимаемое) воздухом, в то время как конечная температура воды tвк является результатом совместно протекающих процессов теплои массообмена и обусловливается полным теплообменом. Кроме того, эта зависимость выведена [1] в предположении соблюдения теплового баланса:
Gcpdtc = Wcвdtв, (2)
где G, W — весовой расход воздуха и распыляемой воды, кг/ч. При совместно протекающих процессах теплои массообмена в контактных аппаратах равенство (2) возможно только при неизменном влагосодержании воздуха. Однако эксперименты показывают, что осуществить такой процесс в контактном аппарате невозможно. Даже в том случае, когда начальные и конечные параметры воздуха лежат в i–d-диаграмме на одной и той же линии влагосодержания, реальный процесс изменения параметров воздуха по длине аппарата идет по кривой, отличной от линии d = const. Кроме того, обязательно следует заметить, что левая часть равенства (2) в общем случае теплои массообмена физически представляет собой количество явного тепла, отданного (воспринятого) воздухом (Qя), а правая часть — количество полного тепла воспринятого (отданного) водой. Рассматриваемое равенство не правомочно, так как в нем приравнивается различное по физическому смыслу тепло. Чтобы уравнение (2) было справедливым независимо от характера изменения параметров воздуха по длине контактного аппарата, воспользуемся понятием коэффициента увеличения теплообмена [2]:

И будем рассматривать процессы обработки воздуха, для которых ξ ≠ 0, то есть все, кроме адиабатических. Введем в правую часть уравнения (2) коэффициент увеличения теплообмена ξ. Тогда величина Wcвdtв/ξ будет характеризовать долю тепла, воспринятого водой за счет снижения температуры воздуха по сухому термометру. А получившееся выражение:

представляет собой ничто иное как уравнение теплового баланса по явному теплу, которое не зависит от направления осуществляемого процесса и характера изменения параметров воздуха и воды по длине контактного аппарата. Учитывая изложенное выше, осуществим вывод среднего температурного напора в контактных аппаратах установок кондиционирования воздуха. Известно, что в контактных аппаратах отсутствует строгая направленность движения взаимодействующих сред. Поэтому при выводе средних напоров теплосодержаний и температур обычно приравнивают к какому-то определенному типу движения. Для вывода выражения среднего температурного напора принимаем: движение воздуха и воды противоточное и поверхность теплообмена непрерывна (рис. 1). Выделим на данной поверхности обмена элементарную площадку. Количество явного тепла, переданного через эту площадку в единицу времени, определяется по закону Ньютона:
dQя = a(tc – tв)ξdF, (5)
где tc — температура воздуха по сухому термометру, °С; tв — температура воды, °С; a — коэффициент явного теплообмена, Вт/(м2⋅ч⋅°C). Количество полного тепла, передаваемого от воздуха к воде, можно определить при помощи аналогичного выражения, выведенного Меркелем в предположении наличия приближенной аналогии между процессами теплои массообмена:
dQn = σ(I – Iʺ в)ξdF. (6)
В результате взаимодействия с водой воздух понизит свою температуру на dtc, теплосодержание на dI, а вода повысит температуру на dtв. Следовательно:
dQя = –Gcpdtc; (7)
dQn = –GdI; (8)
dQn = Wcвdtв. (9)
Из (7) и (9) имеем:

где G — весовой расход воздуха, кг/ч; W — расход орошающей воды, кг/ч; cp, cв — весовые теплоемкости воздуха и воды [Вт/(кг⋅°C)], соответственно. Но из (3) следует, что:
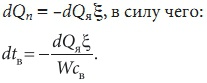
Учитывая, что разность дифференциалов равна дифференциалу разности, изменение температурного напора будет характеризоваться уравнением:
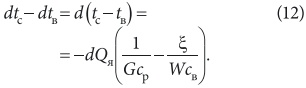
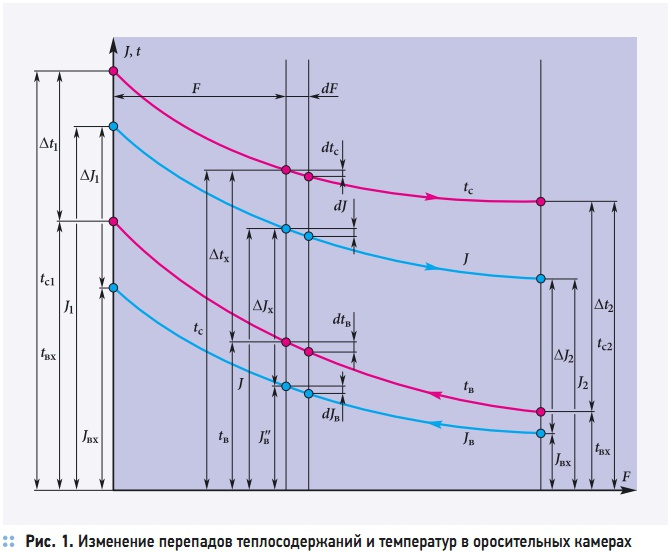
Водяной эквивалент воздуха постоянен, водяной эквивалент воды меняется с изменением параметров взаимодействующих сред ξ. Если принять ξ в (12) постоянным, то в результате получаем для среднего температурного напора выражение аналогичное общеизвестному выражению для среднелогарифмической разности температур. Но необходимо помнить, что оно справедливо только для одного определенного значения ξ, при котором отмечены данные температуры. При тех же температурах, но отличных ξ, будут другие значения средних температур. Это соответственно сказывается на величинах определяемых условных коэффициентов явного теплообмена. В табл. 1 для примера приведены соотношения средних логарифмических температур Δtср.lg/Δt(ξ)ср.lg (B — коэффициент орошения, кг/кг). Как видно из данных, приведенных в табл. 1, отличия средних температур при совместном протекании процессов теплои массообмена может достигать существенных величин и, следовательно, определенные по обычному выражению условные величины коэффициентов явного теплообмена будут также существенно отличаться друг от друга. Ниже сделана попытка определить средний температурный напор с учетом непостоянства водяного эквивалента воды. Для этого принимается отношение Льюиса [3] (α/σ = cp) справедливым на элементарной площадке обмена, и уравнение (12) можно записать в следующем виде:
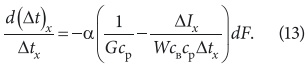
Мгновенное значение перепада теплосодержаний можно определить из экспоненциального закона изменения этой величины [4] ΔIx = ΔI1exp(–σmF), где: ΔI1 = I1 – Iʺ вк; m = (1/G – a/W), где I1 — теплосодержание влажного воздуха, поступающего в контактный аппарат; Iʺ вк — теплосодержание насыщенного воздуха при конечной температуре воды tвк; a — коэффициент пропорциональности между теплосодержанием насыщенного воздуха при температуре воды и теплосодержанием воды: a = Iʺ в/(cвtв). Чтобы привести уравнение (13) к виду, удобному для интегрирования, вводим новую переменную y = Δtxexp(σmF), далее, принимая α и σ постоянными, независящими от параметров взаимодействующих сред, интегрируя в пределах от y0 = Δt1 при F = 0 до y = Δtexp(σmF) при F = F, получаем:
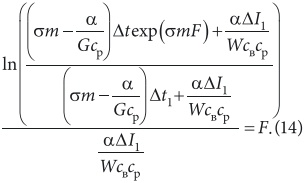
Откуда нетрудно установить особенности изменения температурного напора вдоль поверхности теплои массообмена при контакте воздуха с водой в контактных аппаратах кондиционирования:
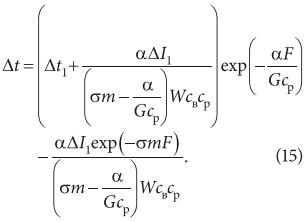
Из данной зависимости следует, что температурный напор изменяется не по экспоненте, а является сложной функцией. Причем, характер изменения температурного напора обусловливается начальным температурным напором Δt1, начальным напором теплосодержаний ΔI1, характером изменения напора теплосодержания и соотношением количеств взаимодействующих сред. Зная закон изменения температурного напора на основании теоремы о среднем при постоянстве коэффициентов теплои массообмена получаем следующее выражение для среднего значения температурного напора:
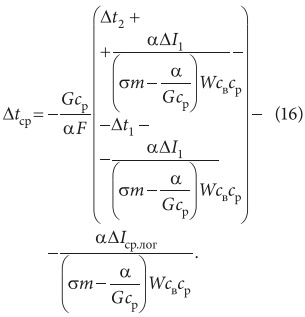
После некоторых математических преобразований получаем компактную зависимость для среднего значения температурного напора [5]:
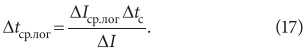
Аналогичная зависимость получается и для случая прямоточного движения взаимодействующих сред. Следуя изложенной выше последовательности несложно установить и подобного вида зависимости для средних напоров массообмена (влагосодержаний и т.п.). Они имеют следующий вид: