При движении воздушного потока в воздуховодах и каналах систем вентиляции и кондиционирования воздуха (В и КВ), кроме потерь давления на трение, существенную роль играют потери на местных сопротивлениях — фасонных частях воздуховодов, воздухораспределителях и сетевом оборудовании.
Такие потери пропорциональны динамическому давлению рд = ρv²/2, где ρ — плотность воздуха, примерно равная 1,2 кг/м³ при температуре около +20 °C; v — его скорость [м/с], определяемая, как правило, в сечении канала за сопротивлением.
Коэффициенты пропорциональности ξ, называемые коэффициентами местного сопротивления (КМС), для различных элементов систем В и КВ обычно определяются по таблицам, имеющимся, в частности, в [1] и в ряде других источников. Наибольшую сложность при этом чаще всего вызывает поиск КМС для тройников или узлов ответвлений. Дело в том, что в этом случае необходимо принимать во внимание вид тройника (на проход или на ответвление) и режим движения воздуха (нагнетание или всасывание), а также отношение расхода воздуха в ответвлении к расходу в стволе L´о = Lo/Lc и площади сечения прохода к площади сечения ствола F´п = Fп/Fс.
Для тройников при всасывании нужно учитывать ещё и отношение площади сечения ответвления к площади сечения ствола F´о = Fо/Fс. В руководстве [1] соответствующие данные приведены в табл. 22.36–22.40. Однако при проведении расчётов с использованием электронных таблиц Excel, что в настоящее время достаточно распространено в связи с широким использованием различного стандартного программного обеспечения и удобством оформления результатов вычислений, желательно иметь аналитические формулы для КМС, по крайней мере, в наиболее часто встречающихся диапазонах изменения характеристик тройников.
Кроме того, это было бы целесообразно в учебном процессе для сокращения технической работы обучающихся и переноса основной нагрузки на разработку конструктивных решений систем.
Подобные формулы имеются в таком достаточно фундаментальном источнике, как [2], но там они представлены в весьма обобщённом виде, без учёта особенностей конструкции конкретных элементов существующих вентиляционных систем, а также используют значительное число дополнительных параметров и требуют в ряде случаев обращения к определённым таблицам. С другой стороны, появившиеся в последнее время программы для автоматизированного аэродинамического расчёта систем В и КВ используют некоторые алгоритмы для определения КМС, но, как правило, они неизвестны для пользователя и могут поэтому вызывать сомнения в своей обоснованности и корректности.
Также в настоящее время появляются некоторые работы, авторы которых продолжают исследования по уточнению расчёта КМС или расширению диапазона параметров соответствующего элемента системы, для которых полученные результаты будут справедливы. Данные публикации возникают как в нашей стране, так и за рубежом [3–8], хотя в целом их число не слишком велико, и основываются преимущественно на численном моделировании турбулентных потоков с помощью ЭВМ или на непосредственных экспериментальных исследованиях. Однако полученные авторами данные, как правило, трудно использовать в практике массового проектирования, поскольку они пока не представлены в инженерном виде.
В связи с этим представляется целесообразным анализ данных, содержащихся в таблицах [1], и получение на их основе аппроксимационных зависимостей, которые имели бы по возможности наиболее простой и удобный для инженерной практики вид и одновременно достаточно адекватно отражали бы характер имеющихся зависимостей для КМС тройников. Для наиболее часто встречающихся их разновидностей — тройников на проходе (унифицированных узлов ответвлений) данная задача была решена автором в работе [9]. В то же время для тройников на ответвлении аналитические соотношения найти труднее, поскольку сами зависимости здесь выглядят более сложно. Общий вид аппроксимационных формул, как и всегда в подобных случаях, получается исходя из расположения расчётных точек на поле корреляции, а соответствующие коэффициенты подбираются методом наименьших квадратов с целью минимизации отклонения построенного графика средствами Excel. Тогда для некоторых наиболее употребительных диапазонов Fп/Fс, Fо/Fс и Lо/Lс можно получить выражения:
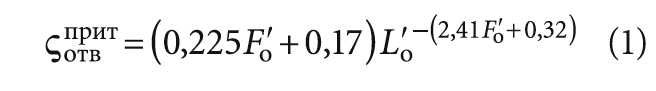
при L´о = 0,20–0,75 и F´о = 0,40–0,65 — для тройников при нагнетании (приточных);
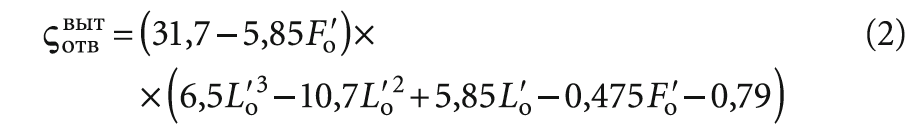
при L´о = 0,2–0,7, F´о = 0,3–0,5 и F´п = 0,6–0,8 — для тройников при всасывании (вытяжных).
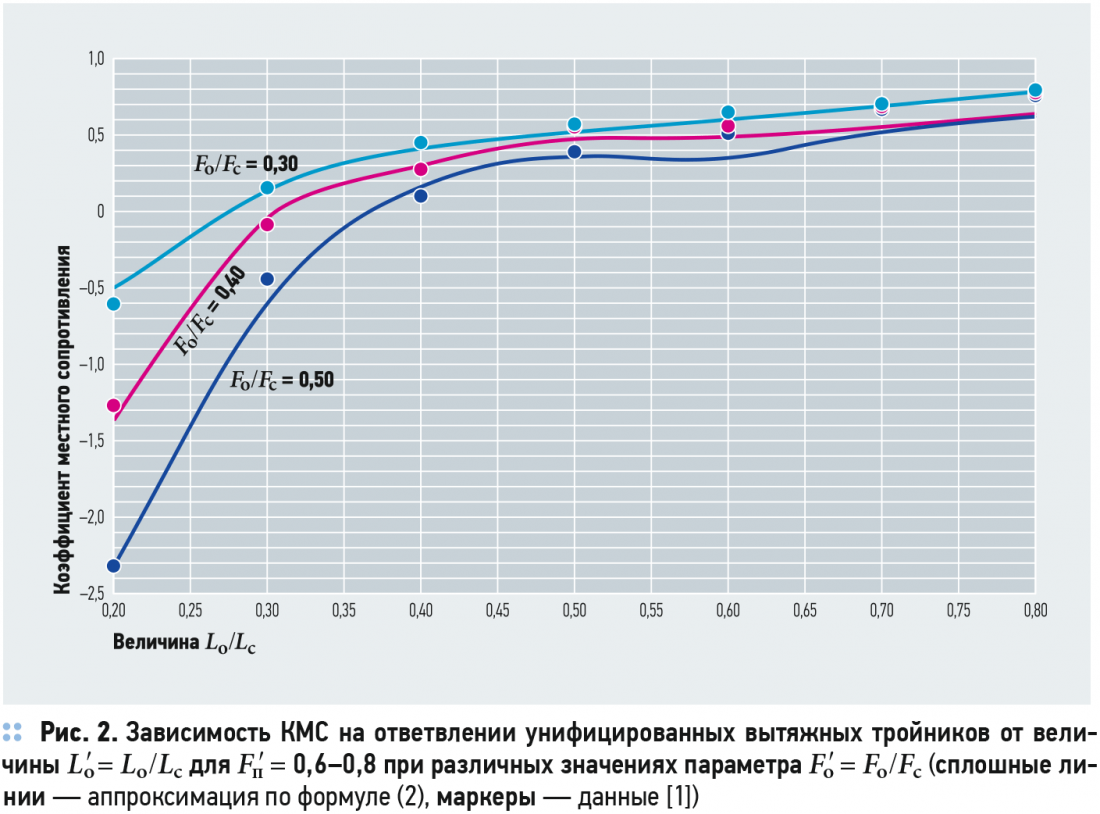
Точность зависимостей (1) и (2) демонстрируют рис. 1 и 2, где приведены результаты обработки табл. 22.36 и 22.37 [1] для КМС унифицированных тройников (узлов ответвлений) на ответвлении круглого сечения при всасывании. В случае прямоугольного сечения результаты будут отличаться несущественно.
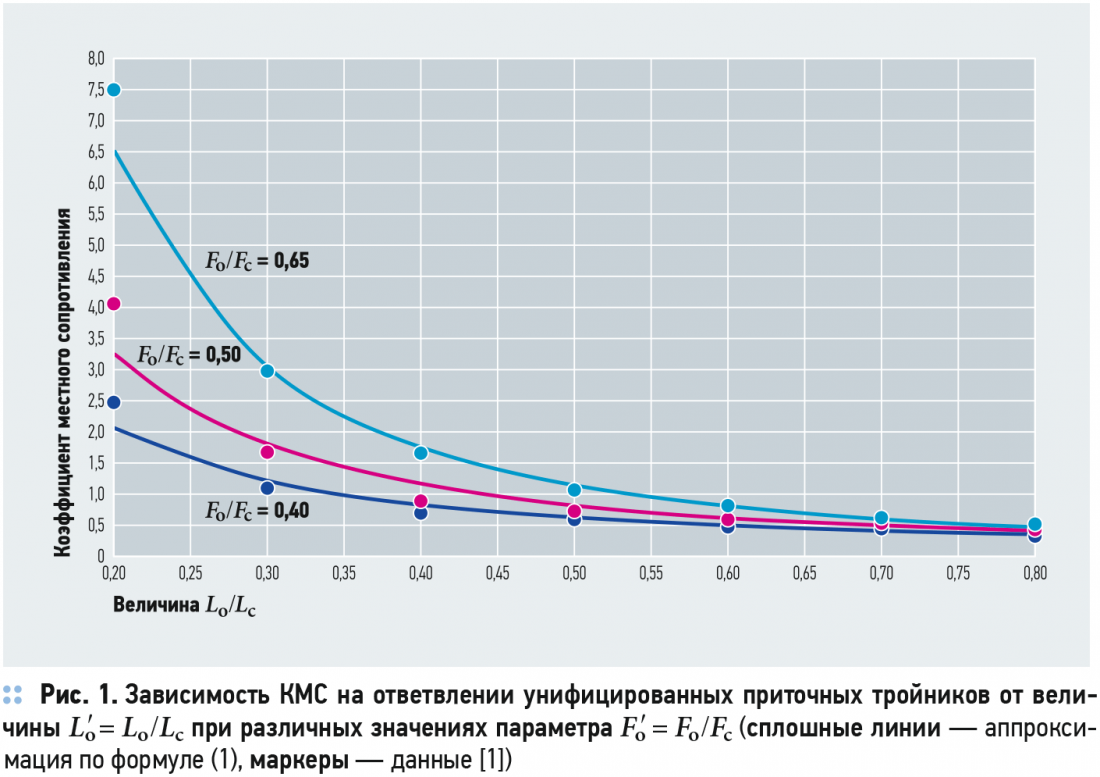
Можно отметить, что расхождение здесь больше, чем для тройников на проход [9], и составляет в среднем 10– 15 %, иногда даже до 20 %, но для инженерных расчётов это может быть допустимым, особенно с учётом очевидной исходной погрешности, содержащейся в таблицах [1], и одновременного упрощения расчётов при использовании Excel. В то же время полученные соотношения не требуют никаких иных исходных данных, кроме уже имеющихся в таблице аэродинамического расчёта. В самом деле, в ней в явном виде должны быть указаны и расходы воздуха, и сечения на текущем и на соседнем участке, входящие в перечисленные формулы. В первую очередь это упрощает вычисления при применении электронных таблиц Excel. Одновременно рис. 1 и 2 позволяют убедиться, что найденные аналитические зависимости вполне адекватно отражают характер влияния всех основных факторов на КМС тройников и физическую сущность происходящих в них процессов при движении воздушного потока.
При этом формулы, приведённые в настоящей работе, весьма просты, наглядны и легко доступны для инженерных расчётов, особенно в Excel, а также в учебном процессе. Их использование позволяет отказаться от интерполяции таблиц при сохранении точности, требуемой для инженерных расчётов, и непосредственно вычислять коэффициенты местного сопротивления тройников на ответвлении в весьма широком диапазоне отношений сечений и расходов воздуха в стволе и ответвлениях.
Этого вполне достаточно для проектирования систем вентиляции и кондиционирования воздуха в большинстве жилых и общественных зданий.

























