Обобщённый подход к расчёту гидравлических сетей

Введение

Гидравлическими сетями традиционно называют трубопроводные системы, предназначенные для транспортировки несжимаемых жидкостей. Такими «жидкостями» являются в том числе и газы при скоростях движения, существенно меньших скорости звука. Решение задачи о распределении потоков между отдельным элементами гидравлической сети является неотъемлемой частью моделирования её работы.

Нелинейная система уравнений, описывающая движение жидкости в такой сети, включает уравнения двух типов: баланса массы и механической энергии (уравнения Кирхгофа). Даже в случае относительно простых сетей количество уравнений этой системы велико, и до изобретения компьютеров её решение было весьма трудоёмким.

Вероятно, первыми инженерами, которые столкнулись с необходимостью решения таких задач, были специалисты в области проектирования и эксплуатации распределительных сетей водоснабжения. Неудивительно, что к концу ХХ века, когда компьютеры стали основными рабочими инструментами инженеров, были разработаны эффективные алгоритмы решения систем уравнений сетей водоснабжения и большое количество реализующих их программ.

Другой группой гидравлических сетей являются системы вентиляции различного назначения. Размерность таких сетей обычно существенно меньше, чем сетей водоснабжения. Чаще всего это разветвляющиеся системы с известными расходами воздуха в их отдельных участках. Отсутствие кольцевых соединений значительно упрощает расчёт, который часто не требует использования сложных алгоритмов и специального программного обеспечения для их реализации. Такие задачи в теории гидравлических цепей относят к классу прямых. Именно они и решаются с помощью подавляющего большинства программ для проектирования систем вентиляции, представленных на рынке.

Увеличение этажности зданий, применение новых конструкционных элементов и материалов, устройство «тёплых» чердаков и т.д. — это лишь некоторые причины, приводящие к усложнению аэродинамических расчётов систем вентиляции. Проектировщики всё чаще вынуждены решать не только прямые, но и более сложные обратные задачи об определении фактических расходов воздуха в различных частях систем вентиляции.

Недостаточно полный учёт факторов, влияющих на работу вентиляции, приводит к тому, что система в лучшем случае не позволит обеспечить качественное проветривание помещений при некоторых сочетаниях параметров наружного и внутреннего воздуха. В худшем случае система «опрокидывается», когда в то или иное помещение через вентиляционные каналы начинает поступать воздух из других помещений (квартир), принося с собой в том числе и неприятные запахи.

В ряде случаев нарушение санитарных норм воздухообмена может явиться веской причиной для обращения жителей в судебные инстанции, которые всё чаще встают на сторону истцов, вынося решения о необходимости улучшения работы вентиляции в уже существующем здании. В таких случаях возникает непростая задача построения математической модели системы, учитывающей реальные условия её эксплуатации. Только такая модель после выполнения многовариантных расчётов позволяет найти оптимальное решение возникших проблем.

Далее будет показано, что моделирование работы систем вентиляции различных видов можно успешно выполнять с помощью программ, изначально предназначенных для расчёта сетей водоснабжения. Такие программы сейчас обладают очень большими возможностями, которые для решения поставленной выше задачи даже избыточны. Достаточно, чтобы программа позволяла построить схему сети непосредственно на экране компьютера, автоматически составляла для неё систему уравнений Кирхгофа и решала её.

Этими функциями обладают все программы для расчёта сетей водоснабжения, в том числе и свободно распространяемая программа EPANET, в которой реализован градиентный метод решения уравнений Кирхгофа (Global Gradient Algorithm, GGA), сочетающий быстроту поиска решения и высокую точность [1]. Особенностью этого и подобных ему алгоритмов является то, что до начала расчётов расходы и направления течения жидкости считаются неизвестными.

Таким образом, при его использовании для расчёта систем вентиляции появляется возможность выявления участков сети, в которых направления течений отличаются от проектных.

Расчёт системы вентиляции в среде EPANET

Прежде всего необходимо иметь в виду, что, поскольку программа EPANET предназначена для расчёта сетей водоснабжения, в ней используются соответствующая терминология и единицы измерения величин. Например, вполне очевидно, что в вентиляционных сетях функции насосов выполняют вентиляторы, а вместо метров водяного столба в качестве единиц измерения напоров придётся использовать метры столба воздуха с заданной температурой.

Плотность воды — практически неизменная величина, поэтому и плотность воздуха также придётся считать одинаковой во всех частях сети. Это, в частности, означает, что изменение температуры воздуха при движении через окна, приточные клапаны и другие подобные элементы не учитывается. Одинаковой придётся считать плотность и во всех воздуховодах. Это ограничение, очевидно, сужает круг задач (видов систем вентиляции), которые могут быть решены с помощью предлагаемой методики. В то же время при аэродинамических расчётах систем естественной и гибридной вентиляции такое приближение вполне допустимо и используется при традиционных методах проектирования [2].

Решение задачи начинается с построения схемы сети. Схема сети водоснабжения на экране чаще всего выглядит так же, как и реальная. В случае системы вентиляции её расчётную схему сначала необходимо представить в виде графа [3]. На рис. 1 показана расчётная схема простой системы естественной вентиляции и соответствующий ей граф.

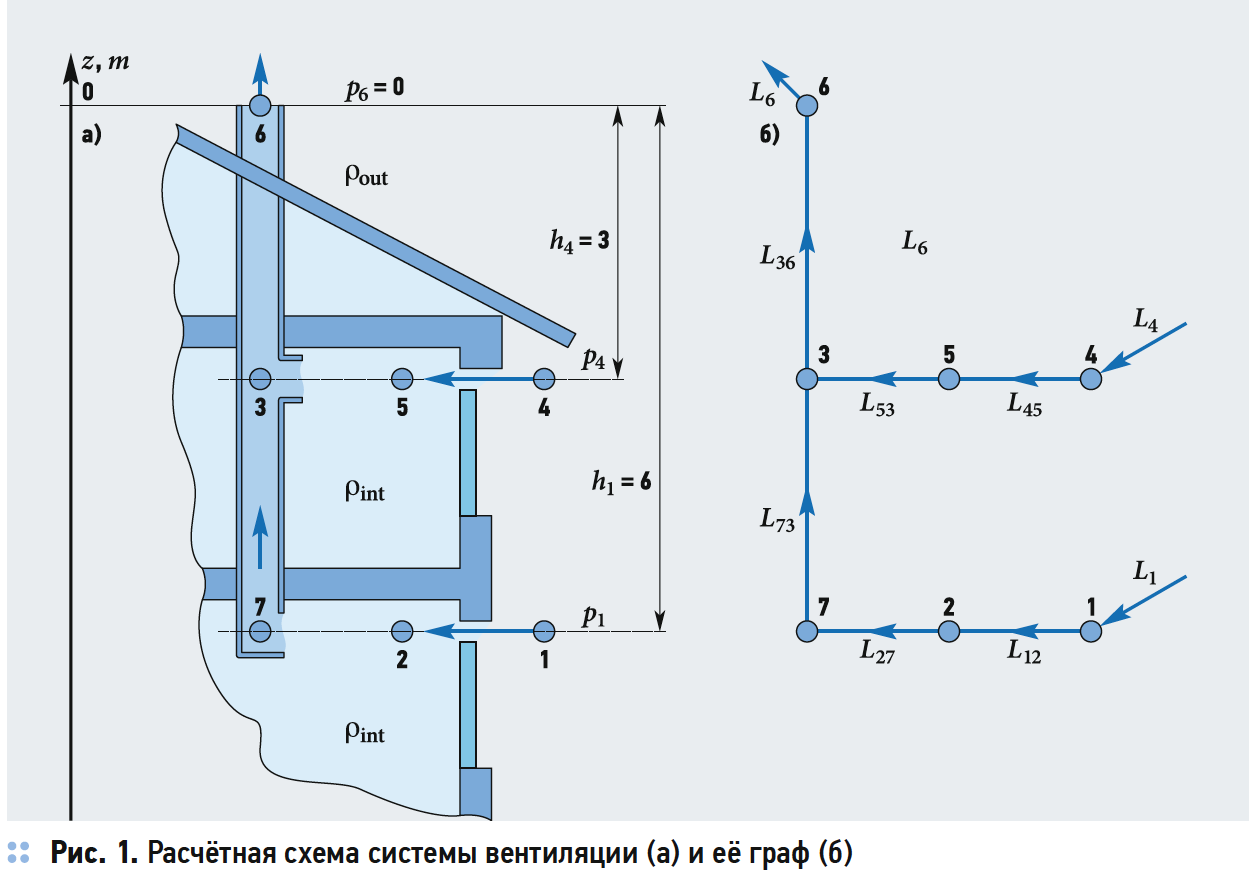
Как видно, граф сети — это схема движения воздушных потоков, состоящая из элементов двух типов: узлов и ветвей.

Узлы бывают двух видов: граничные и внутренние. Через граничные узлы воздух поступает в сеть или удаляется из неё. Такими узлами являются первый, четвёртый и шестой (рис. 1). В EPANET граничные узлы называются резервуарами. Их единственной характеристикой является высота z, отсчитываемая от общей для всех узлов плоскости сравнения.

В сетях водоснабжения высота узларезервуара (точнее, уровня воды в нём) — это геометрический параметр. При расчётах систем вентиляции эти высоты необходимо предварительно откорректировать в зависимости от соотношения плотностей наружного и внутреннего воздуха ρout и ρint, соответственно.

Система уравнений Кирхгофа для рассматриваемой сети имеет вид:

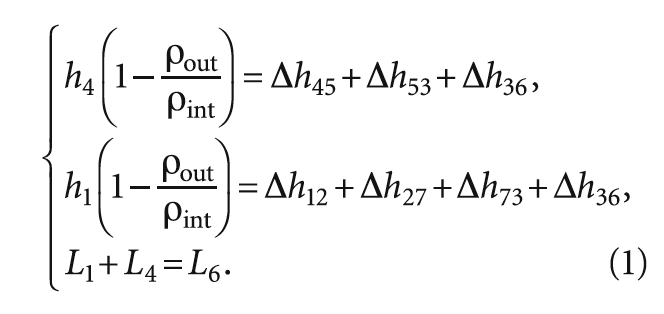
здесь Δ_hij — сумма местных и линейных потерь напора жидкости с плотностью ρ_int при её движении от узла i к узлу j. Зависимости потерь напора от расходов L_ij в соответствующих ветвях считаются заданными. Их вид для капельных жидкостей и газов, очевидно, одинаковый.

Наиболее существенно то, что при составлении данной системы принята во внимание связь между давлениями pi в граничных узлах №№1, 4 и 6 через основной закон гидростатики.

Если жидкость в сосудах и трубопроводе капельная, то ρout << ρint, и выражения в скобках в левых частях уравнений близки к единице. Именно так и получается при расчётах сетей водоснабжения.

Если же обе «жидкости» представляют собой воздух с различными плотностями, то при ρ_out > ρ_int выражение в скобках будет отрицательным. То есть внутренняя жидкость под действием внешнего (гравитационного) давления должна двигаться снизу вверх, как это и происходит при работе естественной вентиляции.

Введём обозначение корректирующего множителя для высот граничных узлов-резервуаров z:

Например, если плотности воздуха ρ_out = 1,27 кг/м³, а ρ_int = 1,20 кг/м³, что соответствует температурам +5 и +20 °C, то A = – 0,05833.

Расчётные высоты расположения граничных узлов-резервуаров z_i:

Знак z определяется положением плоскости сравнения, на которой величина избыточного давления принимается равной нулю. В частности, при A < 0 для схемы на рис. 1 при выборе плоскости сравнения на уровне узла №6 z > 0.

Если необходимо учесть ветровое давление, то его величину, выраженную в метрах столба воздуха с плотностью ρint, необходимо добавить к высоте z с соответствующим знаком.

Внутренние узлы соответствуют отдельным помещениям задания (квартира, чердак и т.п.), а также точкам слияния или разделения потоков (тройник, крестовина). В общем случае параметрами внутренних узлов являются пьезометрические напоры и узловые отборы жидкости.

Пьезометрические напоры во внутренних узлах определяются EPANET в ходе расчёта. Их значения не зависят от вертикальных координат узлов и в случае вентиляционных систем обычно не представляют интереса.

Узловыми отборами являются расходы жидкости, удаляемой из системы. В случае систем водоснабжения их значения очень важны, поскольку это именно те расходы воды, которые поступают к потребителям. В вентиляционных системах таких потребителей обычно нет, и узловые отборы равны нулю. Если всётаки в каких-либо узлах отборы существуют, необходимо иметь в виду, что их величины в программе EPANET условно считаются положительными. Если же жидкость втекает в узел, то заданный расход вводят со знаком «минус».

Узлы графа соединяются друг с другом ветвями (рёбрами). Внутри каждой ветви жидкость (газ) движется с неизменным расходом, при этом происходит изменение её напора. EPANET позволяет использовать три вида ветвей. Два из них (трубопроводы и задвижки) используются для моделирования всевозможных гидравлических сопротивлений.

Характеристиками трубопровода являются длина, диаметр, коэффициент местных гидравлических сопротивлений, шероховатость стенок. С их помощью моделируются вентиляционные каналы, а также те элементы, для которых коэффициент местного сопротивления неизменный (не зависит от скорости жидкости).

При расчётах систем вентиляции в качестве диаметра ребра графа нужно вводить диаметр трубы эквивалентной площади.

Традиционная методика расчёта потерь давления на трение в воздуховодах основана на использовании специальных номограмм и поправочных коэффициентов, учитывающих величину эквивалентной шероховатости стенок. При использовании EPANET расчёт приходится выполнять по методу Дарси-Вейсбаха, то есть с использованием коэффициента трения. Его величина определяется программой автоматически.

Необходимо подчеркнуть, что при использовании EPANET все воздуховоды считаются круглыми. Воздуховоды реальных сетей очень часто имеют прямоугольные сечения. Формальная замена прямоугольного воздуховода на круглый той же площади в ряде случаев может привести к существенной ошибке при расчёте линейных потерь давления.

При сооружении современных систем вентиляции жилых зданий широко используются различные приточные и вытяжные устройства (клапаны). В таких системах потери давления в вентиляционных каналах, часто оказываются малыми по сравнению с потерями давления в местных сопротивлениях. Оценить влияние линейных потерь на расходы воздуха в отдельных частях системы можно, если выполнить расчёты при различных значениях эквивалентной шероховатости поверхностей вентканалов.

Другим способом моделирования, как трубопроводов, так и любых иных элементов системы, является использование ветвей-задвижек. Этим термином в EPANET обозначаются любые сопротивления с заданными в табличной форме зависимостями падения давления от расхода.

Третьим видом ветвей графа являются нагнетатели (насосы и вентиляторы), в которых давление потока жидкости увеличивается. Расходно-напорные характеристики нагнетателей в EPANET также задаются в виде таблиц. Удобно то, что характеристики нагнетателей и задвижек можно хранить в виде общей библиотеки.

Вернёмся к рассматриваемому примеру (рис. 1). Определим расходы воздуха, поступающего в помещения через оконные приточные клапаны при некоторых конкретных значениях параметров элементов сети.

Зададим для определённости зависимость расходов воздуха L [м³/ч] от перепада давления Δр [Па] на приточных клапанах (ветви графа 1–2 и 4–5) в виде функции [4]:

L = 7,75(Δp)^0,522. (4)

При расчётах будем учитывать местные потери давления в вентиляционных решётках и при входе в вентиляционный канал с поворотом потока (ветви графа 2–7 и 3–5) с суммарным коэффициентом местных сопротивлений ξ = 4.

Вентиляционные каналы (ветви графа 7–3 и 3–6) имеют размеры 120×220 мм. Коэффициенты трения в каналах λ = 0,034, что приблизительно соответствует абсолютной эквивалентной шероховатости стенок 1,7 мм. При расчёте потерь давления на отрезке 3–6 учтём потери энергии при истечении воздуха в окружающее пространство с коэффициентом местного сопротивления ξ = 1.

Температуры наружного и внутреннего воздуха будут равняться +5 и + 20 °C, соответственно.

В результате точного решения системы уравнений (1) получим расходы L1 = 15,74 м³/ч и L4 = 10,87 м³/ч.

Расчётная схема той же сети в среде EPANET показана на рис. 2. Участки 1–2 и 4–5 на данном рисунке моделируются задвижками с характеристиками, описываемыми формулой (4).

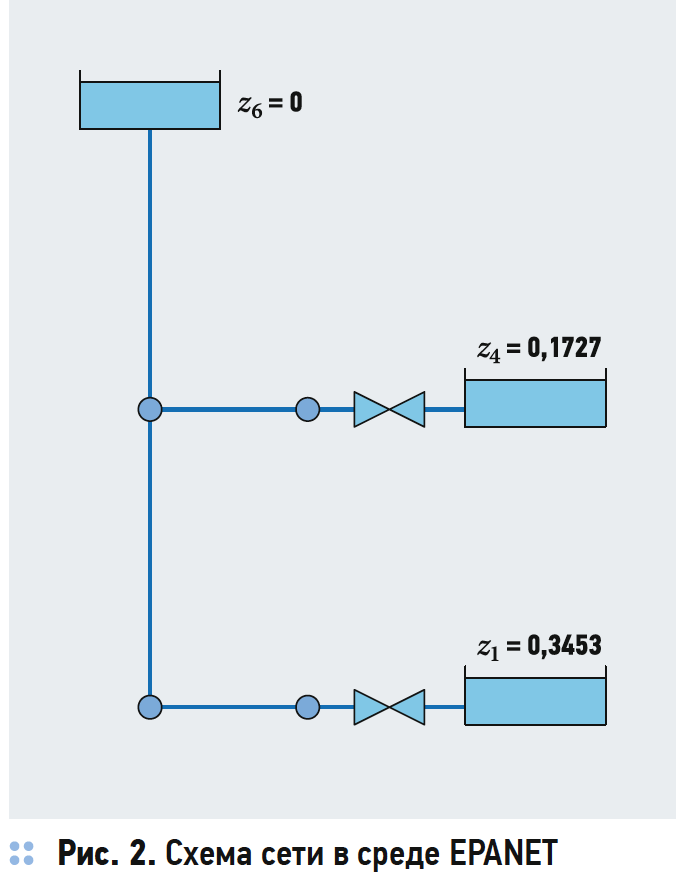
Поскольку при использовании программы EPANET характеристики отдельных элементов приходится вводить в виде таблиц, а не формул типа (4), возникает ошибка интерполяции. В нашем случае характеристика была задана в виде таблицы из восьми точек в диапазоне изменения L от нуля до 45 м³/ч. В результате расчёта оказалось, что найденные расходы отличаются от точного решения менее чем на 1 %.

EPANET предоставляет возможность моделировать работу сети не только при любых сочетаниях наружных и внутренних параметров воздуха, но и найти решения, способствующие улучшению работы вентиляции. Например, в нашем случае увеличение воздухообмена может быть достигнуто с помощью общего вытяжного вентилятора, установленного на участке 3–6.

Для определения рабочей точки вытяжного вентилятора при требуемой величине воздухообмена в программной среде EPANET достаточно выполнить несколько последовательных расчётов, постепенно уменьшая высоту резервуараисточника z6.

Например, при z₆ = – 1 м расходы воздуха составят L₁ = 31,8 и L₄ = 29,5 м³/ч.

Такие параметры могут быть достигнуты с помощью вентилятора, обеспечивающего подачу около 60 м³/ч при давлении порядка 12 Па.

Данная методика была проверена при расчётах систем вентиляции нескольких видов, рассматриваемых в руководстве [4]: с естественным побуждением, с децентрализованным механическим удалением воздуха с «тёплого» чердака и с централизованным удалением воздуха. Во всех случаях результаты расчётов с применением EPANET полностью соответствуют приводимым данным.

Заключение

Показано, что практически любая из имеющихся сейчас программ для расчёта сетей водоснабжения, среди которых имеются и свободно распространяемые, может использоваться и при проектировании систем естественной и гибридной вентиляции. При этом не только обеспечивается необходимая точность расчётов, но и существенно уменьшается время их выполнения. Это особенно важно в тех случаях, когда требуется смоделировать работу системы при различных сочетаниях параметров внутреннего и наружного воздуха, а также при поиске наилучших конструктивных решений, обеспечивающих надёжную и устойчивую работу системы вентиляции.