
Рис. 1. Номограмма для определения x/L
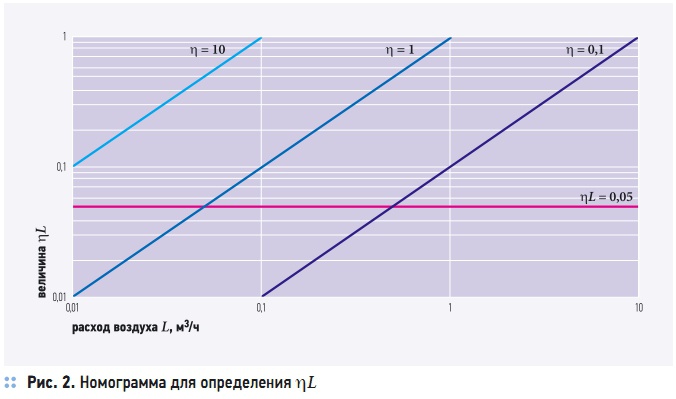
Рис. 2. Номограмма для определения ηL
Безопасность персонала, занятого на промышленных предприятиях, в значительной мере обеспечивается за счет поддержания нормируемых параметров воздушной среды средствами вентиляции. Для перемещения по вентиляционной сети требуемого расхода воздуха вентиляторы совершают определенную работу, поддерживая некоторое давление, необходимое для преодоления ее сопротивления. В общем случае для вентиляционной сети существует взаимосвязь:
P = RLn , (1)
где P — полное давление, которое необходимо для перемещения воздуха в сети, Па; L — расход воздуха, м3/с; n — показатель степени, зависит от режима движения воздуха, при турбулентном режиме n = 2, при ламинарном n = 1; R — аэродинамическое сопротивление вентиляционной сети. В многочисленных работах по рудничной вентиляции, где в горных выработках отмечается в основном турбулентный режим движения воздуха, при отсутствии гидростатических составляющих давления уравнение (1) представляют следующем в виде: P = RL2 . (2) При этом величина R однозначно определяется как аэродинамическое сопротивление соответствующего участка горной выработки или шахты в целом [1–10]. Ее размерность, как это следует из уравнения (2):
[R] = [P] / [L2 ]. (3)
Если давление измеряют в кг/м2 (мм водн. ст.), а расход воздуха — в м3/с, то размерность аэродинамического сопротивления тогда составит:
[R] = (кг⋅с2)/м8. (4)
Если давление измеряют в единицах системы СИ (Па), то размерность аэродинамического сопротивления:
[R] = (Па⋅с2)/м6 = (Н⋅с2)/м8. (5)
Из сравнения (4) и (5) следует, что 1 кμ = 9,81 Па⋅с2/м6. К сожалению, в литературе по промышленной вентиляции четкое и единое определение аэродинамического сопротивления вентиляционных каналов отсутствует. Различные авторы трактуют его разнообразно. Так, авторы работы [11, с. 75] пишут: «…Аэродинамическое сопротивление ΔP участка или элемента вентиляционной сети определяется как разница полных давлений в начале P1 и конце P2 участка: ΔP = P1 – P2…».
В работе [12, с. 119] утверждается: «…Сопротивление модели сети — разность абсолютных давлений в камере и атмосферного, то есть сопротивление модели равно измеренному в камере избыточному давлению…». А, например, М.Д. Сидоров [13, c. 19] пишет следующее: «…Подача вентилятором воздуха в сеть определяется ее сопротивлением, равным давлению, развиваемому вентилятором…».
Эти утверждения являются ошибочными, так как аэродинамическое сопротивление вентиляционной сети или ее отдельного участка и величина полного давления, необходимого для преодоления этого сопротивления, есть совершенно разные по своей природе физические величины, а размерность аэродинамического сопротивления отличается от размерности давления, и даже косвенная его характеристика по величине падения давления на нем не может однозначно определять величину R, поскольку при этом необходимо указывать еще и расход воздуха. В работах [14–20] уравнение (2) представляется в виде:
P = kL2 , (6)
где k — коэффициент, который в цитируемых работах несет разные смысловые нагрузки. Так, по данным [14] k — это коэффициент сопротивления сети или отдельных элементов, может быть представлен как сопротивление при перемещении объема в 1 м3/ч и измеряется в единицах давления. В соответствии с работой [15, с. 21] k — это коэффициент, зависящий от конфигурации сети и параметров перемещаемого газа.
Например, М.П. Калинушкин [16, c. 65] утверждает, что коэффициент k зависит главным образом от геометрических размеров сети. По данным работы [17, c. 296] коэффициент k — постоянный для данной сети коэффициент. В работе [18, c. 60] отмечается, что k — это коэффициент, характеризующий способность сети оказывать сопротивление проходящему по ней воздуху.
В соответствии с работой [19, c. 19] k — это коэффициент пропорциональности, характеризующий гидравлическое сопротивление потоку, оказываемое сетью, и зависящий от формы участков сети, состояния их поверхностей, плотности и вязкости газа, а также числа Re. С.Е. Бутаков [20, c. 165] отмечает, что «…коэффициент k назван характеристикой сопротивляемости трубы или просто характеристикой…».
В работе [21] аналогичный коэффициент обозначен через α, который расшифрован как «корреляционный коэффициент». Такой разнобой в трактовке одной и той же величины аэродинамического сопротивления вентиляционной сети указывает на отсутствие точной терминологии и свидетельствует о целесообразности ее корректировки. Одним из важных элементов вентиляционной сети является фильтрующее устройство.
Оно обычно имеет большую поверхность фильтрации, поэтому скорости просачивания воздуха через фильтрующий элемент оказываются малыми, и при движении воздуха через фильтр преобладает ламинарный режим. В соответствии с уравнением (1) n = 1, и величина аэродинамического сопротивления фильтра определяется по данным инструментальных замеров падения давления на фильтре ΔP и расхода воздуха через него L:
Rф = ΔP/L. (7)
Размерность Rф, как это следует из выражения (7), (Па⋅с)/м3. К сожалению, в технической литературе по фильтрующим устройствам [22– 27] и даже в справочниках [13, 28, 29, 30] и учебниках [14, 31] аэродинамическое сопротивление фильтров также оценивают в единицах давления, что допустимо только для частного случая — при заданных L и ΔP для установления допустимых значений второго при известном первом. С учетом особенностей геометрии каналов фильтра в общем случае падение давления на нем можно представить в виде следующей суммы:
ΔPф = R1L + R2L, (8)
где R1 и R2 — соответственно, линейная и квадратичная составляющие аэродинамического сопротивления фильтра. Полученное уравнение (8) может использоваться и в других элементах рассматриваемой вентиляционной сети для оценки их аэродинамического сопротивления, если режим движения воздуха не соответствует строго ламинарному или турбулентному режимам. Запишем далее уравнение (8) в следующем виде:

Оценим возможность применения квадратичного закона сопротивления, допуская погрешность оценки ΔP не более 5 %. В этом случае второе слагаемое в скобках правой части уравнения (9) не должно превышать 0,05. Как следует из номограммы (рис. 1), этому условию будут соответствовать значения расходов воздуха L > 2 м3/с при x = 0,1, L > 20 м3/с при x = 1 и L > 200 м3/с при x = 10, то есть с уменьшением соотношения линейной и квадратичной составляющих аэродинамического сопротивления область возможной аппроксимации закона сопротивления квадратичным выражением, как видно, расширяется. Аналогичные выкладки для линейного закона сопротивления дает следующее выражение:

Как следует из рис. 2, возможность применения линейного закона сопротивления, допуская при этом погрешность оценки ΔP не более 5 %, возможна в диапазоне расходов воздуха L < 0,005 м3/с при η = 10, L < 0,05 м3/с при η = 1 и L < 0,5 м3/с при η = 0,1, то есть с уменьшением соотношения квадратичной и линейной составляющих аэродинамического сопротивления расширяется область возможной аппроксимации закона сопротивления линейным выражением.
Выводы
- Аэродинамическое сопротивление вентиляционной сети или ее отдельного элемента — это физическая величина, которая может быть определена расчетным путем на основе известных данных о геометрических размерах вентиляционного сооружения, коэффициенте сопротивления трения и режиме движения воздуха.
- Характеризовать аэродинамическое сопротивление вентиляционной сети или ее отдельного элемента по величине падения давления на его преодоление правомерно только в частных случаях при обязательном фиксировании расхода воздуха через рассматриваемое сопротивление.
- Если в вентиляционной сети в целом или на отдельных ее участках имеет место промежуточный режим движения воздуха (1 ≤ n ≤ 2), то следует использовать двучленный закон сопротивления, определяя, соответственно, линейную и квадратичную составляющие аэродинамического сопротивления.
























