
В оборудовании различного назначения с успехом применяются теплообменные аппараты, содержащие сферические элементы. Достаточно подробно исследованы процессы теплообмена при обтекании таких элементов потоком теплоносителя энергетической установки [1, 2]. При этом в качестве сферических элементов рассматривались объекты без фазовых переходов внутри них. Представляет интерес оценка влияния на температуру обтекающего потока фазопереходных процессов (плавление, парообразование, затвердевание и конденсация) внутри сферических капсул. Такие капсулы применимы для тепловых накопителей (ТН).
Постановка задачи
Рассмотрим задачу в следующей постановке: сферическая капсула заполнена плавящимся теплоаккумулирующим материалом (ТАМ) — обычно это смесь солей щелочных металлов или кристаллогидраты неорганических солей, но для нашей задачи это неважно; она обтекается потоком горячего теплоносителя; внутри капсулы давление постоянно (рис. 1).
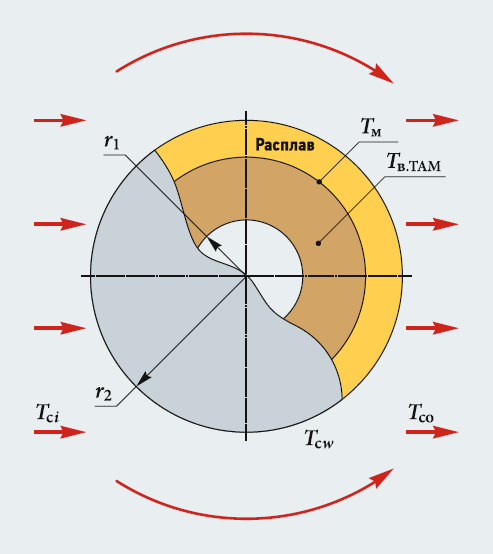
Рис. 1. Схема рассматриваемой задачи о сферической капсуле с плавящимся теплоаккумулирующим материалом
Необходимо оценить влияние процесса переноса теплоты на температуру обтекающего потока.
Набегающий на сферу поток теплоносителя имеет температуру Tci. Температура ТАМ — TТАМ, граница фазового перехода перемещается от внешнего диаметра к внутреннему.
Моделирование
Температура обтекающего потока теплоносителя за сферической капсулой [3]:
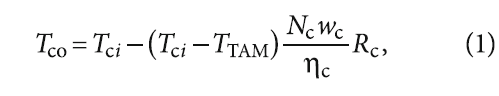
где Nc — безразмерное число теплопередачи; wc — безразмерная скорость передвижения границы фазового перехода; ηc — энергетический коэффициент полезного действия; Rc — коэффициент формы капсулы.
Безразмерное число теплопередачи зависит от числа теплопередачи Kc, площади поверхности теплообмена F(r1), секундного массового расхода обтекающего ячейку потока mc и его удельной теплоёмкости cp:

В свою очередь, безразмерная скорость передвижения границы фазового перехода для процесса конвекции:
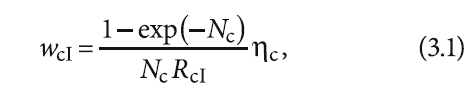
и теплопроводности:
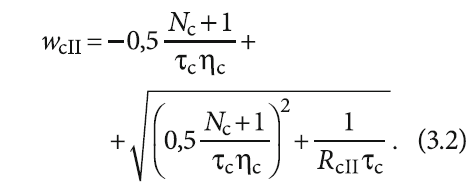
Безразмерное время процесса τc зависит в том числе и от теплофизических свойств ТАМ:
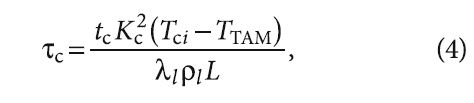
где tc — размерное время протекания процесса; λl, ρl и L — теплопроводность, плотность и скрытая удельная теплота плавления теплоаккумулирующего материала, соответственно.
Коэффициент формы ячейки Rc учитывает соотношение начальной и конечной площадей границы фазового перехода и зависит от безразмерного времени τc:
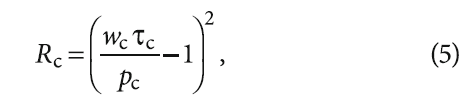
причём комплекс pc зависит от начального диаметра границы фазового перехода dc1 и отношения коэффициента теплопередачи Kc к коэффициенту теплопроводности расплава:

Тогда зависимость безразмерной скорости передвижения границы фазового перехода для сферической ячейки при конвекции:
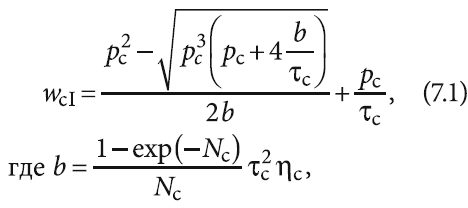
и теплопроводности:
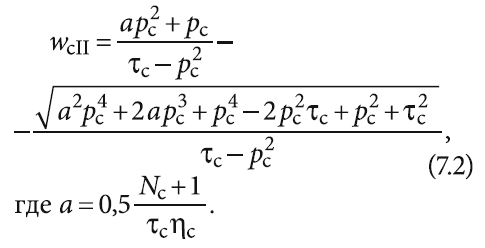
Затем определим температуру стенки ячейки с теплоаккумулирующим материалом:
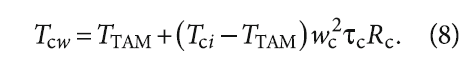
Эффективность процесса заряда оценивается эксергетическим коэффициентом полезного действия:
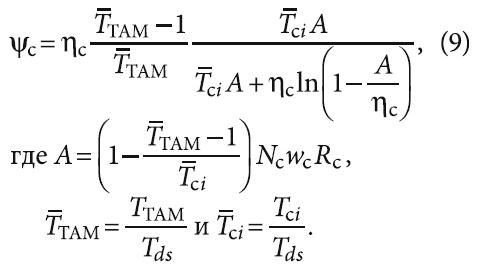
Теперь задаёмся значениями числа теплопередачи Kc, площади поверхности теплообмена F(r1), секундного массового расхода обтекающего ячейку потока mc и его удельной теплоёмкости cp.
По формуле (2) рассчитываем безразмерное число теплопередачи.
Далее, используя теплофизические свойства расплавленного ТАМ (температуру плавления TТАМ, теплопроводность λl, плотность ρl и скрытую удельную теплоту фазового перехода L), число теплопередачи Kc, время заряда tc и температуру потока перед капсулой Tci, вычисляем по формуле (4) безразмерное время процесса.
По предлагаемым зависимостям (7.1) и (7.2) находим значения безразмерной скорости передвижения границы фазового перехода при конвекции wc1 и теплопроводности wc2.
Следует отметить, что, если определяющим механизмом переноса теплоты в капсуле является конвекция, то, подставив формулу (3.1) в формулу (1), получим зависимость:
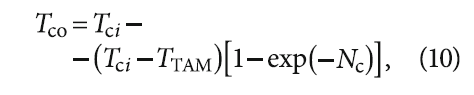
из которой видно, что Tсo не зависит от формы капсулы и безразмерной скорости границы фазового перехода, что совпадает с результатами работы [4].
Выражения (7.1) и (7.2) потребуются для определения температуры стенки капсулы и эксергетического коэффициента полезного действия.
Пример
Оценим влияние безразмерных числа теплопередачи Nc, времени τc на безразмерную скорость передвижения границы фазового перехода в ТАМ при конвекции и теплопроводности, а также на температуру обтекающего потока теплоносителя за сферической капсулой (рис. 1).

Зададим исходные данные, представленные в табл. 1 и 2.
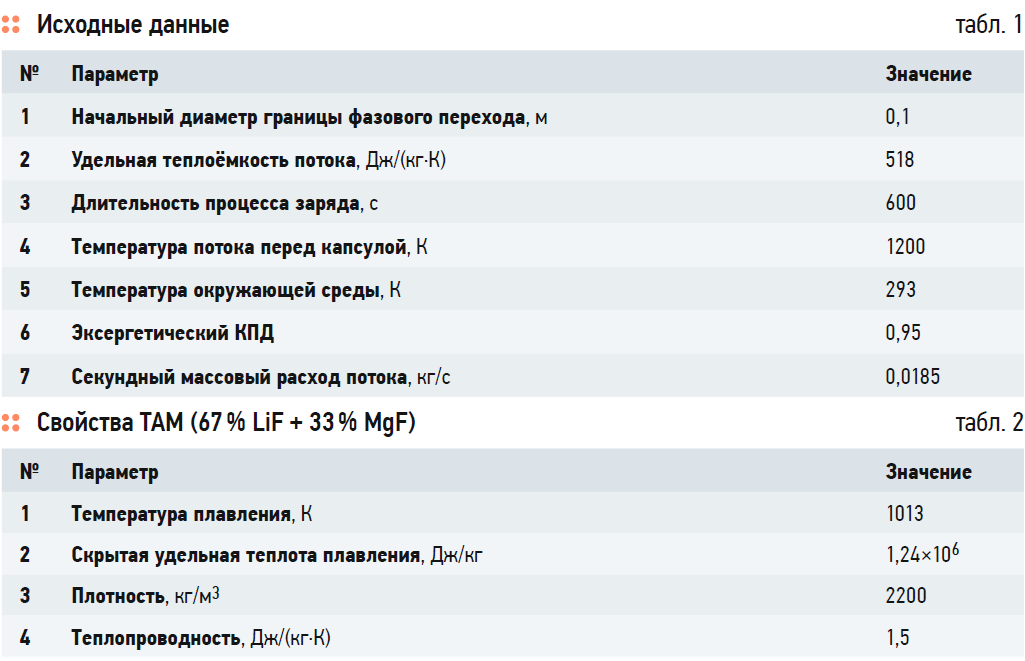
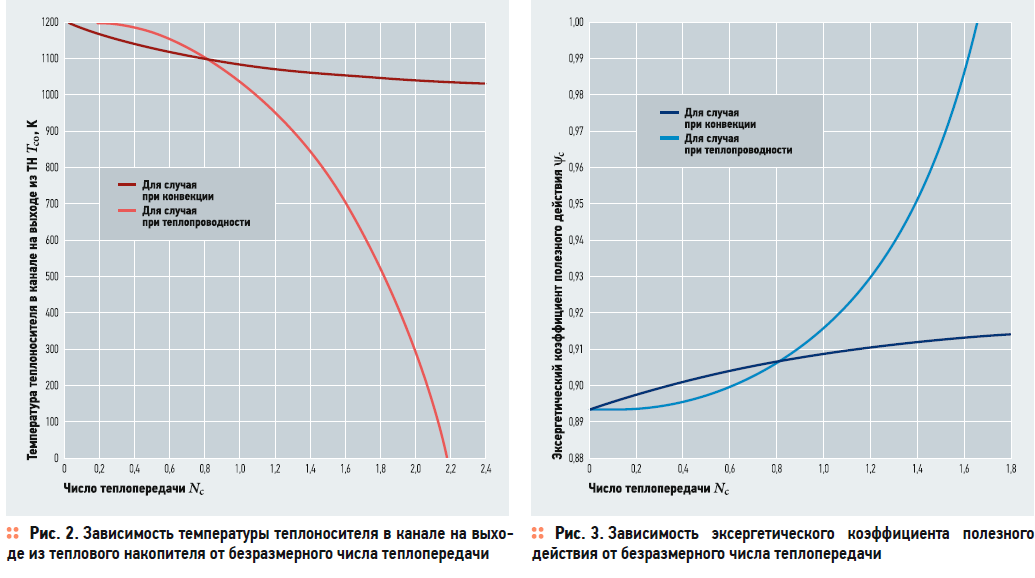
Будем рассматривать изменение безразмерного числа теплопередачи Nc в диапазоне от 0,01 до 3,0. Результаты расчёта по формулам (8) и (9) приведены на рис. 2 и 3.
Термодинамическая эффективность процесса заряда оценивается с помощью эксергетического КПД по формуле (9).
Заключение
Диапазоны величин, приведённых на рис. 2 и 3, связаны с ограниченным количеством теплоаккумулирующего материала. Как при конвекции, так и при теплопроводности наступает момент полного расплавления материала в капсуле. Однако, как это наглядно видно из характера кривых, при конвекции этот процесс происходит быстрее.
Анализ приведённых на рис. 2 и 3 зависимостей показывает, что увеличение безразмерного числа теплопередачи приводит к возрастанию безразмерного времени процесса, при этом безразмерная скорость передвижения границы фазового перехода при конвекции снижается, а при теплопроводности — возрастает.
Тем не менее, это не является противоречием. Так, увеличение Nc приводит к уменьшению температуры теплоносителя Tco за сферой в обоих случаях, и термодинамическая эффективность процесса заряда возрастает.

























