Использование ультразвуковых колебаний в процессах очистки воды от минерально-липидных соединений является частью научной проблемы использования физических методов, которые включают: ультразвуковой, магнитный, высокочастотный, рентгеновский и ультрафиолетовый [1]. Во многих отраслях народного хозяйства — металлургии, машиностроении, теплоэнергетики, тяжёлой промышленности, химических производств и медицине, — использование ультразвукового поля находит широкое применение. Многообразием физико-химических явлений, возникающих в ультразвуковом поле, объясняется применение ультразвука в различных технологиях [1, 2].
Ультразвуковые колебания вызывают диспергирование и эмульгирование веществ, способствуют коагуляции и дегазации, оказывают влияние на процессы кристаллизации и растворения. Ультразвук вызывает разнообразные химические превращения вещества, в числе которых можно назвать реакции окисления, восстановления и полимеризации [2].
В этих условиях постановка вопроса о возможности применения ультразвука для извлечения липидных соединений является актуальной. Однако теоретическая сторона этого вопроса представляет собой научный интерес.
Ультразвуковые колебания относят к упругим колебаниям. При большой интенсивности ультразвуковые волны описываются законами нелинейной акустики. При распространении ультразвуковых волн в жидкости возникают акустические течения, уплотнение и разряжение среды.
К числу нелинейных явлений, возникающих в ультразвуковом поле, относят акустическую кавитацию. В жидкостях ультразвук распространяется в виде объёмных волн [3].
Скорость в среде упругой волны зависит от плотности среды ρ и адиабатического коэффициента сжимаемости βад и вычисляется по следующей формуле:

где с — скорость звука, м/с; ρ — плотности среды, кг/м³; βад — адиабатический коэффициент сжимаемости, Па-1.
Распространение упругих волн в различных средах описывается уравнением:
y = Asin(ω)t, (2)
где A — амплитуда колебаний, мм; ω — циклическая частота, рад/с; t — временной период, с-1.
Звуковая волна, проходя через жидкость, создаёт зоны сжатия и разряжения, меняющиеся местами в каждый полупериод прохождения волны.
При этом возникает знакопеременное давление p [Па], которое можно определить по формуле:
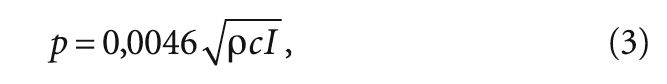
где I — интенсивность звука, Вт/м².
В данной точке среды в течение периода давление p меняется от максимума до нуля, затем снова возрастает до максимального значения и соответствует описанию гармонических колебаний:
p = pmaxsin(ω)t, (4)
где pmax — максимальное звуковое давление (амплитуда давления) [Па]:
pmax = ωcρA. (5)
Теплопроводность и волновое сопротивление среды способствуют поглощению акустической энергии и зависит от плотности среды ρ и скорости звука c. Значение волнового сопротивления среды определяется отношением звукового давления в бегущей плоской волне к колебательной скорости частиц среды:
p/υ = ρc, (6)
где υ — колебательная скорость, м/с.
Частицы упругой среды, в которой распространяются ультразвуковые волны, совершают колебательные движения и поэтому обладают кинетической и потенциальной энергией. Количество энергии, переносимое звуковыми колебаниями за 1 с через площадь в 1 см², которая перпендикулярна направлению их распространения, характеризует интенсивность звука и определяется по формуле:
I = E1c, (7)
где Е1 — плотность энергии, Дж/м³.
Плотность звуковой энергии в каждой точке меняется со временем. Среднее значение плотности энергии в данной точке определяется по формуле:
Е1 = 0,5A2ω2ρ. (8)
Преобразуя уравнения (7) и (8), получим выражение (9):
I = 0,5A2ω2ρc. (9)
При распространении звуковых волн в жидкостной среде интенсивность звука I уменьшается с увеличением расстояния от источника излучения по уравнению:
I = I0e(-2αX), (10)
где I0 — интенсивность звука при X = 0; α — коэффициент поглощения, с²/м.
Важнейшим нелинейным эффектом в ультразвуковом поле является кавитация — возникновение в жидкости массы пульсирующих пузырьков, заполненных паром, газом или их смесью [1, 4].
Сложное движение пузырьков, их захлопывание, слияние друг с другом и т. д. порождают в жидкости импульсы сжатия (микроударные волны) и микропотоки, вызывают локальное нагревание среды, ионизацию. Эти эффекты оказывают влияние на вещество: происходит разрушение находящихся в жидкости твёрдых частиц (кавитационная эрозия), возникает перемешивание жидкости, инициируются или ускоряются различные физические и химические процессы.
Для того чтобы математически описать процесс, происходящий в минерально-липидных соединениях при наложении ультразвукового поля, предположим, что частицы минерального и липидного происхождения представляют собой шарообразную форму, которые под воздействием кавитации будут распадаться на более мелкие части. Причём частицы липидного происхождения в результате освобождения от частиц неорганического состава, стремятся к слипанию между собой. Учитывая плотность воды и частиц, необходимо отметить, что частицы минерального состава всегда тяжелее воды, и поэтому с ними происходит процесс седиментации. Частицы липидного происхождения всегда легче воды, поэтому происходит процесс флотации [5].
Ультразвуковые колебания в кавитационном режиме освобождают частицу липидов от минеральной основы, разрушая вокруг неё плёнку, способствуя выделению липидов из воды, а частицы минеральной основы подвергаются ускоренной седиментации. Минерально-липидные соединения присутствуют в составе шерстомойных сточных вод. Модель минерально-липидного соединения исходной воды показана на рис. 1.
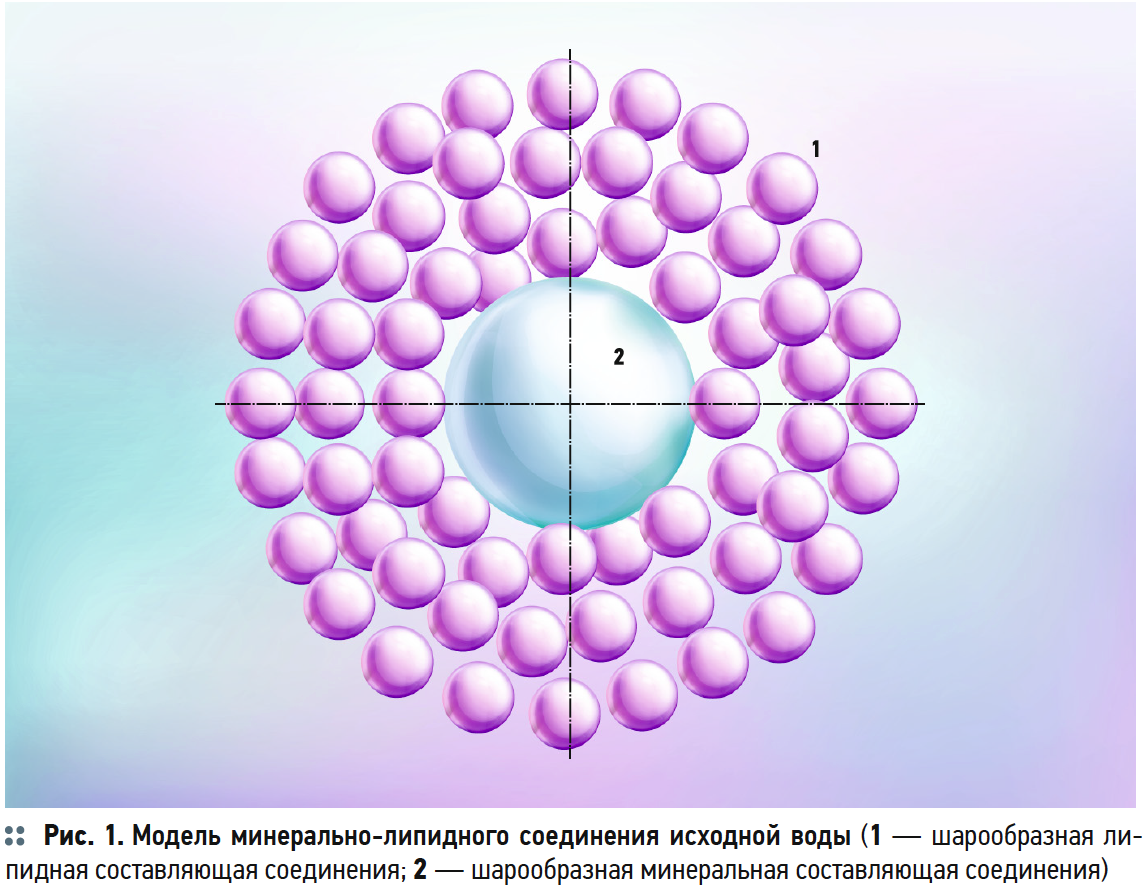
Допускаем, что минерально-липидные соединения имеют форму шара, и их количество в единице объёма составляет n1, при этом диаметр этих частиц будет d1. Рассмотрим процесс воздействия ультразвука на минерально-липидные соединения, по стадиям применительно к единице объёма сточной воды V (рис. 2).
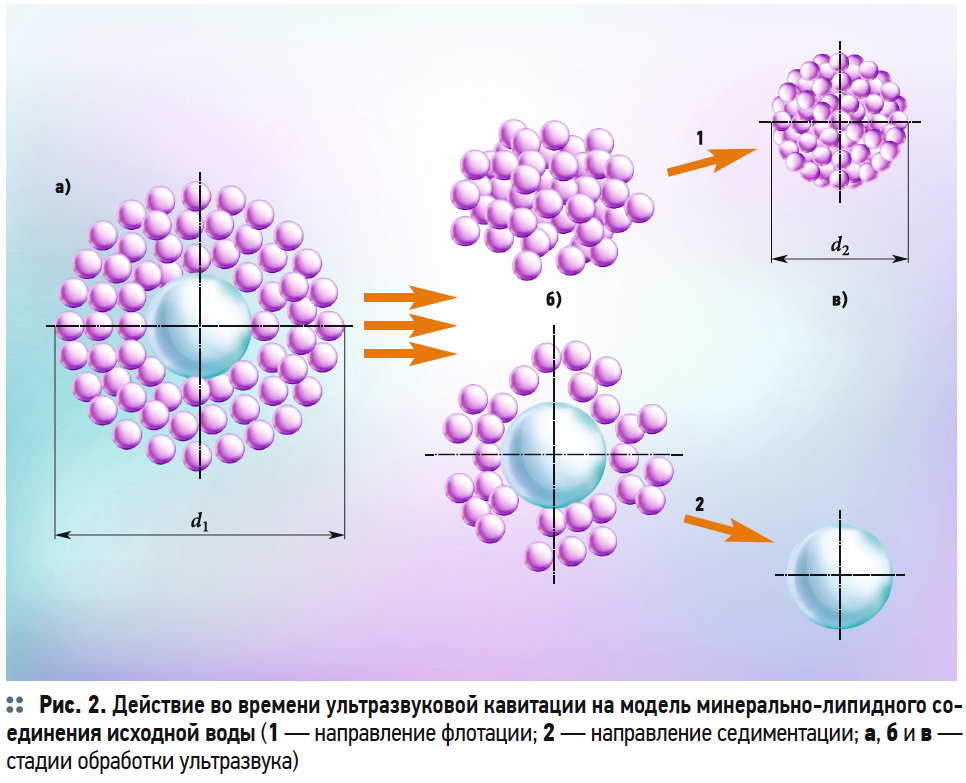
В результате воздействия явления акустической кавитации на частицу диаметром d1 происходит разрушение оболочки липидного происхождения. Частицы липидов диаметром d2 всплывают в воде, а частицы минерального происхождения выпадают в осадок, при этом их диаметр составляет (d1 — d2) [22]. Если число частиц минерально-липидных соединений в единице объёма сточной воды равно n1, то их объём составляет:

где V1 — общий объём минерально-липидных соединений в начальный момент разделения, м³.
Под воздействием акустической кавитации освобождаются все липидные частицы, и их число составляет n2, тогда объём отделённых липидных частиц:

где V2 — общий объём всплывших липидных частиц, м³. Общий объём минеральных частиц диаметром (d1 — d2), выпавших в осадок, будет:
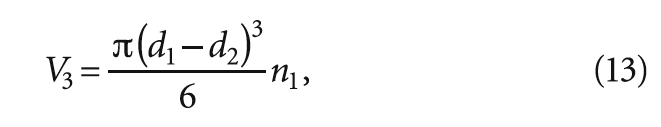
где V3 — общий объём минеральных частиц диаметром (d1 — d2), м³.
Составив уравнение материального баланса, учитывая приведённые выше допущения и уравнения (11, 12, 13), получим следующую сумму
V1 = V2 + V3, (14)
и тогда
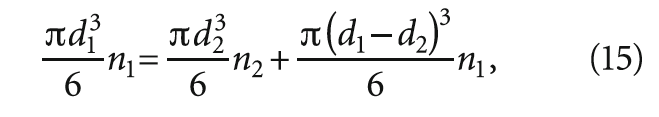
Так как расчёты приведены к единице объёма, составим следующее уравнение:
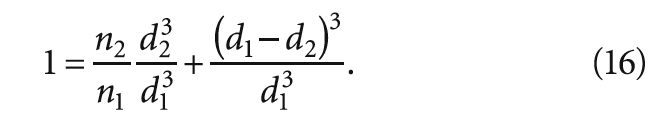
Далее обозначим через N концентрацию липидных частиц в единице объёма, а через ΔN — концентрацию липидных частиц, выделяемых из единицы объёма сточной воды. Составляем пропорцию:
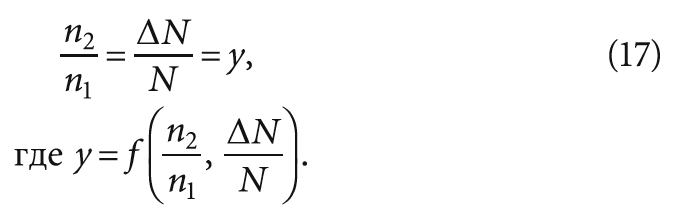
Подставим выражение (17) в уравнение (16) и запишем:
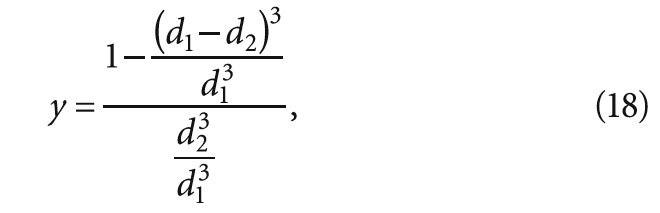
раскрывая скобки, получим выражение:
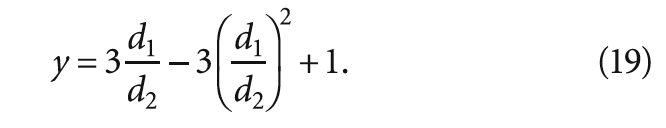
В общем виде это уравнение можно записать как:
y = bx — ax2 + 1, (20)
где a и b — константы, определяемые из эксперимента для каждого конкретного случая.
Выводы
1. Разработана модель ультразвукового воздействия на минерально-липидные соединения в воде.
2. Получена квадратичная зависимость влияния ультразвукового поля на процессы седиментации и флотации минерально-липидных соединений в воде.
























