
Одним из перспективных направлений совершенствования водяных систем солнечного теплоснабжения в странах, характеризующихся отрицательными значениями температуры наружного воздуха зимой и высокими положительными летом, является применение в них самодренируемых гелиоустановок (СДГ) с опорожнением солнечных коллекторов (СК) при остановке циркуляционных насосов [1, 2]. Данное техническое решение позволяет избежать механической поломки СК в зимний период года из-за замерзания в нём воды ночью при отсутствии солнечной радиации, а в летний период года — к её вскипанию и повышению давления водяных паров выше допустимых значений днём при аварийной остановке циркуляционных насосов. Благодаря своей простоте и многочисленным преимуществам по сравнению с другими типами солнечных водонагревателей СДГ нашли широкое применение на практике [3, 5–8].
Штатный режим работы СДГ связан с приходом солнечной радиации и предусматривает ежедневный пуск и остановку циркуляционных насосов гелиоконтура в утренние и вечерние часы. Каждое такое заполнение и дренирование СК может сопровождаться гидравлическими ударами (ГУ) в трубопроводах гелиоконтура вследствие резкого изменения скорости движения теплоносителя [2, 3].
Широко известные в технике традиционные способы защиты от гидроударов, применяемые, например, в системах водоснабжения [4, 9–12], основанные на гашении ГУ, рассчитаны на сравнительно редкие случаи аварийной остановки и запуска насосов при отключении подачи электроэнергии и не являются энергоэффективными решениями для СДГ с ежедневным штатным пуском и остановкой насосов. Поэтому для СДГ известны также оригинальные технические решения [2], исключающие ГУ за счёт применения специальных клапанов с электроприводом. Однако работоспособность таких систем зависит от надёжности электроснабжения и не обеспечивает защиту от ГУ при его внезапном отключении.

Гидравлическим ударом называется внезапное повышение или снижение давления жидкости внутри трубопровода, вызванное любым резким изменением скорости её течения.
Гидравлические удары возникают при пуске и остановке насосов при открытой задвижке на напорной линии, а также при быстром открытии или закрытии регулирующих органов на водоводах и от других причин. Применительно к СДГ при пуске и остановке циркуляционных насосов ГУ можно охарактеризовать как трансформацию кинетической энергии жидкости ρv2/2 в потенциальную энергию, то есть в давление p. Во время такой трансформации могут образовываться ударные волны, которые, проходя по трубопроводу, способны повредить участок трубы далеко от источника их возникновения.
Таким образом, штатный режим работы СДГ, предусматривающий ежедневный пуск и остановку циркуляционных насосов, уже сам по себе связан с трансформацией кинетической энергии жидкости в потенциальную. Поэтому гидроудары в такой системе являются неизбежным следствием самого штатного режима работы СДГ.

Рассмотрим, в каких пределах может изменяться максимальное значение скорости движения теплоносителя в трубопроводах при дренировании СДГ и запуске в работу его насоса.
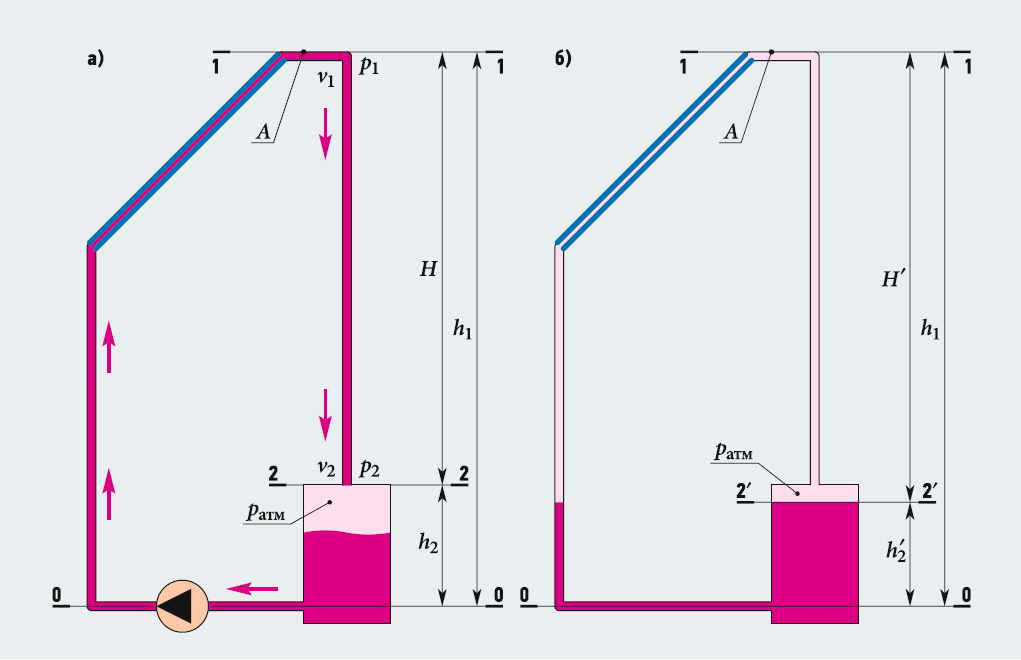
Рис. 1. Принципиальная расчётная схема самодренируемой гелиоустановки (СДГ) при работающем (а) и остановленном (б) циркуляционном насосе
Работа СДГ для стационарного режима (рис. 1а) описывается широко известным уравнением Бернулли:
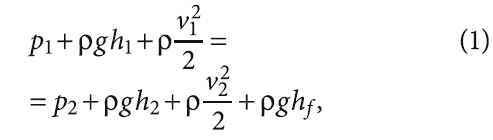
где р1 — статическое давление в верхней части гелиоустановки в сечении 1–1 (рис. 1а), Па; р2 — статическое давление в нижней части гелиоустановки в сечении 2–2, Па; ρ — плотность теплоносителя, кг/м³; g — ускорение свободного падения, м/с2; h1 и h2 — высота столба теплоносителя относительно плоскости сравнения 0–0 в верхней и в нижней частях СДГ, соответственно, м; v1 и v2 — скорости движения теплоносителя в сечениях 1–1 и 2–2, м/с; ρgh1 и ρgh2 — статические давления теплоносителя в сечениях 1–1 и 2–2, Па; ρv12/2 и ρv22/2 — гидродинамические давления теплоносителя в сечениях 1–1 и 2–2, Па; ρghf — потери статического давления теплоносителя на пути от сечения 1–1 до сечения 2–2, Па.
При равенстве поперечных сечений циркуляционных трубопроводов в верхней и в нижней частях СДГ в 1–1 и 2–2, то есть когда v1 = v2, выражение (1) упрощается, и разность статических давлений p2 и p1 между нижней и верхней частями гелиоконтура будет равна:
p2 — p1 = ρgH — ρghf, (2)
где H = h1 — h2 — геометрическая высота дренируемых участков СДГ, м.
Выражая в уравнении (2) разность статических давлений p2 — p1 и потери статического давления ρghf через гидродинамическое давление:
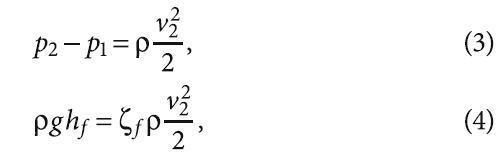
имеем
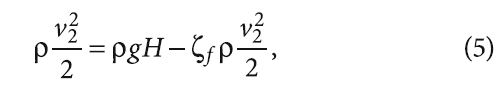
здесь ζf — полный коэффициент сопротивления, учитывающий все потери давления, как по длине последовательно соединённых дренируемых участков трубопровода гелиоконтура, так и в его местных сопротивлениях:
ζf = ζl + ∑ζj, (6)
где ζl — коэффициент сопротивления по длине дренируемых участков трубопровода гелиоконтура:
ζl = λl/D, (7)
где λ — коэффициент трения трубопровода гелиоконтура; D — диаметр трубопровода гелиоконтура, м; l — общая длина дренируемых участков трубопроводов гелиоконтура, м; ∑ζj — сумма коэффициентов местного сопротивления на дренируемых участках гелиоконтура и на входе в дренажный бак.
Решая уравнение (5) относительно скорости истечения v2 при дренировании теплоносителя из гелиоконтуре в дренажный бак, находим:
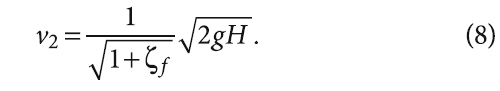
Согласно теореме Н. Е. Жуковского, величина гидравлического удара ∆hуд в напорном трубопроводе связана с изменением скорости движения воды ∆v следующей зависимостью [4, 9]:

где ∆v — положительное или отрицательное приращение (во времени) скорости движения жидкости, м/с; с — скорость распространения упругой деформации жидкости, м/с.
Рассмотрим уравнение (9) применительно к СДГ в режимах пуска и остановки циркуляционного насоса.
Во время пуска циркуляционного насоса СДГ (рис. 1б) начальное движения жидкости отсутствует и увеличение скорости происходит от нуля (уровень воды 2′-2′) до v2 (заполнение системы до уровня 1–1), то есть приращение скорости ∆v = v2 (скорость заполнения СДГ водой принята равной скорости её дренирования v2). Поэтому получается отрицательное значение ∆hуд, обусловливающее возникновение волны понижения давления:

а полный напор во время пуска циркуляционного насоса самодренируемой гелиоустановки, возникающий в трубопроводе при гидроударе, будет равен:
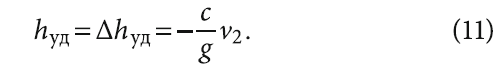
При остановке циркуляционного насоса установившееся движение жидкости в СДГ осуществляется со скоростью v2, которая затем уменьшается до нуля, то есть приращение скорости ∆v = -v2. Поэтому получается положительное значение ∆hуд, обусловливающее возникновение волны повышенного давления:

а полный напор во время остановки циркуляционного насоса СДГ, возникающий в трубопроводе при гидравлическом ударе, будет равен:
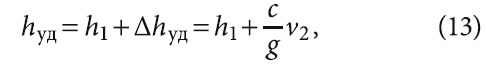
где h1 — напор в СДГ при установившемся течении воды, м.
Для случая круглого трубопровода скорость с распространения упругой деформации жидкости равна [9]:
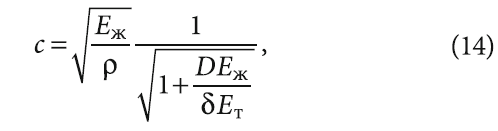
где Eж — модуль объёмной упругости жидкости, Па; Eт — модуль упругости материала стенок трубопровода, Па; δ — толщина стенок трубопровода, м.
Для воды как теплоносителя формула (14) имеет вид [9–10]:
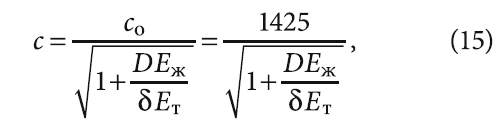
где co — скорость распространения звука в покоящейся жидкости, причём для воды эта скорость составляет
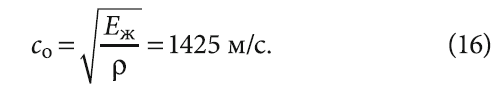
Зависимость между скоростью ударной волны с, её длиной L и временем распространения τф выражается следующей формулой [9–10]:
c = 2L/τф. (17)
В зависимости от времени распространения ударной волны τф и времени продолжительности разгона (или торможения) циркуляционного насоса СДГ при его пуске (или остановке) τз, в результате которого возник ГУ, можно выделить два вида ударов:
- полный (прямой) гидроудар при τз ≤ τф, то есть отражённая отрицательная волна не успевает подойти к насосу до момента его полного запуска (остановки);
- неполный (непрямой) гидроудар при τз > τф, то есть отражённая отрицательная волна успевает подойти к насосу до момента его полного запуска (остановки).
Здесь τз — время закрытия запорного органа (задвижки, вентиля, затвора и т. п.) или пуска и остановки насоса, с; τф — время, в течение которого волна возмущения возвращается к источнику возмущения в виде обратной волны, называемое фазой удара, с.
Отсюда, с учётом формул (17) и (15), можно записать следующие условия для возникновения гидроудара при пуске (остановке) циркуляционного насоса самодренируемой гелиоустановки:
- для полного гидроудара
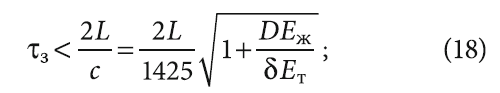
- для неполного гидроудара
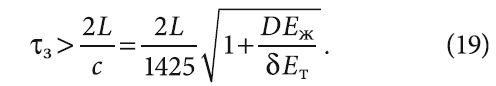
Решая совместно уравнения (12) и (17) с учётом условий (18) и (19), получаем формулу для определения величины ГУ в СДГ в зависимости от его геометрических и режимных параметров и характеристик циркуляционного насоса:

Из формулы (20) следует, при одном и том же диаметре трубопровода СДГ гидравлический удар при пуске (остановке) насоса будет тем сильнее, чем больше длина трубопровода L, чем выше скорость движения воды v2 и чем быстрее разгоняется (тормозится) насос, время τф.
Очевидно, что полный гидравлический удар сильнее неполного. Чем больше время τф, тем вероятнее возникнет более слабый неполный ГУ.
В нашем случае происходит не закрытие запорного органа, а включение (или остановка) насоса, поэтому правомерно считать величину τф равной времени разгона (торможения) насосного агрегата τа, определяемого по формуле [10]:

здесь GD2 — маховый момент насосного агрегата, принимаемый обычно равным маховому моменту электродвигателя [кг· м²], который определяется как:
GD2 = 4gJ, (22)
где J — момент инерции ротора электродвигателя, кг· м²; no — число оборотов электродвигателя в секунду, с-1; Мо — вращающий момент на валу электродвигателя, Н·м.
Особым и наиболее сложным случаем ГУ является удар с разрывом сплошности потока в трубопроводе. Разрыв потока возникает, когда при ГУ дополнительное снижение напора ∆hуд = сv2/g оказывается больше первоначального напора h1 в данной точке трубопровода. При этом давление в трубопроводах падает ниже атмосферного уровня, и поток разрывается — образуются пустоты, заполненные парами воды. При заполнении образовавшихся водо-воздушных полостей происходит соударение противоположных слоёв жидкости, что значительно усиливает гидроудар по сравнению с таковым без разрыва сплошности потока.

Для самодренируемых гелиоустановок данный режим является наиболее характерным при остановке циркуляционного насоса. В работе [2] приведены результаты натурных экспериментальных исследований самодренируемых гелиоустановок с площадью гелиополя солнечных коллекторов 178 м². Отмечено, что через 7–10 с после остановки циркуляционных насосов имеют место отрицательные значения давления до 0,2 бар с гидравлическими ударами.
Критерием возможности нарушения сплошности потока, согласно [10], является соотношение, которое применительно к расчётной схеме самодренируемой гелиоустановки (рис. 2а) имеет вид:
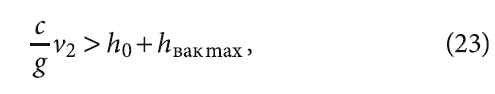
где h0 — гидродинамический напор в трубопроводе, м; hвакmax — величина вакуума, образующегося в наивысшей точке системы под действием атмосферного давления (обычно принимают величину hвакmax = 7–8 м).
В случае разрыва сплошности потока при гидравлическом ударе, возникшем вследствие внезапного отключения насоса, скачок давления составит:
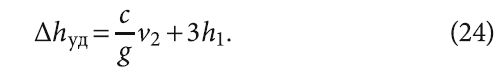
где h1 — статический напор, определяемый как разница между отметкой максимального уровня воды в системе и отметкой установки насоса (рис. 1).
Гидродинамический напор в трубопроводе h0 определяется с учётом скорости течения воды. При остановке потока h0 можно принять равным статическому напору h1.
Если соотношение (23) не выполняется, и разрыва сплошности потока не происходит, то напор при ГУ будет:
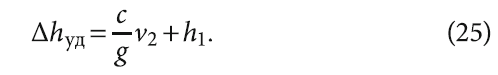
Таким образом, в случае внезапной остановки насоса величина ГУ зависит не только от параметров трубопровода и скорости движения воды, но и от высоты подъёма водяного столба.
Зная высоту Н дренируемых участках СДГ и полный коэффициент сопротивления ζf, который зависит от диаметра D, протяжённости l и материала λ трубопровода, по формуле (8) можно рассчитать величину скорости v2 движения теплоносителя при дренировании или при наполнении системы водой для применяемых на практике гелиоустановок.

В работе [13] представлены характеристики СДГ 16 ведущих мировых производителей. Основные отличия этих гелиоустановок друг от друга состоят в конструкции дренажного бака (отдельный или интегрированный с баком-аккумулятором), протяжённости гелиоконтура L (от 20 до 40 м) и его высоте, то есть разности отметок Н (от 5 до 25 м), площади СК и вида теплоносителя.
Диаметры трубопроводов, их материал, способы соединения с дренажным баком в работе [13] не приведены. Поэтому уравнением (8) целесообразно пользоваться при расчёте конкретных СДГ, когда эти данные закладываются в процессе проектирования установки.

Однако для оценки опасности возникновения ГУ достаточно определить пределы изменения максимального значения скорости движения теплоносителя при дренировании СДГ. При этом, пренебрегая величиной полного коэффициента сопротивления (приняв ζf = 0), то есть считая потери напора по длине и в местных сопротивлениях СДГ равными нулю, из (3) получим:

где vmax — максимальное значение скорости движения теплоносителя при дренировании СДГ, когда отсутствуют потери напора по длине и в местных сопротивления гелиоконтура, м/с.
Так, например, при высоте гелиоустановок Н = 5–25 м [15] максимальная скорость движения теплоносителя при дренировании составит vmax = 9,9–22,2 м/с, что более чем в 10–15 раз превышает допустимую скорость движения воды в системах теплоснабжения vдоп = 1–1,5 м/с [14]. Таким образом, имеется реальная опасность возникновения ГУ при быстром снижении максимальной скорости движения теплоносителя при дренировании с vmax = 9,9–22,2 м/с до нуля.
Разработка «активного» способа защиты СДГ от ГУ при пуске и остановке циркуляционных насосов требует новых подходов и технических методов применительно к самодренируемым гелиоустановкам.
Следует заметить, что общая энергия ГУ в СДГ определяется высотой гелиоустановки Н, то есть вертикальным расстоянием между уровнями, на которых осуществляется заполнение и дренирование системы. Поэтому способы защиты самодренируемых гелиоустановок от повреждения его трубопроводов могут основываться на двух принципиально различных подходах [15]:
- традиционном («пассивный» способ), когда осуществляется гашение общей энергии гидроудара путём увеличения времени процесса, снижения его мощности, максимального давления и максимального усилия, воздействующего на стенки трубы;
- альтернативном («активный» способ), когда осуществляется сохранение общей энергии гидроудара и обеспечивается плавная реверсивная её трансформации с кинетической энергии жидкости в потенциальную энергию и обратно.
Рассмотрим факторы, влияющие на величину гидравлического удара в СДГ при традиционном «пассивном» способе защиты. Эластичные стенки трубопровода значительно снижают величину гидроудара, достаточно легко увеличивая объём трубы или шланга в месте остановки жидкости. Если труба заполнена воздухом, который по мере продвижения жидкости не успевает покинуть трубу с нужной скоростью, это также способно предотвратить сильный гидроудар, поскольку в этом случае воздух играет роль пневматического амортизатора, в котором плавно повышается давление, и потому он оказывает всё большее сопротивление движению жидкости, постепенно замедляя её. Именно эти принципы использует большинство устройств для пассивной защиты трубопроводов от гидроударов.

«Активный» способ защиты СДГ от гидравлического удара предполагает применение в нём активного элемента (АЭ) в виде трубки Вентури (рис. 2), которая обеспечивает как повышение энергетической эффективности системы на 65–80% [16], так и её защиту от ГУ. Это обеспечивается за счёт плавной реверсивной трансформации кинетической энергии гидравлического удара в потенциальную и обратно в АЭ с минимальными гидравлическими потерями [17] (менее 15%).
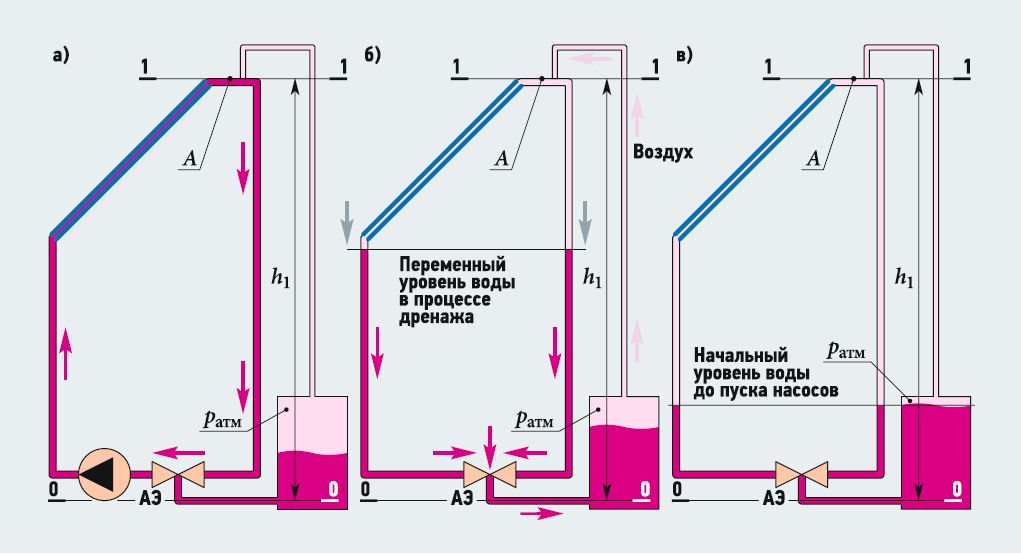
Рис. 2. СДГ с активным элементом (АЭ) [а — стационарный режим циркуляции воды при работающем насосе; б — переходной режим при остановке насоса с плавным переменным уровнем
воды в процессе дренирования; в — начальный режим до запуска насоса в работу]
Применение активного элемента обеспечивает плавное преобразование кинетической энергии жидкости в потенциальную при переходе самодренируемой гелиоустановки из стационарного режима циркуляции воды, при работающем насосе (рис. 2а), в переходной режим при остановке насоса (рис. 2б) или в начальный режим до запуска циркуляционного насоса СДГ в работу (рис. 2в).

Выводы
1. Для борьбы с гидравлическими ударами в СДГ можно выделить два принципиально разных подхода:
- традиционный «пассивный» подход, основанный на гашении общей энергии гидравлического удара, то есть выполнение эластичными стенок трубопроводов, использование пневматических амортизаторов, перфорированных мембран для гашения скорости и т. д.;
- «активный» подход, основанный на плавной реверсивной трансформацией общей энергии гидравлического удара в активном элементе (в трубке Вентури) с переходом кинетической энергии жидкости в потенциальную и обратно.
2. Традиционные способы защиты от гидравлического удара, основанные на его гашении, не являются энергоэффективными решениями для СДГ, так как они не учитывают особенности штатного режима работы СДГ и связаны с большими гидравлическими потерями.
3. «Активные» способы защиты от гидроудара, основанные на применении в СДГ активного элемента в виде трубки Вентури, в которой происходит плавный переход кинетической энергии жидкости в потенциальную и обратно, учитывают особенности штатного режима работы СДГ и обеспечивают наименьшие гидравлические потери.

























