
Введение
Современные технические средства позволяют внедрять сложные системы управления в работу объектов электроэнергетики, решая при этом одну из главных задач — повышение эффективности их работы за счёт сокращения затрат на производство, передачу и потребление электроэнергии. Большое число научных исследований и разработок направлено на достижение указанной цели. Одни решают поставленную задачу за счёт внедрения специализированных технических средств, другие — за счёт использования управляющих мероприятий. Выбор подхода обусловлен специфическими характеристиками объекта, для которого разрабатываются мероприятия.
При создании специализированного программного обеспечения широко используются методы оптимизации, адаптированные под специфические характеристики объекта исследования. В [1] описаны основные методы оптимизации, которые применимы для решения задач в условиях электроэнергетических систем и энергообъединений. Работа [2] посвящена оптимизации электроэнергетической системы по реактивной мощности с использованием метода «роя частиц», что обеспечивает учёт большого числа параметров элементов системы. В [3] авторы рассматривают решение той же задачи, но с применением алгоритма, моделирующего рост нагрузки.
Наряду с известными методами оптимизации, применяемыми для решения задач в энергетике, в связи с развитием современных подходов и технологий разрабатываются новые методики. Так, в [4] впервые приводится алгоритм оптимизации Grey Wolf, позволяющий осуществлять оптимальное управление энергосистем с солнечными электростанциями.
В условиях систем электроснабжения крупных промышленных предприятий одним из мероприятий по повышению эффективности функционирования энергоузла узла является оптимизация режимов работы его источников энергии, заключающаяся в определении оптимальной загрузки генераторов [5] и котлов электростанций [6], экономически выгодном распределении мощности между собственными электростанциями и внешним источником, решении топливной задачи и т. д.

С этой целью разрабатывается и внедряется большое число программных продуктов, позволяющих осуществлять оптимизацию режимов работы электростанций. В [7] авторами предложены положения дифференциально-экзегетического подхода при анализе термодинамических режимов работы установок ТЭЦ, что обеспечивает оптимизацию режима работы электростанции. Авторы работы [8] предлагают использовать алгоритм «хаотической оптимизации» для опреде-ления экономичных режимов работы электростанции. В [9] данная задача решается за счёт применения корреляционного анализа.
Разрабатываются мероприятия, направленные на поиск оптимальных режимов работы специфического оборудования электростанций [10], особенностей работы электростанций [11] и экологических условий [12].
Рассматриваются вопросы, связанные с оптимизацией режимов работы электростанций в условиях современного конкурентного рынка [13].
Вопросы оптимизации режимов работы объектов электроэнергетики и, в частности, промышленных систем электроснабжения остаются актуальными и, ввиду постоянного совершенствования технических и информационных средств, требуют всё новых исследований и разработок. Кроме того, существующие подходы в области оптимизации режимов крупных энергообъектов не решают комплексную задачу определения экономически целесообразных режимов работы при параллельной работе местных электростанций и энергосистемы.
В данной работе предлагается подход, позволяющий смоделировать промышленную систему электроснабжения с собственными электростанциями и узлами примыкания к энергосистеме, с целью определения экономически целесообразного потребления мощности от внешнего источника и выработки электроэнергии местными генерирующими электроустановками.

Теоретическая часть исследования
Оптимизацию режимов промышленных систем электроснабжения, с целью определения оптимального соотношения мощностей между внешними и собственными источниками, предлагается осуществлять с использованием модифицированного метода динамического программирования и последовательного эквивалентирования. Данный подход позволяет задавать исходные данные для расчётов в табличной форме и ограничения в форме равенств и неравенств.
В детерминированной постановке задачу оптимизации формулируется следующим образом — найти минимум целевой функции:
Зn = Σnj=1[Cj(xj) + Cот.j(xj) + C∆Pj(xj) + Cпр.j(xj)] → min, (1)
где xj — оптимальное управление (оптимальная мощность источников энергии) на j-м шаге; Cj(xj) — стоимость расхода пара на выработку электроэнергии при суммарной нагрузке системы электроснабжения Pнагр; Cот.j(xj) — стоимость расхода пара через отборы; C∆Pj(xj) — стоимость потерь активной мощности ∆Pj в системе электроснабжения при заданной нагрузке Рнагр.j(xj); ∆Р — величина потерь активной мощности в сети, МВт; Рнагр.j(xj) — активная нагрузка системы электроснабжения, МВт; Cпр.j(xj) — стоимость приобретаемой электроэнергии Pпр.j при заданной нагрузке Pj(xj); Pпр.j — мощность, приобретаемая из энергосистемы, заданная с использованием технико-экономической модели (ТЭМ) энергосистемы, МВт.
На целевую функцию накладываются независимые ограничения (2):
Pimin ≤ Pi ≤ Pimax,
Pнагр = Σnj=1(Pi) — ∆Р + Σmj=1(Pпр.j),
Pпр.jmin ≤ Pпр.j ≤ Pпр.jmax, (2)
где Pimin и Pimax — минимальная и максимальная величины активной мощности генераторов, соответствующие ТЭМ источников, МВт; n — общее число генераторов в энергоузле; m — число точек примыкания к энергосистеме; Pпр.jmin и Pпр.jmax — минимальная и максимальная величины активной мощности, принимаемой из энергосистемы, МВт.
При этом на целевую функцию накладываются зависимые ограничения в виде допустимых нагрузок на элементах сети и допустимых потерь напряжения:
Uimin ≤ Ui ≤ Uimax, Simin ≤ Si ≤ Simax. (3)
Рекуррентное уравнение, которому должна удовлетворять функция Зn, будет выглядеть следующим образом:
Зn(Pn) = mxn∈inXn{Cn-1[Pn — Pнагр.n(xn)] + Cn(xn) + C∆P(n)(xn) + Cпр.n(xn)}. (4)
Уравнения состояния в результате управления xn будут иметь вид:
Pn = Pn-1 + Pнагр.n(xn) + ∆Pn(xn) + Pпр(n-1). (5)
При решении оптимизационной задачи, как видно из целевой функции (1), учтены потери мощности в распределительных сетях. Для этого разработан алгоритм, более подробно описанный в [14].

Для решения оптимизационной задачи с использованием метода динамического программирования разработана технико-экономическая модель источников электроэнергии промышленной системы электроснабжения (табл. 1). Данная модель представляет собой зависимость суммарной мощности нагрузки энергоузла Pнагр от следующих факторов: мощности i-го генератора t-й электростанции; мощности приёма внешнего источника Рпр при их числе m; затрат на выработку, приём и передачу мощности З в рассматриваемом энергоузле.
С целью оценки баланса мощности в энергоузле модель также учитывает потери активной мощности в рассматриваемой системе электроснабжения.
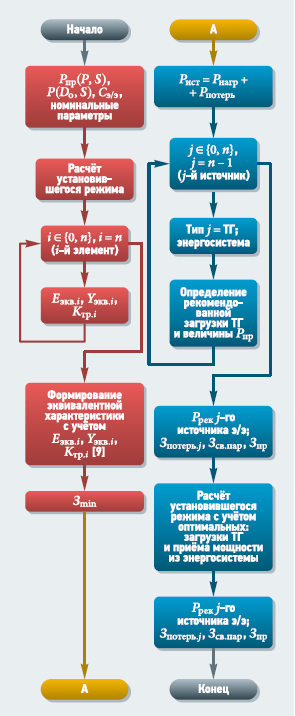
Рис. 1. Алгоритм оптимизации режимов системы электроснабжения с собственными и внешними источниками электроэнергии
Для получения эквивалентной оптимизационной модели энергоузла разработан алгоритм (рис. 1). На основании предложенных подходов разработан программно-вычислительный комплекс (ПВК) КАТРАН-OptActivePower [15], при использовании которого можно осуществлять планирование нормальных, ремонтных и послеаварийных режимов работы источников электрической энергии промышленных энергоузлов.
Практическая часть исследования
Исследования проводились в условиях системы электроснабжения, структурная схема которой приведена на рис. 2. Узел получает питание от трёх собственных крупных электростанций (ТЭЦ, ЦЭС, ПВЭС), а также от трёх внешних источников: ПС «Бекетово», Троицкая ГРЭС, Ириклинская ГРЭС.
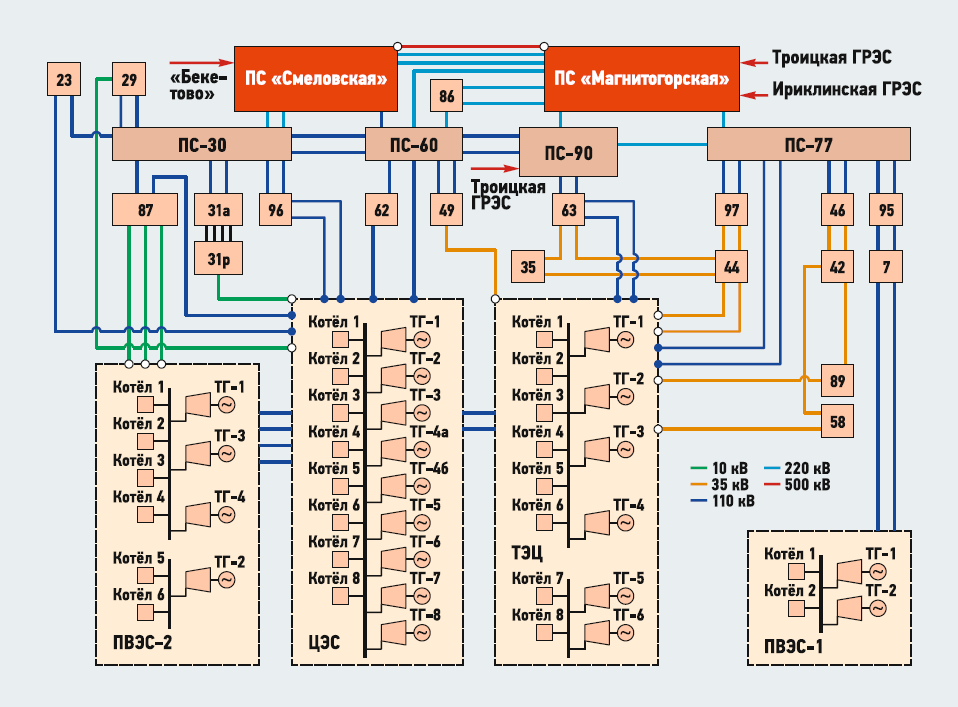
Рис. 2. Структурная схема промышленного энергоузла
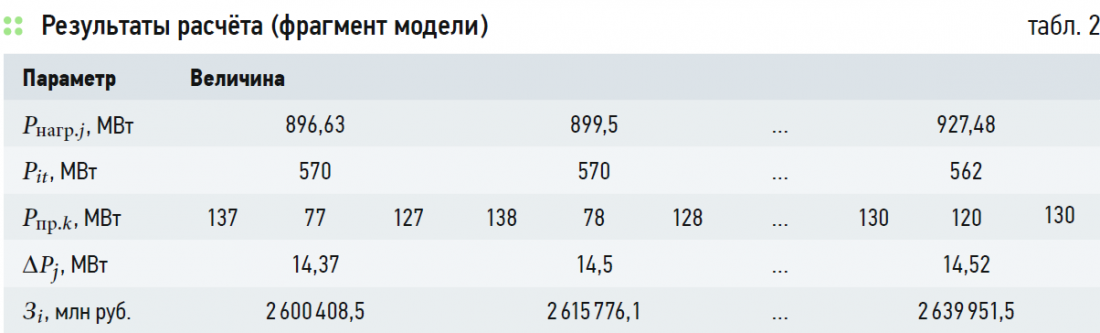
На основании описанного подхода с использованием [15] осуществлён поиск оптимальных режимов работы источников электроэнергии в условиях рассматриваемого объекта. Определены экономически целесообразные величины приёма мощности из энергосистемы, рекомендуемые загрузки генераторов. Фрагмент полученной оптимизационной модели приведён в табл. 2. С целью упрощения представления расчётов в строчке с рекомендуемыми загрузками генераторов собственных электростанций приведена суммарная выработка электростанций рассматриваемого энергоузла.
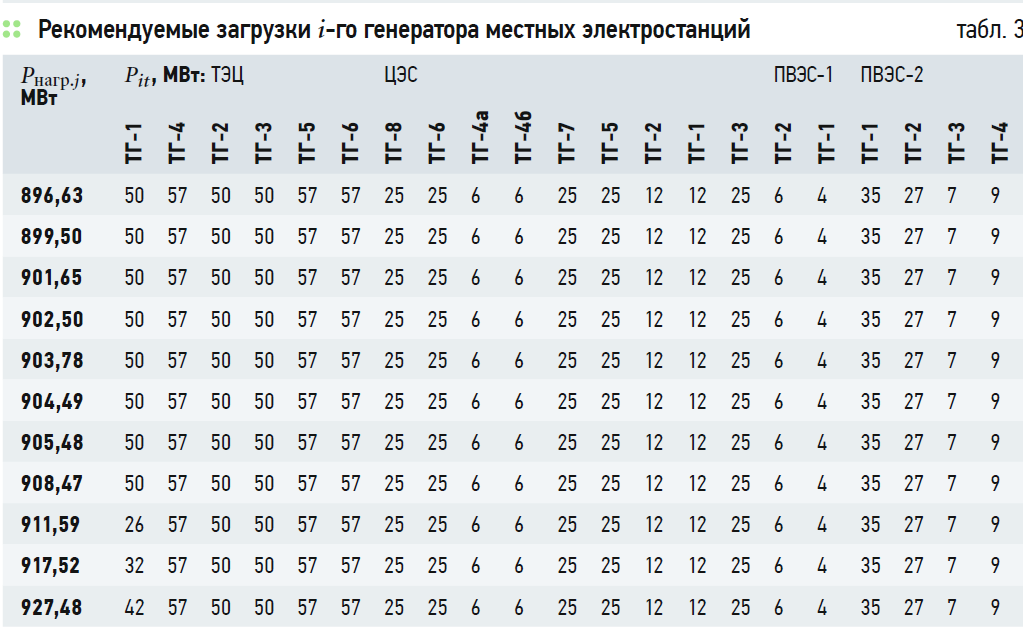
Оптимальные загрузки i-го генератора t-й электростанции подробно приведены в табл. 3.
Кроме того, полученные результаты для всего диапазона нагрузок энергоузла приведены на рис. 3. На данном графике отображена зависимость рекомендуемых загрузок источников энергоузла от возможной мощности нагрузки (при расчётах также учтены потери мощности в балансе, однако на графике они определяются путём расчёта разницы суммарной выработки мощностей источников и мощности нагрузки).
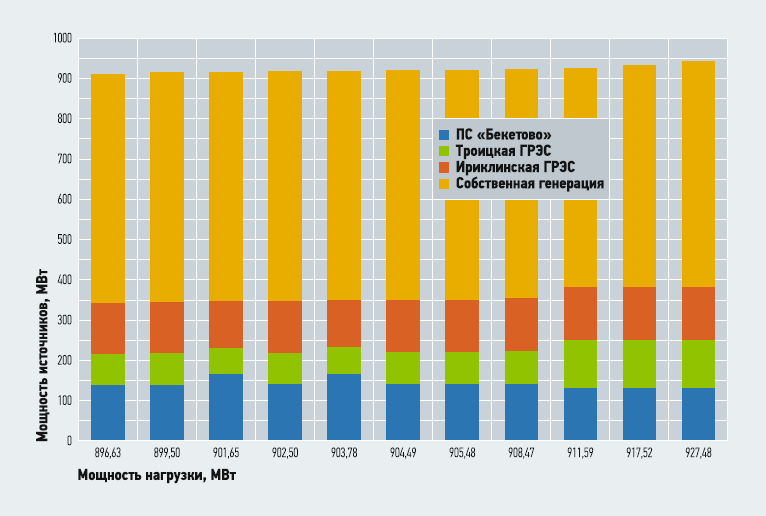
Рис. 3. Зависимость мощности источников электроэнергии от нагрузки
На основании полученных зависимостей можно сделать вывод о том, что большое влияние на изменение мощности, принимаемой из системы, оказывает нагрузка, электрически близкая к ней, что объясняется учётом потерь мощности в распределительных сетях, а следовательно, и их влиянием на баланс мощности в энергоузле.
Заключение
Разработанный подход, реализованный в оригинальном программном продукте, позволяет определить оптимальное соотношение между покупаемой и собственной мощностью промышленного энергоузла. Применение метода динамического программирования обеспечивает поиск оптимальных решений на любом этапе оптимизации и позволяет определить набор экономически целесообразных управлений для всех источников электроэнергии рассматриваемого энергоузла. Подход позволяет прогнозировать нормальные, ремонтные и послеаварийные режимы работы промышленной системы электроснабжения не только с точки зрения надёжности, но и учитывая экономическую составляющую.
Разработанный программный продукт применим для решения задач диспетчерских служб энергохозяйства промышленного предприятия с собственными электростанциями.
























