Для поддержания температуры внутреннего воздуха tв [°C] на требуемом уровне при переменных внутренних и внешних тепловых воздействиях обслуживающие помещение системы обеспечения микроклимата оборудуются системами автоматизации, использующими различные законы регулирования. Разумеется, наиболее предпочтительным и обеспечивающим максимальную точность является непрерывное регулирование, особенно с интегральной составляющей, поскольку при этом статическая ошибка становится равной нулю. Однако для простых агрегатов наподобие индивидуальных сплит-систем до сих пор применяется регулирование двухпозиционного типа, когда устройство попеременно включается и выключается при достижении величиной tв верхнего и нижнего пределов, установленных для данного помещения по требованиям комфортности внутреннего микроклимата. При этом тепло или холодопроизводительность агрегата в течение каждого периода включения оказывается постоянной. Из соображений теплового баланса она, очевидно, определяется значением теплоизбытков и соотношением продолжительности периодов включения и выключения.
Для оценки данной мощности и общего теплового режима помещения, а также условий функционирования климатического оборудования необходимо найти фактическую частоту его переключений. В общем случае для подобных исследований бывает невозможно обойтись без существенного учёта теплообмена на поверхностях ограждений и конвективного переноса теплоты в рассматриваемом объёме, а также нестационарной теплопередачи в массиве строительных конструкций, а также без использования уравнений связи между контролируемой температурой в помещении и тепловым потоком от регулируемых климатических систем. Поэтому решение таких задач чаще всего осуществляется за счёт составления систем дифференциальных и алгебраических уравнений, которые впоследствии приходится решать в основном численными методами, и получаемые в результате зависимости могут оказываться достаточно сложными [1–7].
Тем не менее, в нашем случае можно воспользоваться некоторыми существующими решениями и более простыми приёмами. Обозначим интервал времени до момента включения системы охлаждения или до её последующего выключения как Δτ [с], а допустимый диапазон колебаний tв, при выходе за который происходит срабатывание системы автоматизации, как Δt [К]. Тогда искомую функциональную зависимость для Δτ можно записать таким образом:
Δτ = f(Qпост, Δt, B), (1)
где Qпост — теплоизбытки в помещении [Вт], а параметр B [Вт·с1/2/К], можно вычислить по формуле:
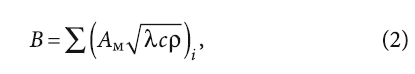
где λ, c и ρ — это, соответственно, теплопроводность [Вт/(м·К)], удельная теплоёмкость [Дж/(кг·К)] и плотность материала [кг/м³] слоя i-го массивного ограждения, обращённого внутрь помещения, например, наружных и внутренних стен и перегородок, а также междуэтажных перекрытий; Aм — площадь каждой из перечисленных ограждающих конструкций, м².
Общий вид зависимости (1) можно установить, в частности, методом размерностей. Если предположить, что Δτ = QaпостΔtbBc, получаем [с] = [Вт]a[К]b[Вт·с1/2/К]c, откуда, очевидно, c = 2, a = -c = −2, b = c = 2, и тогда получаем:
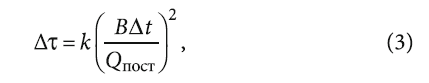
где k — некоторый безразмерный числовой коэффициент.
В то же время для избыточной температуры θв = tв — tв. 0, где tв. 0 представляет собой начальное значение tв, при малых промежутках времени τ [с] с момента появления теплового возмущения можно записать асимптотическое решение [8]:

Заметим, что формула (4), несмотря на её относительную простоту и неучёт ряда других параметров, влияющих на процесс нагрева и охлаждения помещения, например, наличие «лёгких» (безынерционных) конструкций типа окон, вентиляционного воздухообмена и других, достаточно удачно подтверждается экспериментальными данными, в том числе и работами автора [9].
Тогда, если считать θв = Δt, промежуток времени до включения системы охлаждения из (4) можно выразить следующим образом:
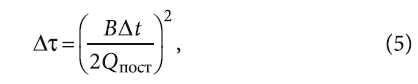
то есть числовой коэффициент k в выражении (2) равен 0,25.
С целью экспериментального подтверждения полученной теоретически величины k были выполнены натурные замеры для тех же условий, в которых проводились исследования, приведённые в [9]. Это необходимо было сделать, поскольку соотношения (4) и, следовательно, (5) всё же были получены при использовании достаточно существенных упрощений и допущений. Как и ранее, для имитации скачка теплопоступлений осуществлялось включение источника конвективной теплоты в виде электрического тепловентилятора, мощность которого составляла в данном случае Qпост = 500 Вт, а величина B была вычислена с использованием реальных теплотехнических показателей материалов ограждающих конструкций здания и размеров помещения. В частности, его площадь была равна 14 м², высота от пола до потолка 3 м, глубина от наружной стены 6 м. Внутренние конструкции выполнены из железобетона плотностью 1200 кг/м³ и общей площадью 64 м², которую необходимо учитывать целиком, так как в условиях данного эксперимента распространение температурной волны в ограждениях будет происходить только в одну сторону, наружная стена из лёгкого бетона плотностью 500 кг/м³ и площадью 7 м² с окном площадью 1,8 м². Тогда значение B оказывается равным около 24 кВт·c1/2/К.
С целью компенсации теплоизбытков применялся внутренний блок сплит-системы, поэтому, что касается диапазона Δt, его естественно принять совпадающим с шагом уровней tв, автоматически поддерживаемых системой регулирования блока, то есть 1 К.
Измеренная величина Δτ при этом составила в среднем около 755 с. Подстановка соответствующих исходных данных в (5) даёт [24000×1/(2×500)]2 = 576 с, что примерно на ¼ ниже экспериментальной, но, с учётом отмеченной грубости первоначальных предположений при выводе (5), данное совпадение можно признать удовлетворительным, так что формула (5) даёт достаточно достоверную оценку Δτ, по крайней мере, по порядку величины.
Заметим, что к рассматриваемому вопросу можно подойти и с использованием теории тепловой устойчивости [10], разработанной для исследования периодических тепловых процессов в помещении и ограждениях, в первую очередь при гармонических колебаниях Qпост и tв. И, хотя в нашем случае изменение теплоизбытков и компенсационного воздействия системы охлаждения происходит скачкообразно, а температура воздуха изменяется в первом приближении пропорционально √τ [см. формулу (4)], в соответствии с [10] при имеющихся допущениях можно записать выражение:

где 0,9 — поправочный коэффициент, учитывающий отставание по фазе изменения tв относительно Qпост; параметры Atв [К] и AQ [Вт] представляют собой амплитуды колебаний tв и Qпост, соответственно; T — период колебаний, с.
Поскольку в рассматриваемом режиме переключение системы охлаждения за время T происходит два раза, очевидно, что Δτ = T/2, а кроме того, по физическому смыслу амплитуды имеем Atв = Δt/2.
В то же время, наоборот, AQ = 2Qпост, потому что для компенсации теплоизбытков в среднем за период необходимо, чтобы во время включения системы её холодильная нагрузка составляла именно 2Qпост, откуда следует, что применение аппарата данной теории также приводит к соотношению типа (3), но с k = π/(4×0,9)2 ≈ 0,24, то есть практически совпадает с (5).
В то же время сопоставление с экспериментальными данными требует некоторой корректировки коэффициента k, который можно принимать в размере около ⅓.
Таким образом, получена зависимость, определяющая частоту переключений системы охлаждения помещения при постоянных теплоизбытках и её двухпозиционном регулировании. Эта зависимость подтверждается сопоставлением различных вариантов аналитического решения, а также экспериментальными данными, имеет достаточно простой вид, требует минимального числа исходных данных и доступна для использования в инженерной практике.

























