Статья ВАК: Моделирование и исследование в программном обеспечении Aspen HYSYS и COMSOL Multiphysics системы отопления путём рекуперации вторичных энергоресурсов

Введение

Непрерывный рост спроса на энергию в стране заставляет постоянно развивать сеть нетрадиционного энергопроизводства: использовать возобновляемые и вторичные источники энергии, а также решать задачи энергосбережения и повышения энергоэффективности топливно-энергетического комплекса, в том числе и за счёт реализации новых проектов малой энергетики для развития бизнеса и бытовой отрасли.

В этом плане мини-ТЭЦ для малого и среднего бизнеса — это эффективный способ снижения затрат предприятий на электроэнергию и отопление и основа повышения производительности в производственной деятельности. Также это реальный высокотехнологичный объект энергетической инфраструктуры быстро развивающихся регионов и новое слово в сфере электротепловых технических решений, работающих как на природном газе, так и на других источниках энергоресурсов, в том числе и на промышленных, сельскохозяйственных и твёрдых бытовых отходах [1].

За последние 15 лет производство установок такого рода в широком диапазоне мощностей выросло почти вдвое, а сама технология локальной выработки электроэнергии и тепла стала настолько совершенной, что себестоимость одного киловатта выработанного электричества оказывается меньше, чем при потреблении его от городских сетей, а тепловая энергия вырабатывается как дополнительный ресурс [2, 3].

Также важно отметить, что мини-ТЭЦ, например, на основе газопоршневой электростанции, двигатель внутреннего сгорания которой вращает вал генератора для выработки электроэнергии, имеет высокую адаптивность к различным режимам и уровням нагрузки. При этом тепловую технологическую энергию работающей ТЭЦ успешно используют для отопления жилья, поскольку современные системы рециркуляции тепловых отходов двигателей позволяют использовать как тепло их выхлопных газов, так и тепловую энергию системы охлаждения механизмов. Необходимо лишь комплектование ТЭЦ водогрейным или паровым утилизационным котлом, либо тепловым насосом (ТН).

Благодаря относительно небольшим размерам и весу для монтажа автономной мини-ТЭЦ требуется лишь подготовленное бетонное основание. В общем случае, как отмечают производители [2, 3], станции работают без капитального ремонта до 30 лет, а с заменой некоторых исполнительных узлов — до 100 лет. Они имеют полностью автоматический режим работы: автоматически регулируется подача топлива и контролируется исправность агрегата в реальном времени. А роль обслуживающего персонала сводится к проведению оперативных переключений, наблюдению и контролю параметров.

Газовые мини-электростанции могут обеспечить электричеством как энергоёмкие предприятия, так и социальные объекты, и небольшие загородные дома. В зависимости от исполнения они гарантируют производство электричества в объёме от 5 кВт до нескольких мегаватт. При этом электростанции работают на любом типе газообразного топлива, в том числе и на биогазе.

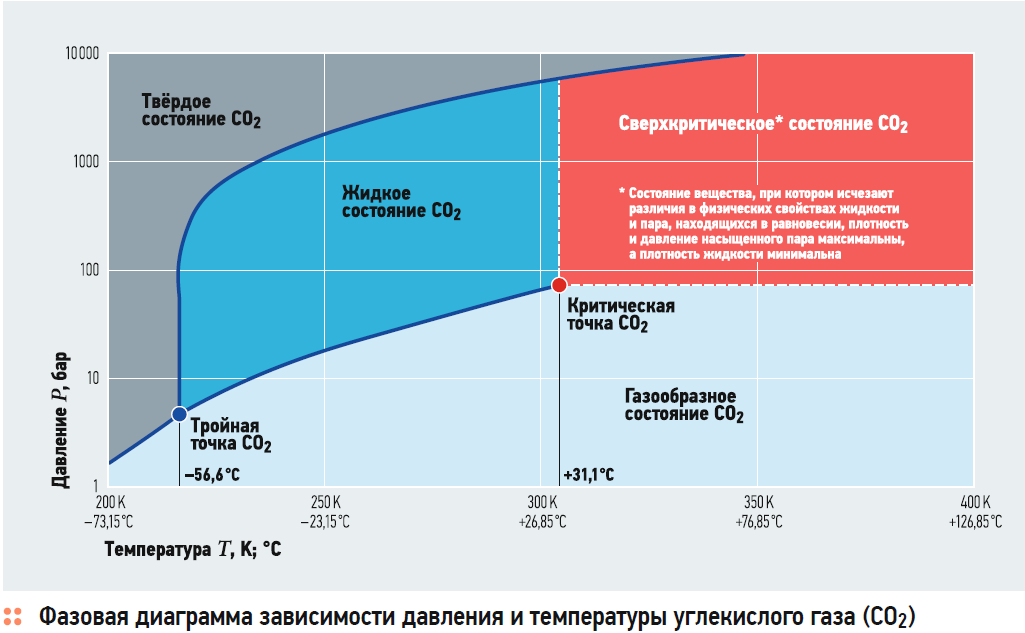
В данной работе решается задача моделирования и исследования системы теплонасосного отопления помещений за счёт рекуперации вторичной энергии двигателя внутреннего сгорания мини-ТЭЦ с помощью ТН. В качестве хладагента рассматривается диоксид углерода (R744 по классификации хладагентов). Такой выбор связан с уникальными термодинамическими и теплофизическими свойствами этого хладагента [4], а также продиктован экологическими требованиями, так как диоксид углерода считается эталонной единицей при расчёте потенциала глобального потепления (Global Warming Potential, GWP = 1) и имеет нулевой потенциал разрушения озонового слоя Земли (Ozone Depletion Potential, ODP = 0). Диоксид углерода нетоксичен и негорюч. Последнее свойство особенно важно для узлов и деталей ТН при высокотемпературных процессах термодинамического цикла, проходящего в транскритической или сверхкритической областях. Именно в сверхкритическом состоянии (sCO₂) этот хладагент обладает большей плотностью и объёмной теплоёмкостью по сравнению с другими рабочими жидкостями, то есть является более энергоёмким.

Подобные задачи для ТН на хладагенте R744, как установки для регенерации отходящего тепла технологических процессов, проектируют и решают в основном по технологиям с газотурбинными расширителями на основе термодинамических циклов Ренкина и Брайтона [5]. Различают открытый цикл, в котором нагрев рабочего вещества происходит прямо в камере сгорания, и замкнутый цикл, в котором нагрев происходит косвенно с помощью теплообменника (или нагревателя). Эти циклы имеют большое количество модификаций различной мощности и эффективности в зависимости от используемых источников тепловой энергии. Однако основные различия между ними связаны с явлением конденсации хладагента.

В цикле Ренкина термодинамический процесс проходит в двух областях: в сверхкритической и докритической. Он является транскритическим, так как содержит переход sCO₂ при охлаждении в конденсаторе из сверхкритического состояния в жидкую фазу. Следующий этап цикла — сжатие жидкого хладагента — происходит с использованием насоса. Это замкнутый цикл, поскольку рабочая жидкость циркулирует в замкнутом контуре и нагревается косвенно с помощью внешнего источника тепла.

В цикле Брайтона термодинамический процесс протекает полностью в сверхкритической области. Превышение критической температуры делает невозможным конденсацию, и она заменяется охлаждением газообразного хладагента в сверхкритическом состоянии. Поэтому вместо конденсатора в цикле Брайтона используется газоохладитель (ГО), в котором не происходит изменения фазового состояния хладагента. На этапе сжатия газообразного sCO₂ применяется компрессор. Цикл Брайтона имеет открытый, замкнутый и полузамкнутый варианты [5, 6].

Указанные различия переходят и на уровень технологических решений, таких как выбор температуры в нагревателе и рабочего давления цикла, определяемого параметрами газотурбинного расширителя и насоса (или компрессора). Поэтому данные технологии ТН на R744 могут эффективно работать в том числе и за счёт тепловой энергии выхлопных газов двигателей внутреннего сгорания различной мощности, например, поршневого двигателя мини-ТЭЦ [6]. В этом случае используется замкнутый цикл Брайтона, в котором нагрев происходит косвенно с помощью теплообменника, аналогично циклу Ренкина.

Для исследования функциональных характеристик ТН, работающего на диоксиде углерода в транскритическом цикле, авторы ранее предложили использовать ПО Aspen HYSYS, позволяющее моделировать рациональные структуры теплотехнического оборудования и оптимизировать его термодинамические циклы, и COMSOL Multiphysics для детального моделирования отдельных узлов [7].

Исследуемая модель и её результаты

В рамках поставленной задачи моделируется работа ТН на диоксиде углерода, как в транскритическом, так и в сверхкритическом цикле. На первом этапе моделирования термодинамического цикла теплонасосной установки (ТНУ) рассматривается технология на основе цикла Ренкина с использованием тепловой энергии выхлопных газов двигателя внутреннего сгорания мини-ТЭЦ малой и средней мощности (температура выхлопных газов 400–450°C). Структурная схема данного термодинамического цикла достаточно проработана исследователями, как за рубежом, так и у нас в стране [5, 6, 8].

Выхлопные газы, несущие сбросовое тепло технологического процесса, непосредственно омывают первичный теплообменник, размещённый на выходе потоков продуктов сгорания и выполненный, например, в виде трубчатого змеевика с потоком жидкого хладагента внутри. Тепло выхлопных газов переводит жидкий хладагент в перегретый пар, который с температурой T1 и давлением P1 поступает в расширитель в виде турбины. Турбина вращает вал генератора, который вырабатывает электроэнергию, как правило, для нужд самой мини-ТЭЦ.

Отработавший после турбины газообразный хладагент поступает в следующие узлы цикла, где продолжает отдавать тепло, в том числе встречному потоку во внутреннем теплообменнике-рекуператоре и отопительной воде в конденсаторе. После фазового превращения жидкий хладагент сжимается и, в конечном итоге, вновь направляется в первичный теплообменник к источнику тепла — выхлопным газам мини-ТЭЦ для повторения термодинамического цикла.

Начальные параметры рассматриваемого цикла: T1 = 300°C, P1 = 31 МПа, тепловая производительность турбины Lтур = 118 кВт, её внутренний относительный КПД равен 82%. Температурный напор на холодном конце рекуператора ∆Tрек = 10 K. Потери тепла в конденсаторе составляют 3 К. Гидравлические потери давления в трубопроводах и узлах цикла условно приняты нулевыми (модель 1).

При моделировании цикла ТН в ПО Aspen HYSYS заданы потоки диоксида углерода с пакетом свойств Пенга — Робинсона и воды с пакетом Уилсона, соответственно. С помощью функций «подбор» фиксировались заданные параметры хладагента в узлах структурной схемы цикла: температура после нагревателя E-101, равная 300°C (ADJ-1); тепловая нагрузка расширителя K-100, равная 118 кВт (ADJ-2); отсутствие паровой фазы CO₂ после охладителя Е-100 (ADJ-3); давление после насоса P-100, равное 31 МПа (ADJ-4). Функция «задать» SET-1 передаёт значение температурного напора из точки 5 на входе в холодную сторону теплообменника LNG-100 в точку 3 на выходе из его горячей стороны. Оптимизация расхода хладагента с помощью встроенной функции «оптимизатор» проводилась при условии максимальности внутреннего КПД цикла, при этом в расчётной схеме с помощью функции ADJ-2 варьировалась мощность расширителя.

На рис. 1 представлены функциональные характеристики ТН на sCO₂ в цикле Ренкина. Пронумерованным состояниям потока хладагента на структурной схеме рис. 1а соответствуют точки термодинамического цикла диаграммы T-s на рис. 1б и диаграммы Р-h на рис. 1в, которые построены в программе Mathcad по методике [8]. Массовый расход хладагента задан в точке 1 и остаётся постоянным на всем протяжении цикла.

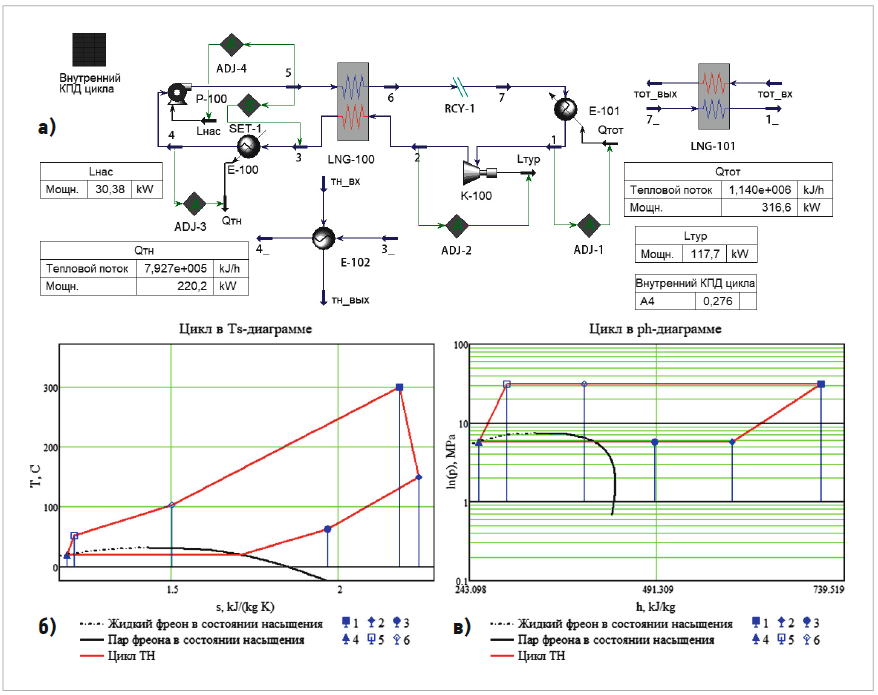
Рис. 1. Функциональные характеристики термодинамического цикла Ренкина теплового насоса на основе сверхкритического диоксида углерода sCO₂ (модель 1) [а — структурная схема; б — диаграмма T-s-цикла; в — диаграмма Р-h-цикла (в логарифмическом масштабе)]

Из начальной точки 1 (T1 = 300°C, P1 = 31 МПа) на выходе из первичного теплообменника-нагревателя E-101 sCO₂ в паровой фазе с высокой энергией поступает на расширение в турбину K-100 и приводит в действие генератор: 1–2 — адиабатное расширение паров в турбине (T2 = 147,7°C, P2 = 5,73 МПа). Затем расширенный sCO₂ охлаждается в рекуперативном теплообменнике LNG-100, где отдаёт тепло встречному потоку хладагента: 2–3 — изобарическое охлаждение (T3 = 61,72°C, P3 = 5,73 МПа). Далее в охладителе Е-100 хладагент передаёт теплоту теплоносителю (отопительной воде) и конденсируется в жидкость: 3–4 — изобарическое охлаждение sCO₂ с транскритическим переходом (рис. 1б и 1в) и конденсацией на линии насыщения в точке 4 (T4 = 20,01°C, P4 = 5,73 МПа). Вслед за этим с помощью насоса Р-100 повышается давление и температура хладагента с переходом в состояние сверхкритической жидкости (рис. 1б и 1в): 4–5 — адиабатное сжатие жидкого sCO₂ (T5 = 51,72°C, P5 = 31 МПа). Затем жидкий sCO₂ закачивается насосом в теплообменник-рекуператор LNG-100, где дополнительно нагревается: 5–6 — изобарический нагрев sCO₂ без изменения агрегатного состояния (T6 = 100,2°C, P6 = 31 МПа). Параметры потока хладагента из точки 6 на выходе из внутреннего теплообменника передаются в цикле в точку 7 на входе в первичный теплообменник. Тепло выхлопных газов нагревает sCO₂ до состояния сверхкритического пара: 7–1 — изобарический нагрев жидкого sCO₂ с условным изменением агрегатного состояния (рис. 1б и 1в). Затем цикл повторяется. Полученные параметры потока хладагента в характерных точках цикла занесены в табл. 1.

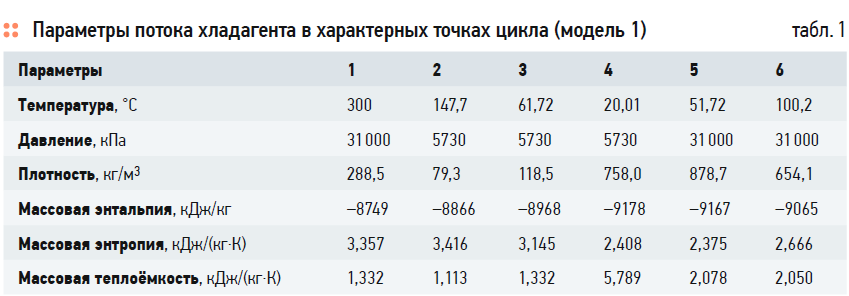
На рис. 1а также отдельно показаны конденсатор как теплообменник E-102 с входным и выходным потоками хладагента sCO₂ и теплоносителя (отопительной воды) и первичный теплообменник LNG-101 с входным и выходным потоками хладагента и теплоотдатчика (выхлопных газов), соответственно. При массовом расходе отопительной воды 4600 кг/ч она нагревается от входной температуры 20°C до выходной температуры 60,85°C. Массовый расход теплоотдатчика составляет 2200 кг/ч при величине входной температуры 400°C.

Оптимизация цикла при массовом расходе хладагента m* = 3600 кг/ч даёт мощность турбины Lтур = 117,7 кВт, мощность насоса Lнас = 30,38 кВт и мощность теплового потока в первичном теплообменнике Qтот = 316,6 кВт. При этом значение внутреннего КПД цикла составит:

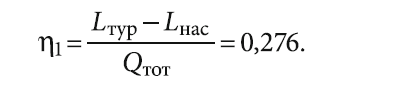
Из табл. 1 видно, что изменения параметров потока CO₂ при переходах между характерными точками цикла соответствуют процессам, описанным выше. Например, кратный рост плотности и теплоёмкости в точке 4 по сравнению с точкой 3 показывает переход sCO₂ из сверхкритического состояния в жидкость, а существенно менее резкое уменьшение этих параметров между точками 6 и 1 — условный переход sCO₂ от сверхкритической жидкости к сверхкритическому пару.

Однако нагрев sCO₂ происходит без затрат энергии на скрытую теплоту фазового перехода, и внутренняя энергия хладагента в сверхкритической области не изменяется скачком. Поэтому изменение характеристик sCO₂ между значениями на входе и на выходе из первичного теплообменника должно происходить равномерно. Это, в свою очередь, гарантирует стабильную работу турбины, генератора и ТНУ в целом. Подтвердить эффективность работы первичного теплообменника можно моделированием протекающих в нём физических процессов. Но расчёт теплообменников в Aspen HYSYS проводится методом логарифмической средней разности температур по алгебраическим формулам [7], что не даёт детальной картины процесса теплообмена, поэтому проведено моделирование и исследование данного узла на основе дифференциальных уравнений в частных производных в ПО COMSOL Multiphysics.

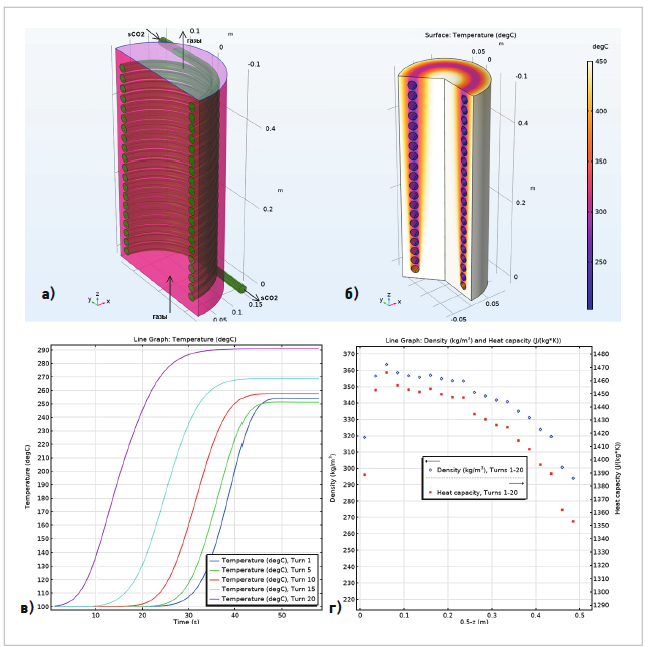
Рис. 2. Геометрия и функциональные характеристики трубчатого змеевикового теплообменника [а — корпус и змеевик с входными и выходными отверстиями (сечение плоскостью yOz); б — стационарное распределение температур хладагента и выхлопных газов в объёме теплообменника; в — изменение средней температуры хладагента в отдельных витках (55 с); г — распределение средних значений плотности и массовой теплоёмкости sCO₂ по всем виткам]

Результаты моделирования представлены на рис. 2. Геометрия теплообменника в виде трубчатого змеевика, размещённого в выхлопной трубе двигателя внутреннего сгорания, показана на рис. 2а сечением корпуса теплообменника плоскостью yOz.

Длина цилиндрической части корпуса — 0,5 м, диаметр — 0,3 м, внутренний и внешний диаметры трубки змеевика — 20 и 25 мм. Трубка изогнута в виде спирали и размещается внутри цилиндрического воздушного канала соосно ему. Количество витков — 20. Видно, что геометрия теплообменника почти осесимметрична. По каналу снизу вверх проходят горячие выхлопные газы, а хладагент sCO₂ прокачивается через змеевик в противоположном направлении. Материал корпуса — конструкционная сталь, трубки — медь.

Заданные размеры элементов теплообменника и найденные ранее массовый расход хладагента 3600 кг/ч и теплоносителя 2200 кг/ч соответствуют турбулентным потокам в корпусе и трубках. Температура sCO₂ на входе 100,2°C, выхлопных газов на входе — 400°C. Стационарное уравнение теплообмена решалось с помощью интерфейсов Turbulent Flow, k-ε и Heat Transfer in Fluids. Однако модель можно упростить, предположив, что и геометрия, и поток газов полностью осесимметричны, и использовать интерфейс 2D axisymmetric с отдельными граничными условиями конвективного теплового потока на внутренних границах каждого витка змеевика [9].

На рис. 2б приведено распределение температур выхлопных газов и хладагента в области теплопередачи, соответствующее стационарному решению, то есть установившимся потокам. Видно, что температура sCO₂ увеличивается по мере прохождения потока хладагента по змеевику: от 253°C в верхнем, первом витке теплообменника до 292°C в нижнем, 20-м витке. Таким образом, расчёт температур в Aspen HYSYS подтверждается с приемлемой степенью точности.

Однако для анализа эффективности теплообменника важно получить более детальное представление о характере изменения температуры хладагента в каждом витке змеевика в зависимости от времени. С этой целью моделировалось начало процесса теплообмена в змеевике на этапе пуска ТН после получения устойчивых параметров хладагента на входе в теплообменник. Время работы до стабильного режима составило около 45 с. На рис. 2в дано изменение средней температуры sCO₂ в первом (синяя линия), 5-м (зелёная линия), 10-м (красная линия), 15-м (голубая линия) и 20-м (фиолетовая линия) витках в течение 55 с. Видно, что температура хладагента в каждом витке увеличивается равномерно: от начальной для всех витков 100,2°C до найденной на этапе стационарного решения для каждого витка. Конечная температура растёт с номером витка, но первый виток выделяется скачком температуры по сравнению с несколькими следующими (не показаны на рис. 2в). Это может объясняться его положением на выходе из воздушного канала и особыми условиями конвекции.

На рис. 2 г. показано распределение средних значений плотности и массовой теплоёмкости sCO₂ по всем виткам для стационарного решения. Видно, что эти величины, связанные обратной зависимостью с ростом температуры, уменьшаются при проходе змеевика, кроме нескольких первых витков. Провал плотности (318 кг/м³) и теплоёмкости [1387 Дж/(кг·К)] на первом витке вызван отмеченным на рис. 2в скачком температуры. На нескольких следующих витках графики выравниваются. В целом изменение параметров sCO₂ по виткам происходит достаточно равномерно с незначительными колебаниями. Конечные значения плотности и массовой теплоёмкости sCO₂ на 20-м витке [294 кг/м³ и 1353 Дж/(кг·К), соответственно] близки к ранее найденным (табл. 1).

Таким образом, результаты моделирования теплообменника в COMSOL Multiphysics близки к ожидаемым, теплообмен проходит достаточно эффективно, что позволяет прогнозировать стабильную работу ТНУ в целом.

Второй этап моделирования термодинамического цикла ТНУ основывается на технологии замкнутого цикла Брайтона, также с использованием тепловой энергии выхлопных газов двигателя внутреннего сгорания, но для мини-ТЭЦ средней и большой мощности (температура выхлопных газов 600–700°C и выше). Варианты структурных схем на основе термодинамического цикла Брайтона широко представлены в зарубежных исследованиях [5, 6, 10]. В то же время, как показал анализ этих исследований, термодинамические циклы на sCO₂ особенно чувствительны к условиям охлаждения в энергетических системах и иногда могут вызывать непрогнозируемые результаты. Это приводит к конструктивной вариации ряда узлов структурой схемы с целью повышения эффективности функционирования термодинамического цикла [11].

Принципиальные различия циклов Ренкина и Брайтона были отмечены выше. В первом случае давление конденсации определяется из условия насыщения. Но в цикле Брайтона конденсации sCO₂ не происходит, и давление хладагента на выходе из ГО не определяется по температуре однозначно. В то же время анализ изменения характеристик sCO₂ при охлаждении позволяет определить так называемую «псевдокритическую» температуру. Она связана с резкими изменениями плотности и теплоёмкости в изобарном процессе вблизи критической точки.

Температура Tpc, при которой удельная теплоёмкость становится максимальной для данного давления, называется «псевдокритической» (pseudo-critical).

Высокая плотность хладагента на входе в компрессор снижает энергопотребление и улучшает общие тепловые характеристики цикла так же, как и высокая теплоёмкость. При охлаждении sCO₂ начальное изменение производительности невелико, но, когда температура достигает Tpc, производительность резко возрастает. Когда же рабочее давление приближается к критическому Pс, пик роста удельной теплоёмкости становится острее, что значительно увеличивает коэффициент теплообмена. Быстрые и нелинейные изменения удельной теплоёмкости sCO₂, в зависимости от температуры и давления, можно оптимизировать, связав Tpc с рабочим давлением по формуле [4, 11]:

Tpc = 122,6–6,124p — 0,1657p2 + 0,01773p2,5–0,0005608p3, (1)

где температура выражена в [°C], давление в барах, и которая справедлива при условии 75 ≤ p ≤ 140.

Начальные параметры цикла: после первичного теплообменника T1 = 500°C, P1 = 23 МПа, давление после турбины P2 = 8 МПа, температура после ГО, найденная по формуле (1), T4 = 34,63°C, температурный напор на холодном конце рекуператора ∆Tрек = 100 K. Потери тепла в ГО составляют 3 К. Гидравлические потери давления в трубопроводах и узлах цикла условно приняты нулевыми (модель 2).

Моделирование цикла Брайтона теплового насоса в ПО Aspen HYSYS выполнялось аналогично моделированию цикла Ренкина. Различия связаны с параметрами цикла: функция «подбор» ADJ-1 задаёт температуру после нагревателя E-101 (500°C); ADJ-2 — давление после расширителя K-100 (8 МПа); ADJ-3 — температуру после охладителя E-100 (34,63°C); ADJ-4 — давление после компрессора K-101 (23 МПа). Функция «задать» SET-1 передаёт значение температурного напора из точки 5 в точку 3.

Оптимизация цикла с целью максимума внутреннего КПД проводилась при условии равенства расхода хладагента и мощности турбины значениям из модели 1: m* = 3600 кг/ч, Lтур = 118 кВт, при этом в расчётной схеме с помощью функции ADJ-2 варьировалось давление после расширителя.

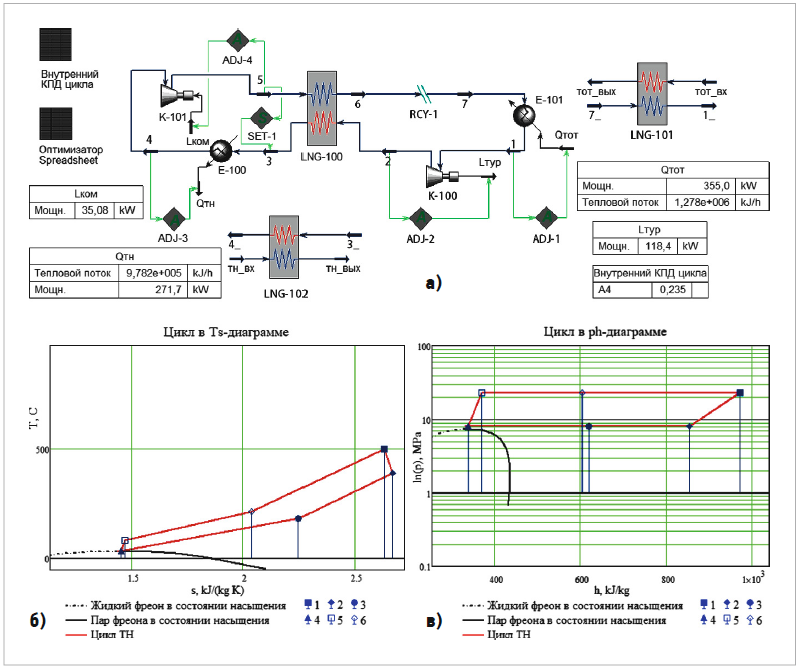
Рис. 3. Функциональные характеристики термодинамического цикла Брайтона ТН на sCO₂ (модель 2) [а — структурная схема; б — диаграмма T-s-цикла; в — диаграмма Р-h-цикла (в логарифмическом масштабе)]

На рис. 3 представлены функциональные характеристики ТН на sCO₂ в цикле Брайтона. Пронумерованным точкам на структурной схеме рис. 3а соответствуют точки термодинамического цикла на диаграммах T-s (рис. 3б) и Р-h (рис. 3в), построенных по методике [8].

Из начальной точки 1 (T1 = 500°C, P1 = 23 МПа) на выходе из первичного теплообменника-нагревателя E-101 sCO₂ поступает в турбину K-100: 1–2 — адиабатное расширение в турбине (T2 = 387,3°C, P2 = 8 МПа). Затем расширенный sCO₂ отдаёт тепло встречному потоку хладагента в рекуперативном теплообменнике LNG-100: 2–3 — изобарическое охлаждение (T3 = 189°C, P3 = 8 МПа). Далее хладагент передаёт теплоту отопительной воде в охладителе Е-100: 3–4 — изобарическое охлаждение sCO₂ до псевдокритической температуры без транскритического перехода (рис. 3б и 3в) вблизи линии насыщения в точке 4 (T4 = 34,63°C, P4 = 8 МПа). Затем давление и температура сверхкритической жидкости повышаются в компрессоре K-101 (рис. 3б и 3в): 4–5 — адиабатное сжатие (T5 = 88,9°C, P5 = 23 МПа). Затем sCO₂ дополнительно нагревается в теплообменнике-рекуператоре LNG-100: 5–6 — изобарический нагрев (T6 = 220°C, P6 = 23 МПа). Параметры потока хладагента из точки 6 передаются в цикле в точку 7. Далее sCO₂ нагревается в первичном теплообменнике E-101: 7–1 — изобарический нагрев (рис. 1б и 1в). Затем цикл повторяется. Полученные параметры потока хладагента в характерных точках цикла занесены в табл. 2.

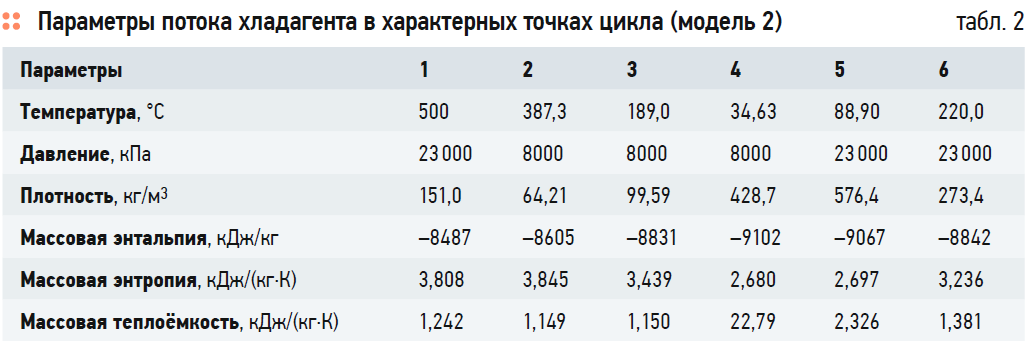
На рис. 3а также отдельно показаны конденсатор как теплообменник E-102 с входным и выходным потоками хладагента sCO₂ и теплоносителя (отопительной воды) и первичный теплообменник LNG-101 с входным и выходным потоками хладагента и теплоотдатчика (выхлопных газов), соответственно. Массовые расходы отопительной воды и выхлопных газов одинаковы с моделью 1 (4600 и 2200 кг/ч, соответственно). При этом вода нагревается от входной температуры 20°C до выходной температуры 70,43°C.

Оптимизация цикла при массовом расходе хладагента m* = 3600 кг/ч даёт мощность турбины Lтур = 118,4 кВт, мощность компрессора Lком = 35,08 кВт и мощность теплового потока в первичном теплообменнике Qтот = 355 кВт. При этом значение внутреннего КПД цикла:

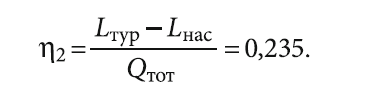
Известно, что, хотя эффективность обоих циклов, зависящая от мощности турбины, увеличивается с ростом температуры выхлопных газов, каждый цикл имеет диапазон температуры на входе турбины, в котором его эффективность выше. Так, цикл Брайтона более эффективен при температуре на входе турбины от 450°C и выше [12]. Однако сравнение результатов моделирования даёт η2 < η1, что объясняется ограничением на мощность турбины Lтур = 118 кВт, принятой в модели 2. В то же время высокая температура хладагента после турбины позволяет нагревать отопительную воду до температуры на 10°C выше, чем в модели 1. То есть, гибко меняя параметры цикла, можно настраивать ТНУ на желаемый результат.

Из табл. 2 видно, что между точками 3 и 4 плотность и теплоёмкость sCO₂ многократно возрастают, что объясняется достижением псевдокритической температуры при охлаждении. Этот процесс увеличивает теплообмен в газоохладителе и эффективность цикла в целом. Однако характер изменения характеристик sCO₂ между значениями на входе и на выходе из ГО зависит от его конструкции и режима работы. Подтвердить эффективность работы ГО можно моделированием протекающих в нём физических процессов. С этой целью проведено моделирование и исследование данного узла в ПО COMSOL Multiphysics.

Рассматривается U-образный теплообменник типа «труба в трубе», состоящий из нескольких параллельных трубок, собранных в пакет и помещённых внутрь U-образной внешней трубки. Хладагент sCO₂ движется по внутренним трубкам, а отопительная вода — в противоположном направлении по кольцевому зазору между ними и внешней трубкой. При расчёте такой конструкции ГО используется модель теплообменника «труба в трубе» равного объёма с эквивалентным диаметром dэкв = dN0,5, где d — диаметр трубки, N — число трубок в пакете [7].

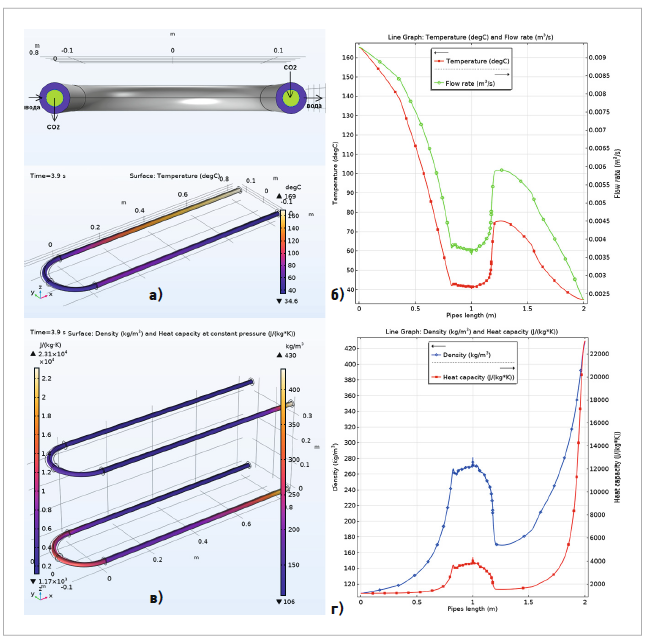
Рис. 4. Геометрия и функциональные характеристики U-образного трубчатого теплообменника [а — корпус с входными и выходными отверстиями и распределение температуры sCO2 в объёме внутренней трубы (3,9 с); б — распределение средней температуры и объёмного расхода хладагента по длине трубы; в — распределение плотности и массовой теплоёмкости хладагента в объёме внутренней трубы (3,9 с); г — то же для их средних значений по длине трубы]

Результаты моделирования ГО представлены на рис. 4. Геометрия, показанная на рис. 4а, ранее была построена в [7]. Длина внешней трубки — 2 м, длины прямых частей — 0,824 м, радиус кривизны изогнутого участка — 0,112 м, внутренний и внешний эквивалентный диаметры внутренней трубки — 16,5 и 21,8 мм. Указаны вход и выход sCO₂ — на торцах внутренней трубки, а также вход и выход отопительной воды — кольцевые зазоры между торцами трубок. Материал трубок — медь.

Параметры массового расхода и входной температуры хладагента и отопительной воды соответствуют модели 2. Их течение предполагается турбулентным. В интерфейсах Turbulent Flow, k-ε и Heat Transfer in Fluids решались уравнения теплообмена во временной области. Моделировалось начало процесса теплообмена в ГО на этапе пуска ТН после получения устойчивых параметров хладагента на выходе из компрессора. Время работы ГО до достижения температуры Tpc составило 3,9 с. На рис. 4а также показано распределение температуры хладагента в объёме внутренней трубы в момент времени 3,9 с. Видно, что остывание sCO₂ от входа во внутреннюю трубу с температурой 189°C происходит равномерно лишь на первом прямом участке (до температуры около 45°C), в то время как до середины дугового участка трубы температура почти постоянна, а к началу второго прямого отрезка возрастает почти до 75°C и лишь затем резко убывает до 34,63°C на выходе.

Аналогичные особенности имеет распределение средней температуры sCO₂ по длине трубы l, которое показано вместе с величиной объёмного расхода хладагента на рис. 4б. Хорошо заметна корреляция этих параметров на всех участках трубы: быстрое убывание на первом прямом отрезке, колебания на дуге от медленного уменьшения с минимумом при l = 1 м (45°C и 0,0026 м³/с, соответственно) до скачка величин с максимумом при l = 1,3 м (75°C и 0,0057 м³/с, соответственно) и последующее убывание на втором прямом отрезке. При постоянных массовом расходе и давлении хладагента на входе в ГО эти колебания вызваны изменением плотности и массовой теплоёмкости в объёме ГО.

На рис. 4в дано распределение плотности и массовой теплоёмкости sCO₂ в объёме внутренней трубы в момент времени 3,9 с. Видно, что их величины равномерно возрастают лишь на первом прямом участке: [до 265 кг/м³ и 3600 Дж/(кг·К), соответственно], а на дуге имеют максимум при l = 1 м [выше 250 кг/м³ и 4000 Дж/(кг·К), соответственно] с последующим падением до минимума при l = 1,3 м [около 170 кг/м³ и 1800 Дж/(кг·К), соответственно]. Рост на втором прямом участке даёт значения на выходе около 430 кг/м³ и 2200 Дж/(кг·К), соответственно. В целом распределение этих параметров соответствует распределению температуры (рис. 4а). Тем самым подтверждается значительная неравномерность изменения параметров sCO₂ при прохождении дугового участка трубы.

На рис. 4 г. показано распределение средней плотности и массовой теплоёмкости sCO₂ по длине трубы. Видны все особенности, отмеченные выше, причём в середине дугового участка трубы (l = 1 м) эти величины имеют острый пик [280 кг/м³ и 4500 Дж/(кг·К), соответственно]. Значения на выходе из трубы [425 кг/м³ и 2250 Дж/(кг·К)] близки к указанным в табл. 2.

Таким образом, эффективность теплообмена в U-образном газоохладителе при температурах, близких к псевдокритической, существенно зависит от формы трубок и режима течения sCO₂. Нахождение оптимальных условий потребует дополнительных исследований.

Заключение

1. Анализ использования в современных условиях развития экономики страны мини-ТЭЦ для снабжения электрической и тепловой энергией ряда хозяйственных объектов показал, что возможно получение значительного эффекта в следующих направлениях производственной деятельности: утилизация отходов деревопереработки, сельского хозяйства и ТБО; утилизация сбросовой тепловой энергии технологических процессов; ускоренный ввод энергетических мощностей для реализации новых бизнес-проектов, в том числе в развивающейся сфере быта, а также стабилизации функционирования предприятий жилищно-коммунального хозяйства.

2. Косвенным, но весьма значимым результатом более широкого применения мини-ТЭЦ можно считать обеспечение высокой надёжности использования электроэнергии населением, например, путём замены газовых бытовых плит на электрические (в некоторых, особых случаях), тем самым исключаются угрозы из-за неправильной эксплуатации газового оборудования, несоблюдения регламентных работ по обслуживанию и ремонту его газовой службой и других случайных явлений, связанных с газовым оборудованием в быту.

3. Представлены методики моделирования термодинамических циклов в ПО Aspen HYSYS для тепловых насосов, работающих от выхлопных газов двигателя внутреннего сгорания мини-ТЭЦ на хладагенте R744 (CO₂) на основе цикла Ренкина в транскритической области и цикла Брайтона в сверхкритической области. Это позволяет потребителю осуществлять надёжный выбор мини-ТЭЦ необходимой мощности с учётом особенностей функциональных характеристик термодинамического цикла.

4. Проведено моделирование и исследование принципиальной структурной схемы первичного теплообменника в ПО COMSOL Multiphysics в виде трубчатого змеевика, устанавливаемого в глушителе выхлопной трубы двигателя внутреннего сгорания мини-ТЭЦ. Показано, что теплообмен с потоками выхлопных газов с температурой 400–450°C позволяет нагревать хладагент R744 до температуры до 300°C, необходимой для обеспечения работоспособности смоделированной ТНУ по технологии цикла Ренкина.

5. Методика моделирования структурной схемы ТНУ по технологии цикла Брайтона отличается в узлах газоохладителя и компрессора, но остаётся практически без изменений для первичного теплообменника, за исключением увеличения числа витков трубчатого змеевика (примерно на 5–10%) и дополнительного исследования на работоспособность функционирования.

6. Моделирование и исследование в ПО COMSOL Multiphysics газоохладителя в виде U-образного теплообменника типа «труба в трубе» показало, что оптимизация функциональных характеристик ТНУ на основе цикла Брайтона может быть связана с дополнительными исследованиями распределения плотности и удельной теплоёмкости sCO₂ в объёме теплообменника при температурах, близких к псевдокритической.