Статья ВАК: Моделирование и исследование в COMSOL Multiphysics динамических характеристик малых ветроэнергетических установок

Введение

В настоящее время значительное усложнение конструкций многих изделий машиностроения потребовало от разработчиков использования новых методов их проектирования. Это связано прежде всего с требованиями сокращения сроков создания изделий. В то же время уровень сложности изделий стал существенно влиять на эффективность труда проектировщика. Оказалось, что технические требования к изделиям уже не могут быть обеспечены без интенсивного использования компьютерных технологий в процессе их проектирования, конструирования и изготовления. Следствием этого стало появление нового инженерного инструмента — систем автоматизированного проектирования (САПР), широко опирающихся на всех этапах производства новой техники на программные комплексы компьютерного инженерного анализа (САЕ), основанные на методе конечных элементов (МКЭ). Примерами комплексов САЕ являются пакеты программ высокого уровня, например, ANSYS, SolidWorks, COMSOL Multiphysics. Они позволяют численно, с достаточно высокой точностью приближения в зависимости от уровня детализации расчётной сетки, решать самые разнообразные задачи из самых различных областей физики, например, механики твёрдого тела, аэродинамики, термодинамики, теплопередачи и многих других.

Виртуальная (цифровая) модель реального объекта выражает его ключевые характеристики и способна воспроизводить его функции при разных условиях. По сути, это совокупность математических формул, описывающих сам объект и протекающие в нём процессы. При этом построенная таким образом цифровая модель отличается более высокой точностью кинематических и функциональных связей, чем в реальном объекте, построенном при использовании, например, производственной поузловой сборки.

Дальнейшее совершенствование методов создания новой техники привело к появлению при проектировании обновляемых взаимосвязей между реальным и виртуальным объектами концепции «цифрового двойника» (digital twin) [1, 2].

Эта концепция предполагает, что виртуальный объект содержит подробное (обычно численное) описание физического устройства или процесса и получает всю информацию, собранную от реального объекта в виде показаний датчиков, отчётов пользователей и других данных. Таким образом, цифровой двойник должен быть динамическим и постоянно обновляемым представлением реального физического устройства или процесса, перенесённым в виртуальную среду. В свою очередь, различные прогнозы, оценки и управляющие параметры, которые могут использоваться для разработки и эксплуатации реального устройства, должны непрерывно передаваться обратно из виртуального пространства в реальное. Статическая модель не является цифровым двойником.

Метод применения цифрового двойника в промышленности был известен и раньше. Но лишь появление достаточных вычислительных мощностей для проведения комплекса расчётов в реальном времени позволило расширить применение метода, например, уже на этапе эскизного проектирования. Использование ПО для имитационного моделирования позволяет обновлять системную модель и создавать её вариации. Далее на этапе технического проектирования полученная на предыдущем этапе модель может дорабатываться и уточняться при помощи более точных системных моделей элементов на основе данных, непрерывно получаемых при дополнительных исследованиях цифровых моделей. При этом используются также показания датчиков от реального объекта и информация о его текущем техническом состоянии. На этапе изготовления разработанный цифровой двойник изделия помогает в определении допусков и контроле точности характеристик для безотказной работы изделия, причём в течение всего срока службы.

Таким образом, цифровой двойник практически сопровождает реальный объект в течение всего его жизненного цикла. За это время непрерывно создаётся научно-техническая база для выпуска в перспективе подобных объектов с новыми, более эффективными технико-экономическими характеристиками.

Ветроэнергетические установки (ВЭУ) в целом представляют собой достаточно сложные объекты с неустоявшимися ещё конструктивными параметрами и функциональными характеристиками, требующие непрерывного совершенствования и постоянного инженерного внимания. Так, на ВЭУ башенного (мачтового) типа с горизонтальной осью вращения ветрового колеса (ВК) действуют разнообразные нагрузки: от собственного веса элементов ВЭУ; ветровые нагрузки на ВК и мачту; динамические нагрузки от гироскопического момента при вращении ВК на гондолу ВЭУ; центробежные силы, вызванные дисбалансом массы ВК по отношению к оси вращения; и другие. Центробежные силы дисбаланса могут достигать значительной величины и практически присутствуют во всех ВК, созданных в том числе в заводских условиях [3].

По данным проведённых ранее исследований [4], эксцентриситет центра масс ВК по отношению к его геометрическому центру на оси вращения может составлять до 0,25% диаметра ВК. Это создаёт дисбаланс массы ВК и вызывает при его вращении динамические нагрузки, передаваемые через ступицу вала ВК на его подшипниковые опоры и, следовательно, на мачту и фундамент ВЭУ, оказывая наиболее существенное влияние на снижение надёжности функционирования ВЭУ.

В связи с этим, в данной работе рассматриваются вопросы моделирования и исследования динамических характеристик малых ВЭУ, с учётом наличия дисбаланса ВК. На основе представленной выше концепции с использованием ПО SolidWorks и COMSOL Multiphysics моделировалась геометрия ВК. Далее определялся центр масс виртуальной модели и исследовались её динамические характеристики, в том числе действие дисбаланса (если он присутствовал в данной модели). Далее виртуальная модель ветроколеса рассматривалась в качестве цифрового двойника и исследовались её динамические характеристики с учётом конструктивных параметров реальной модели, то есть наличия возможного дисбаланса ВК, в соответствии с существующими методиками [4, 5]. Затем отрабатывалась методика балансировки реального ВК до совпадения показателей динамических характеристик с цифровой моделью.

Исследуемая модель и результаты

Геометрия исследуемой модели включает три лопасти аэродинамического профиля NACA 44–12, часто используемого в малых ВЭУ. Трёхмерная модель лопасти длиной 3,5 м построена в ПО SolidWorks по десяти перпендикулярным сечениям в соответствии с формулами, задающими наиболее эффективные параметры лопасти с точки зрения аэродинамики [6]. Длины хорд сечений и углы закрутки уменьшаются от основания к вершине от 0,6322 до 0,1688 м и от 34,11° до 1,06°, соответственно. Угол атаки, оптимальный для данного профиля, равен 5,25°. Цилиндрические основания лопастей длиной 0,35 м закреплены в соответствующих отверстиях ротора гондолы. Ротор жёстко посажен на вал, помещённый в два подшипника, которые установлены в опорах в виде стоек на плите гондолы. Дальнейшее моделирование динамики ветроколеса проводилось в ПО COMSOL Multiphysics по методике, принятой в работах [7, 8]. Однако лопасти предполагаются цельнометаллическими, как и прочие элементы ВК. Поэтому использовался интерфейс Multibody Dynamics, причём для лопастей и ротора — с узлом Rigid Domain, а для вала, подшипников и их опор — с материальной моделью Linear Elastic Material. Моделировалось вращение ВК от начального состояния покоя до выхода на устойчивый режим работы с постоянной скоростью вращения 60 об/мин. вокруг оси Oz в продолжение двух оборотов (2 с).

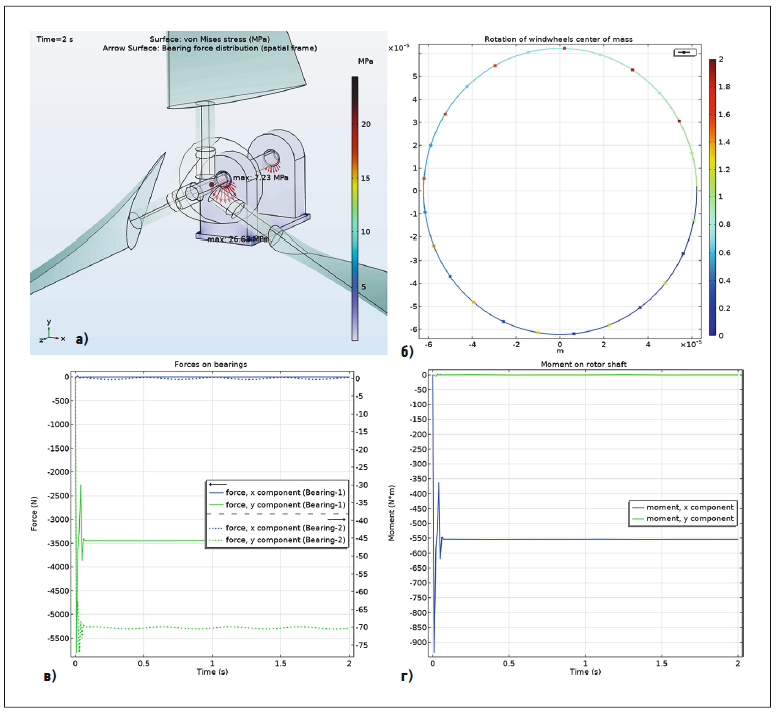
Рис. 1. Геометрия ВК без дисбаланса и функциональные характеристики цифровой модели [а — геометрия ВК (фрагмент в увеличенном масштабе), центр масс — точка на оси вращения ВК, напряжения и распределение сил на первой и второй опорах вала (2 с); б — траектория движения центра масс ВК (в увеличенном масштабе); в — составляющие нагрузки на опорах вала по осям Ox и Oy; г — составляющие момента сил на валу ротора по осям Ox и Oy]

Результатом первого этапа исследования геометрии ВК, построенной по аналитическим зависимостям (рис. 1), является определение центра масс ВК, напряжений и нагрузок на опорах вала ВК под действием сил, передаваемых валом при вращении ВК на подшипниковые опоры. Как было отмечено выше, моделирование МКЭ даёт приближенный результат, что обусловлено возможными незначительными погрешностями в геометрии модели и уровнем детализации расчётной сетки, но в то же время с точностью, достаточной для инженерных расчётов. На рис. 1а показана геометрия ВК, центр масс — точка на оси вращения ВК, напряжения и распределение сил на опорах подшипников. Установлено, что центр масс ВК лежит практически на геометрической оси вращения ВК и смещение его пренебрежимо мало. Максимальное напряжение на первой подшипниковой опоре за пол-оборота вала (время 0,5 с) под действием веса ВК равно 26,64 МПа, а на второй опоре значительно меньше — 7,24 МПа. Можно заметить, что напряжения на опорах при вращении ВК остаются постоянными в моменты времени, кратные полупериоду: 1,0; 1,5 и 2,0 с. Это показывает практическое отсутствие дисбаланса в геометрии ВК. Характер распределения сил на опорах вала — типичный для подшипников (эпюра сил косинусоидального вида).

На рис. 1б дана в увеличенном масштабе траектория движения центра масс при вращении ВК. Отклонение центра масс ВК от оси вращения всего лишь 0,06 мм, что не может существенно отражаться на динамических характеристиках ВЭУ.

Изменение нагрузки на валу ВК в области подшипниковых опор можно оценить более детально. На рис. 1в показаны составляющие по осям Ox и Oy сил, действующих на опорах. По оси Oz нагрузка не передаётся, её составляющая равна 0 и не показана. В начале вращения ВК наблюдается всплеск колебаний нагрузки на первую опору вала с высокой амплитудой по оси Oy. Далее на первой опоре по оси Ox нагрузка практически отсутствует, есть лишь незначительные колебания относительно нулевой линии, а по оси Oy под действием силы веса ВК наступает стабилизация нагрузки со значением около −3440 Н (сплошные линии). На второй опоре по оси Ox нагрузка в среднем также близка к нулю с небольшими колебаниями (синяя пунктирная линия). По оси Oy изменение нагрузки также представлено гармоническими колебаниями с малой амплитудой и средним значением около −70 Н (зелёная пунктирная линия). Частота колебаний по обеим осям вдвое выше частоты вращения ВК 6,28 Гц, причём колебания второй опоры по оси Ox находятся в противофазе с колебаниями по той же оси первой опоры. Это объясняется тем, что опоры расположены на некотором расстоянии друг от друга, и вал получает, хотя и незначительные, периодические изгибные колебания той же формы, передавая нагрузку между опорами со смещением фазы. В то же время надо отметить, что незначительные гармонические колебания нагрузки по осям Ox и Oy являются следствием смещения центра масс от оси Oz на 0,06 мм.

На рис. 1 г. даны составляющие момента сил на валу ротора. По оси Ox момент остаётся постоянным со значением около −550 Н·м. По оси Oy момент равен нулю. Таким образом показано, что при вращении ВК, построенного по аналитическим зависимостям, возможны незначительные отклонения (практически пренебрежимо малые) при исследовании динамических характеристик средствами ПО COMSOL Multiphysics. Они не могут оказать существенного влияния на результаты задачи первого этапа — исследование динамических характеристик ВК виртуальной модели. В связи с этим, данная геометрия может выступать цифровой моделью для изучения и других видов нагрузок и процессов на ВК при вращательном движении.

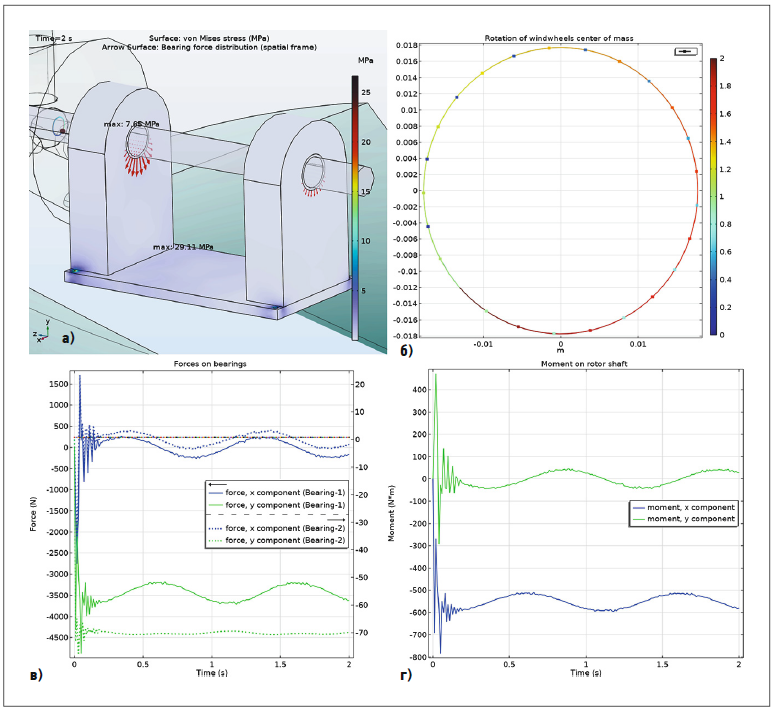
Рис. 2. Геометрия ВК с дисбалансом и функциональные характеристики цифровой модели [а — геометрия ВК (фрагмент в увеличенном масштабе), траектория вращения центра масс ВК вокруг оси Oz, напряжения и распределение сил на первой и второй опорах вала (2 с); б — траектория движения центра масс ВК (в увеличенном масштабе); в — составляющие нагрузки на опорах вала по осям Ox и Oy; г — составляющие момента сил на валу ротора по осям Ox и Oy]

Вторым этапом исследования динамических характеристик малых ВЭУ стало исследование цифровой модели ВК с дисбалансом (рис. 2). Как было указано выше, при поузловой сборке ВК в производственных условиях эксцентриситет центра масс ВК по отношению к геометрическому центру может составлять до 0,25% диаметра ВК. При этом заранее предсказать неуравновешенность тех или иных элементов ВК при сборке практически невозможно (это случайное событие), и суммарная величина дисбаланса проявляется только в процессе установки ВК на ступицу вала гондолы при пробной прокрутке. Поэтому неуравновешенность ВК в цифровой модели задавалась искусственно путём изменения положения центров масс каждой из лопастей. Для этого их координаты получали поправки в виде псевдослучайных чисел, заданных функцией Random с равномерным распределением. Далее определялся эксцентриситет центра масс ВК относительно его оси вращения, который составил 17,7 мм, что соответствует его возможной величине при диаметре ВК, равном 7 м. Затем вновь находились характеристики напряжений и нагрузок на опорах вала ВК.

На рис. 2а показаны геометрия ВК, траектория вращения центра масс ВК вокруг оси Oz, напряжения и распределение сил на первой и второй опорах вала при вращении ВК. Установлено, что при вращении ВК центр масс описывает окружность радиусом 17,7 мм. Максимальное напряжение на первой опоре за пол-оборота вала (0,5 с) равно 24,09 МПа, на второй значительно меньше — 6,8 МПа. Вал ВК передаёт нагрузки через подшипники на опоры и далее на плиту гондолы.

Максимальные напряжения на опорах вала в моменты времени 1,0; 1,5 и 2 с на первой опоре: 29; 24,19 и 29,11 МПа; на второй опоре — 7,66; 6,81 и 7,65 МПа, соответственно. Итак, при наличии дисбаланса напряжения на опорах вала ВК непостоянны и изменяются периодически. Следовательно, периодическое изменение напряжений будет передаваться на плиту гондолы, мачту и фундамент ВЭУ.

Траектория движения центра масс в увеличенном масштабе показана на рис. 2б. Отклонение центра масс ВК от оси вращения равно 17,7 мм, что может заметно повлиять на динамические характеристики ВЭУ.

Периодичность нагружения вала в области подшипниковых опор наглядно можно наблюдать на рис. 2в. Здесь показаны составляющие по осям Ox и Oy сил, действующих на опоры. В момент пуска ВК происходит высокочастотный всплеск колебаний нагрузки на обе опоры вала с быстро затухающей амплитудой по обеим осям. На первой опоре по оси Ox за счёт действия дисбаланса ВК устанавливаются гармонические колебания нагрузки вокруг нулевого значения с частотой, равной частоте вращения ВК 6,28 Гц, и амплитудой 238 Н (сплошная синяя линия). Максимум нагрузки показан горизонтальной линией. Аналогично по оси Oy под действием силы веса ВК наступает стабилизация при значении примерно −3440 Н. Далее происходят гармонические колебания нагрузки с теми же частотой 6,28 Гц и амплитудой 238 Н, но со сдвигом по фазе примерно на 0,25 с за счёт смещения центра масс ВК относительно осей (сплошная зелёная линия). Общая нагрузка возрастает по абсолютной величине за каждый цикл вращения ВК до 3680 Н. По оси Oz (вдоль вала) колебания нагрузки не передаются. Составляющие сил, действующих на второй опоре, показаны пунктиром. По оси Ox устанавливаются гармонические колебания нагрузки относительно нулевой линии с частотой 6,28 Гц и амплитудой примерно 4 Н. По оси Oy нагрузка со средним значением около −70 Н также испытывает колебания с малой амплитудой и частотой вдвое выше частоты вращения ВК.

Кроме того, колебания нагрузки на второй опоре по оси Ox совпадают по фазе с колебаниями по той же оси на первой опоре, а по оси Oy находятся практически в противофазе с колебаниями по той же оси на первой опоре. Это также объясняется изгибными колебаниями вала, который передаёт нагрузку между опорами. Со временем это может привести к усталостным явлениям в металле вала.

На рис. 2 г. даны составляющие момента сил на валу ротора. По оси Ox гармонические колебания момента с частотой 6,28 Гц устанавливаются относительно значения примерно −550 Н·м с амплитудой примерно 90 Н·м. По оси Oy — относительно нулевого значения с той же частотой 6,28 Гц и амплитудой примерно 40 Н·м. Причём колебания момента на валу по каждой из осей находятся в противофазе с колебаниями нагрузки на первой опоре.

Данная цифровая модель позволяет также проводить исследование деталей ВК на прочность и циклическую усталость в зависимости от времени эксплуатации объекта.

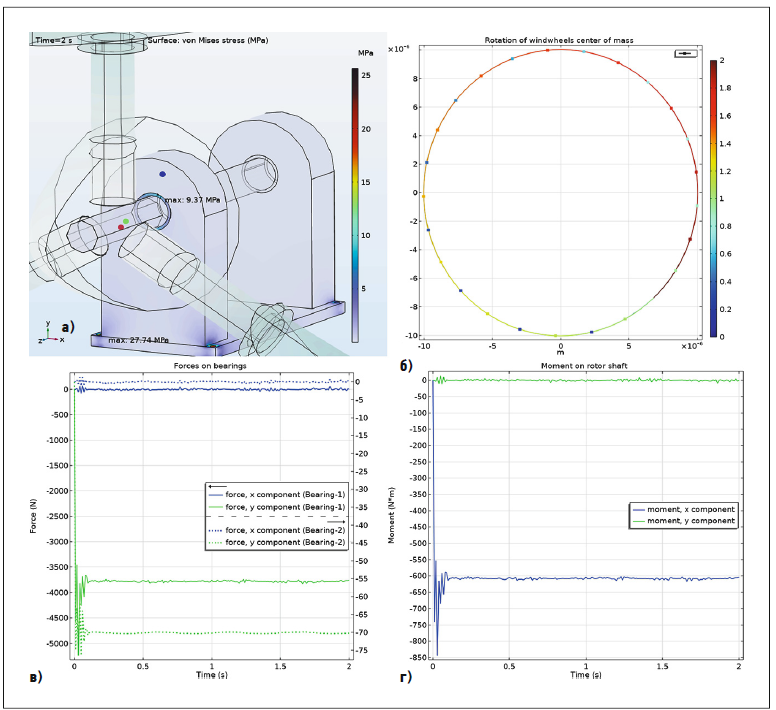
Рис. 3. Геометрия ВК после статической балансировки и функциональные характеристики цифровой модели [а — геометрия ВК (фрагмент в увеличенном масштабе), центр масс — точка на оси вращения ВК, напряжения на первой и второй опорах вала (2 с); б — траектория движения центра масс ВК (в увеличенном масштабе); в — составляющие нагрузки на опорах вала по осям Ox и Oy; г — составляющие момента сил на валу ротора по осям Ox и Oy]

На третьем этапе проводилось исследование цифровой модели ветрового колеса при выполнении статической балансировки (рис. 3). Известно, что если центр тяжести ВК имеет эксцентриситет e относительно оси вращения, то при вращении ВК возникает центробежная сила инерции с амплитудой

Fи = mω2е,

где m — масса ВК; ω — угловая скорость вращения [4]. В данной цифровой модели при e = 17,7 мм, m = 340,03 кг, ω = 6,28 с-1, Fи = 238,07 Н. Это соответствует величине амплитуды гармонических колебаний нагрузки на рис. 2в. Как показано на рис. 2в и 2 г., действие этой силы на подшипники, в которых вращается вал ВК, а следовательно, и на плиту гондолы, и на мачту ВЭУ, и её фундамент является периодическим. Координаты смещённого центра масс ВК (красная точка на рис. 3а) по осям Ox и Oy равны −0,012 и −0,013 м, соответственно. Для устранения статической неуравновешенности необходимо на противоположную относительно оси вращения ВК сторону добавить противовес (синяя точка) массой mп, на некотором расстоянии rп от оси вращения Oz, чтобы алгебраическая сумма статических моментов масс была равна нулю, то есть mпrп = mе. При этом, чем больше rп, тем меньше значение массы mп балансировочного груза. Поэтому в данном случае, как и делается обычно на практике, дополнительные грузы устанавливались не на поверхности ротора, а на цилиндрических основаниях двух лопастей — в виде колец, rп = 0,34 м. Величины добавленных масс легко определить по правилу параллелограмма для суммы векторов.

Результатом третьего этапа исследования цифровой модели стало практически полное совпадение функциональных характеристики ВК с первым (рис. 1) этапом исследования. На рис. 3а показана геометрия ВК, центр масс — точка на оси вращения ВК (зелёная точка), напряжения и распределение сил на опорах подшипников. Установлено, что центр масс после балансировки лежит практически на оси Oz и смещение его не превышает точности расчёта. Это видно в увеличенном масштабе и на рис. 3б. Напряжения на опорах вала остаются постоянными в моменты времени, кратные полупериоду. В моменты времени 0,5; 1,0; 1,5 и 2 с на первой опоре ВК напряжение равно 27,74 МПа при значительно меньшем напряжении на второй опоре — 9,37 МПа. На рис. 3в показаны составляющие по осям Ox и Oy сил, действующих на опорах. Видно, что нагрузки по оси Ox на обеих опорах равны нулю (синие линии), стабилизация нагрузки по оси Oy на первой опоре достигается при значении около −3700 Н (действие силы веса ВК), а на второй опоре — около −70 Н (зелёные линии). Периодические колебания нагрузок практически не отмечены, лишь по оси Oy на второй опоре, как и на рис. 1в, присутствуют колебания с малой амплитудой и частотой вдвое выше частоты вращения ВК.

На рис. 3 г. даны составляющие момента сил на валу ротора. По оси Ox момент остаётся постоянным со значением примерно −610 Н·м. По оси Oy момент сил на валу ротора равен нулю.

Статическая балансировка ВК малых ВЭУ часто считается заключительной операцией по исследованию нагрузок, действующих на элементы его конструкции. Это обусловлено невысокой скоростью вращения ВК, в данном случае лишь 60 об/мин.

Поэтому можно ожидать, что одномоментное динамическое воздействие на элементы конструкции будет не столь значительным. Однако в течение длительной эксплуатации ВЭУ эти воздействия могут существенно отразиться на снижении характеристик функционирования и надёжности эксплуатации установок. Одним из признаков необходимости исследования динамической неуравновешенности ВК является обнаружение, например, нестабильности нагрузки (напряжений) на опорах ВК в течение полного оборота его вала. Причиной может быть действие момента силы относительно оси его вращения. Для этого необходимо определить центры масс верхней и нижней половины ВК. Если они лежат в одной плоскости, перпендикулярной оси вращения, то ВК можно считать динамически уравновешенным. Если в разных плоскостях, на расстояниях r1 и r2 от оси вращения, то необходимо проводить динамическое уравновешивание [9]. В нашем случае верхняя и нижняя половины ВК с массами mв и mн имеют центры масс в разных плоскостях вращения, причём mв ≠ mн и r1 ≠ r2.

При вращении динамически неуравновешенного ВК с угловой скоростью ω возникают центробежные силы инерции Fи1 и Fи2. Они образуют пару сил с моментами М1 = Fи1L1 и М2 = Fи2L2, где Li — расстояния от центров масс половин ВК до плоскости вращения общего центра тяжести (i = {1, 2}). Под их действием ВК стремится повернуться вокруг оси Ox, вследствие чего на подшипники вала будут действовать дополнительные силы, вызывающие вибрацию. Для динамического уравновешивания моментов М1 и M2 используют противовесы, располагая их чаще всего на боковых поверхностях ротора ВК или на цилиндрических основаниях лопастей, или же распределяют противовесы по тем и другим местам так, чтобы они образовывали пару сил с моментами противоположного направления. При этом как алгебраическая сумма статических моментов масс, так и геометрическая сумма моментов центробежных сил инерции должны быть равны нулю.

Противовес моменту М1 был создан двумя грузами, закреплёнными на верхней поверхности ротора и на его торце вблизи вала, общей массой m = 11,25 кг с эффективным плечом l1 = 0,051 м, а противовес моменту М2 — грузом той же массы m на нижней поверхности ротора с плечом l2 = 0,0507 м.

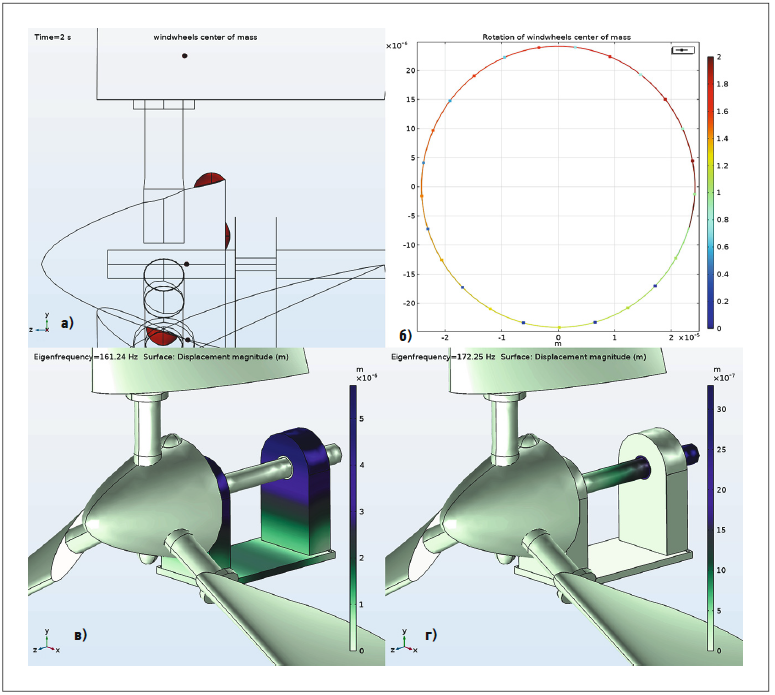
Рис. 4. Геометрия ВК после динамической балансировки и функциональные характеристики цифровой модели [а — геометрия ВК (фрагмент в увеличенном масштабе), центр масс ВК, его верхней и нижней половины — точки в различных плоскостях вращения и добавленные грузы; б — траектория движения центра масс ВК (в увеличенном масштабе); в — смещение элементов ВК при колебаниях на первой собственной частоте; г — то же для второй собственной частоты]

Функциональные характеристики цифровой модели после динамического уравновешивания ВК оказались близки к полученным на первом этапе исследования, поэтому на рис. 4 приводятся некоторые новые результаты. На рис. 4а показаны центр масс ВК, его верхней и нижней половины до динамической балансировки и добавленные для этой балансировки грузы. Центр масс всего ВК остался также практически на оси вращения со смещением около 0,02 мм — величиной, определяемой точностью расчёта (рис. 4б).

На рис. 4в и 4 г. показано смещение (деформация) элементов ВК при колебаниях на первой (161,24 Гц) и второй (172,25 Гц) собственных частотах. Видно, что в первом случае напряжённо-деформированное состояние могут испытывать элементы стоек и плиты гондолы ВЭУ. Во втором случае это происходит только на валу ВК с возрастанием величины деформации в зоне второй опоры. Но в численном выражении указанные явления незначительны, как можно судить по графику деформации. Кроме того, отмеченные стальные элементы ВК имеют значительный запас прочности, что видно по результатам второго этапа исследований (рис. 2а). В то же время при проектировании ВЭУ важным является обеспечение устойчивости системы «ВЭУ — фундамент». Задача устойчивости мачт малых ВЭУ исследовалась в [10]. Для обеспечения устойчивости системы «ВЭУ-фундамент» требуется, чтобы частота её собственных колебаний не попадала в резонанс с частотой вращения ВК. Для этого достаточно, чтобы для наименьшей собственной частоты ω1 и наибольшей частоты вращения ВК ωmax выполнялось условие ωmax/ω1 ≤ 0,577. Система, для которой выполняется это условие, считается жёсткой [5]. Наибольшая рабочая частота вращения ВК определяется геометрией лопасти и конструкцией ВК [8]. В нашем случае ω1 = 161,24 Гц, ωmax = 34,3 Гц, так что условие заведомо выполняется.

Таким образом, цифровая модель, построенная в ПО COMSOL Multiphysics, позволяет оперативно и с высокой точностью проводить значительный ряд исследований механических и физических процессов, протекающих в узлах и механизмах ВЭУ, заменяя затратные натурные испытания на действующих объектах.

Заключение

1. Малые ВЭУ — это сложные структурные и конструктивные объекты с недостаточно ещё отработанными параметрами и функциональными характеристиками, требующие непрерывного совершенствования и постоянного инженерного внимания. Для дальнейшего развития их необходима цифровая модель конструкции, сопровождающая реальный объект в течение всего жизненного цикла. В этот период возможны плановые регламентные работы и процедурные доработки на реальном объекте на основании результатов проведённых ранее исследований на цифровой модели. Кроме того, за это время будет создаваться научно-техническая база для выпуска подобных объектов с новыми, более эффективными технико-экономическими параметрами.

2. На малые ВЭУ мачтового типа с горизонтальной осью вращения ВК действуют разнообразные нагрузки: это нагрузки от собственного веса элементов ВЭУ, ветровые нагрузки на ВК и мачту, динамические нагрузки от дисбаланса массы ВК по отношению к оси вращения, приводящие к циклическим изменениям нагрузки на подшипниковых опорах ВК, передаваемые далее на мачту и фундамент ВЭУ и оказывающие наиболее существенное влияние на снижение надёжности установок.

3. Разработка цифровой модели ВК малых ВЭУ в ПО COMSOL Multiphysics, использующем средства комплексного компьютерного инженерного анализа (САЕ), позволило провести исследование влияния дисбаланса ВК, часто встречающееся в реальных их конструкциях, и получить достоверные значения действующих сил и напряжений на опорах вала ветроколеса, что обусловило необходимость поиска теоретических и практических основ уравновешивания массы ВК. Данная цифровая модель позволяет проводить исследования на прочность, усталость, надёжность элементов ВК, а также эффективность аэродинамики лопастей и функциональных характеристик малых ВЭУ.

4. Разработан статический метод уравновешивания (балансировки) ВК в ПО COMSOL Multiphysics. Предложен алгоритм определения места положения центра масс ВК с дисбалансом, определена центробежная сила инерции Fи, вызванная его действием, которая уравновешивается расчётной массой противовеса mп, размещённого на противоположной стороне от оси вращения ВК. В этом случае дополнительные грузы устанавливались не на поверхности ротора, а на цилиндрических основаниях двух лопастей. Алгебраическая сумма статических моментов масс стала равна нулю, что обеспечило статическое уравновешивание масс ВК.

5. Разработан динамический метод уравновешивания (балансировки) ВК в ПО COMSOL Multiphysics. Предложен алгоритм определения места положения центра масс верхней и нижней половинок ВК. Установлено, что они расположены в разных плоскостях вращения, вследствие чего возникают моменты сил инерции М1 и М2. Под их действием ВК стремится повернуться вокруг оси Ox, что приводит к возникновению на подшипниках вала дополнительной нагрузки. Для динамического уравновешивания ВК рассчитывалась система противовесов, один из которых массой m распределён между верхней поверхностью ротора и его торцом вблизи вала, а второй той же массы на нижней поверхности ротора. Таким образом создавалась пара сил с моментами, направленными противоположно М1 и М2, что обеспечило динамическую уравновешенность ветроколеса.