Статья ВАК: Метод оценки эффективности модернизации теплообменных поверхностей отопительных приборов. Проверка базовой модели

На данный момент эффективность работы отопительных приборов оценивается исходя из результатов натурных испытаний согласно [1]. Определяется тепловой поток и далее привязывается к массовым, объёмным или габаритным характеристикам отопительного прибора.

Также большинство методов испытаний отопительных приборов, применяемых на практике, оперируют исключительно интегральными показателями, так как определение эффективности работы сложной теплообменной поверхности при естественной конвекции представляется исключительно сложной задачей. Классические методы анализа естественной конвекции, вроде решения Польгаузена [2] или аналитического решения Бар-Коэна и Розеноу [3], не дают возможности применять их при работе естественной конвекции даже на относительно простых поверхностях, поскольку решения фактически являются двумерными и применимыми только для симметричных систем. В то время как реальные методы интенсификации естественной конвекции, применяемые в отопительных приборах, предполагают развитие поверхности путём нанесения сложных интенсификаторов, оребрения сложной формы, специальных направляющих и т. п. Анализ поведения теплового потока в подобных системах лежит в области не только теплообмена, но и массообмена.

В работе предлагается проверка численной модели путём сравнения её результатов с данными поставщика отопительного оборудования, полученными в лаборатории. На базе полученных результатов, возможно, будет развит метод оценки эффективности модернизации теплообменных поверхностей отопительных приборов путём совмещения аналитических расчётов и численного моделирования и последующего сравнения их с результатами натурного моделирования.

Постановка задачи

Рассматриваем стандартный отопительный прибор «тип 22» размерами 500×1000 мм конструкции, показанной на рис. 1. Параметры конвективной ленты радиатора представлены на рис. 2.

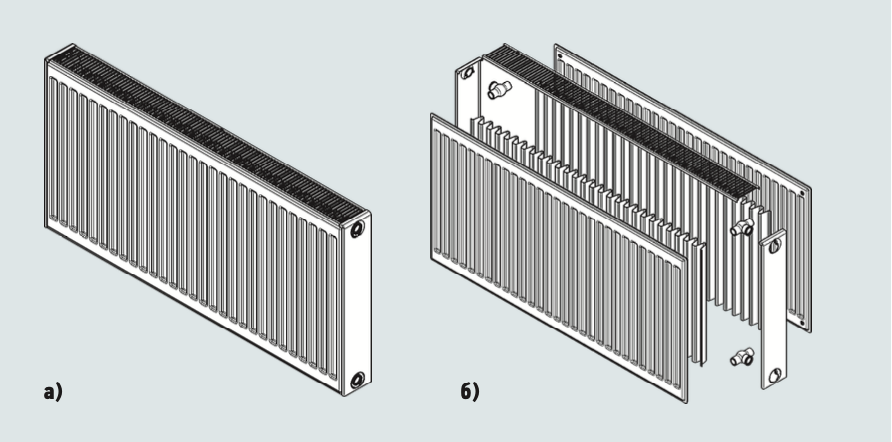
Рис. 1. Конструкция стального панельного отопительного прибора «тип 22» (а — в собран‐ ном виде, б — схема: 1 — греющий элемент; 2 — распределительные трубки; 3 — боковые экра‐ ны; 4 — верхняя решётка; 5 — конвективная лента; 7 — отверстия для патрубков теплоносителя)

Из данных [4] тепловой поток от отопительного прибора при температуре окружающего воздуха +20°C, температурах входа и выхода теплоносителя +85°C и +75°C, соответственно (средняя температура +80°C, разница температур между теплоносителем и окружающим воздухом равна ∆t = 60°C), составляет 1,809 кВт. Данные подтверждены испытаниями в аккредитованной лаборатории, точность приведённых данных составляет 9% от величины теплового потока согласно п. 5.4.5 ГОСТ 31311–2005 [5], то есть реальный тепловой поток будет находиться в диапазоне 1,737–1,899 кВт.

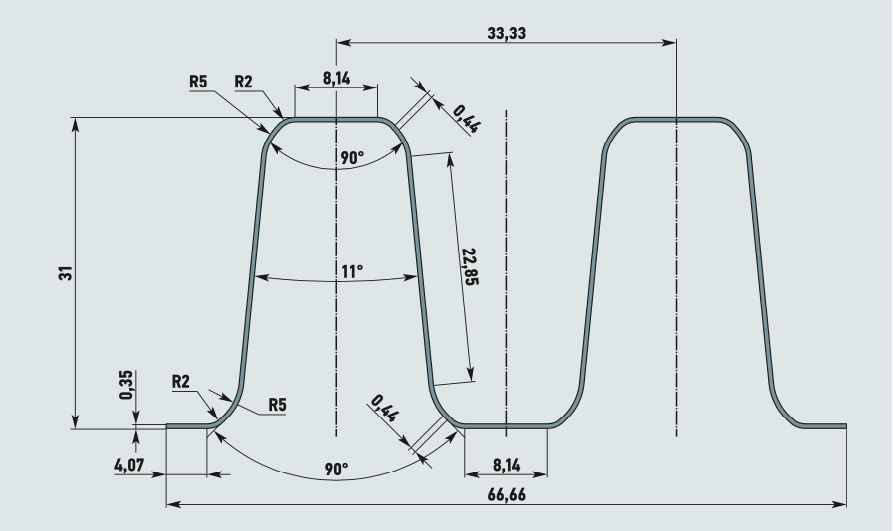
Рис. 2. Конвективная лента отопительного прибора

Предлагается построить аналитическую модель расчёта величины теплового потока от рассматриваемого отопительного прибора, с целью дальнейший оценки эффективности тех или иных мероприятий по увеличению теплового потока, через относительные величины.

Расчёт теплоотдачи отопительного прибора через критериальные уравнения с применением численного моделирования

Произведём расчёт теплоотдачи отопительного прибора по приведённой ниже методике:

Q = Qвн + Qвнеш + Qизл, (1)

где Qвн — количество тепла, передаваемое конвекцией от внутренних поверхностей радиатора (при движении воздуха за счёт естественной конвекции через конвективную ленту отопительного прибора), Вт; Qвнеш — количество тепла, передаваемое конвекцией от наружных поверхностей отопительного прибора, Вт; Qизл — тепло, передаваемое излучением от наружных поверхностей отопительного прибора, Вт.

Излучение, передаваемое внутренним пространством отопительного прибора (области расположения конвективной ленты), не учитываем, поскольку внутренние поверхности замыкают его сами на себя.

Таким образом, рассчитав каждую из составляющих, можем понять общий тепловой поток. Наибольшую сложность будет представлять из себя расчёт Qвн, поскольку конвективное движение внутри отопительного прибора имеет довольно сложную структуру. Поэтому воспользуемся методом численного моделирования, применив специализированный программный комплекс и задав граничные условия первого рода для нагрева, с применением двухслойной k-ε-модели турбулентности [6, 7] (данная модель турбулентности даёт хорошие результаты при расчёте теплообмена при течении в ограниченных каналах).

Краткое описание модели

Стандартное уравнение k-ε-модели турбулентности для энергии имеет следующий вид:

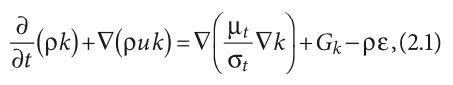
здесь k — кинетическая энергия турбулентных пульсаций; ε — скорость диссипации; — оператор Лапласа (в стандартной форме записи, для решения практических задач, часто используют частные производные только по одному направлению); u — скорость в контрольном объёме (для решения практических задач часто используется логарифмический профиль скорости в пристенной области:

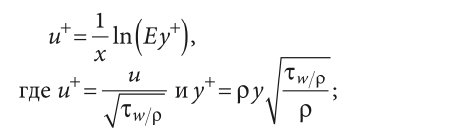
ρ — плотность жидкости (для течений в ограниченных объёмах часто выносится из-под дифференциала);

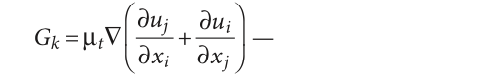
источниковый член, отражающий интенсивность порождения турбулентности в рассматриваемом объёме;

турбулентная вязкость (характеризует интенсивность переноса турбулентных пульсаций); cμ, E, χ и σk — универсальные константы, устанавливаемые экспериментально; τw — касательное напряжение.

Стандартное уравнение k-ε-модели турбулентности для диссипации:

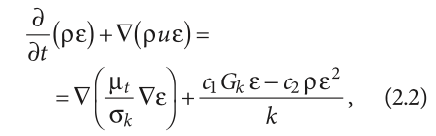
где с1 и с2 — добавочные константы.

Решение уравнений производится через представление о логарифмическом профиле скорости в пристенной области, а также линейности изменения длины пути смешения от расстояния до стенки, что позволяет выразить энергию диссипации следующим образом:

Величина кинетической энергии k рассчитывается из обычного балансового уравнения с учётом отсутствия диффузионного переноса кинетической энергии и включения напряжения трения на стенке.

Из структуры уравнений (2.1) и (2.2) нетрудно заметить, что стандартная k-ε-модель предполагает мгновенную передачу энергии крупных турбулентных вихрей к группам более мелких на всём протяжении потока, что не совсем верно в нашем случае. Такая модель даёт хорошие результаты при условно-равномерном течении, где как образование турбулентных вихрей, так и передача энергии происходят равномерно на всём протяжении течения.

В нашем случае образование основных турбулентных вихрей происходит на входе в канал (в нижней части отопительного прибора) с последующим постепенным распадом на более мелкие по всей длине канала (постепенная стабилизация течения). При этом масштабы зарождающихся вихрей на входе в канал и при движении в канале отличаются на порядок или два порядка (по характерному линейному размеру гидравлических сопротивлений, образующих турбулентность: на входе в канал они определяются всем габаритом отопительного прибора и габаритами конвективной ленты, при движении в канале — только шероховатостью канала, образованного конвективной лентой).

Двухслойная k-ε-модель предполагает деление общей кинетической энергии турбулентных пульсаций k между областью производства и областью передачи турбулентной энергии. В нашем случае это позволяет существенно повысить точность моделирования, так как основные турбулентные пульсации генерируются только на входе в канал и легко учитываются даже при крупной расчётной сетке (в местах генерации турбулентных вихрей сетка намеренно сделана более мелкой, чтобы участок входа потока в отопительный прибор был рассчитан полностью).

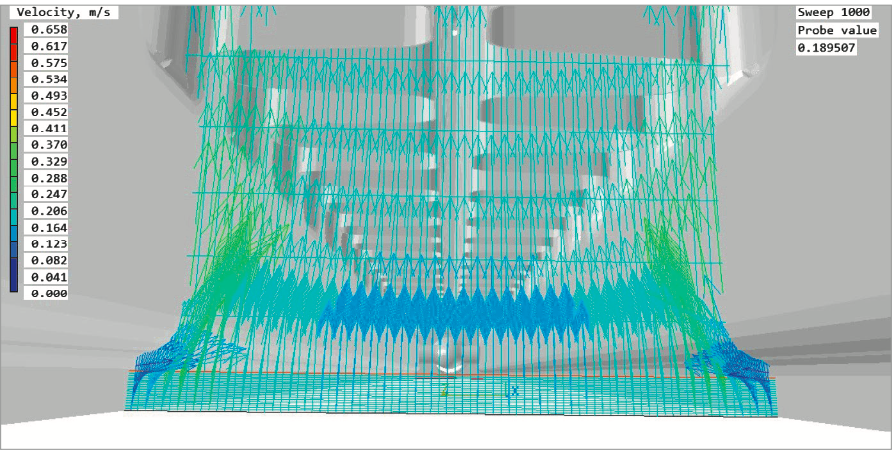
Рис. 3. Схема захода потоков в нижнюю часть радиатора, в конвективную ленту (стрелками показано направление векторов скорости)

На рис. 3 отчётливо видны изменения направления движения потока слева и справа при заходе в отопительный прибор. Заметны существенные увеличения локальных скоростей и изменение их направления. Эти зоны являются основными источниками турбулентных пульсаций, генерации изначальных крупных вихревых образований. Соответственно, их энергия распределяется на поток по всей длине канала и учитывается при формировании поля скоростей в конвективной ленте. А вихри малых размеров, генерируемые шероховатостью канала, фактически не учитываются, как и в стандартной k-ε-модели (что является верным при низких скоростях движения и малых числах Re). В то время как в стандартной k-ε-модели предполагается наличие вихрей одинакового масштаба по всей длине канала, а их масштаб берётся по начальному участку (так как только там можно относительно корректно выделить пристенную область), с учётом крупной сетки расчёта (рис. 4), масштаб которой сопоставим с размером ребра конвективной ленты. Возникает серьёзная погрешность в расчёте поля скоростей из-за невозможности корректной работы с пристенной областью (фактическим её отсутствием в расчётной сетке) по всей длине каналов, что, в свою очередь, ведёт к неточности в определении расхода воздуха, проходящего через отопительный прибор, и остальных ключевых интегральных параметров моделирования.

Рис. 4. Качественное изображение расчёт- ной сетки

Применение мелкой расчётной сетки, которая позволит корректно учитывать пристенные пульсации, существенно увеличивает расчётное время (более чем в 1000 раз) и на такой сложной геометрии приводит к несходимости расчёта для большинства моделей турбулентности. В этом случае необходимо изучать движение в каналах конвективной ленты отдельно, путём последовательного моделирования, что плохо применимо к поставленной задаче и не позволяет выйти на приемлемую точность интегральных характеристик.

Сопоставление расчёта двух моделей турбулентности представлено на рис. 5.

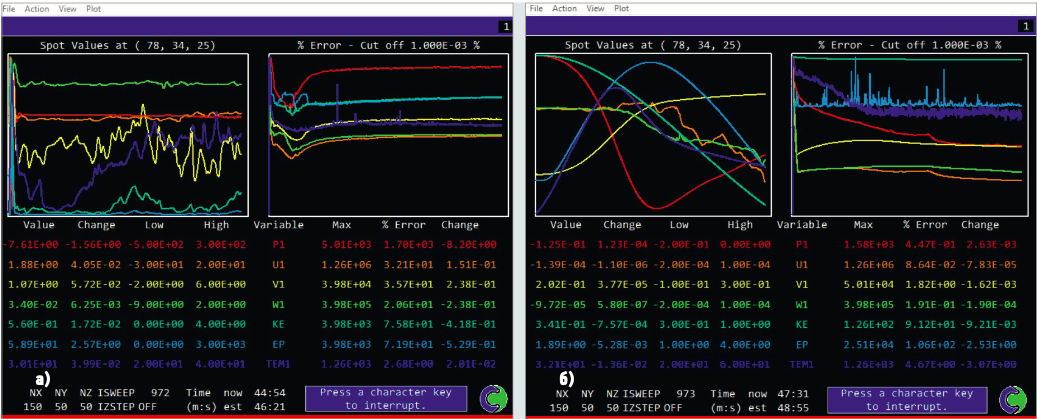
Рис. 5. Завершающий этап расчёта для стандартной (а) и для двухслойной k–ε-модели (б)

Из рис. 5 нетрудно понять, что, несмотря на меньшую итоговую погрешность общего энергетического расчёта (погрешность по температуре составляет 2,68%) для стандартной k-ε-модели (рис. 5а), все остальные величины (скорости по всем направлениям, давление) имеют неприемлемые погрешности (от 20 до 170%). Это как раз связано с некорректным расчётом пристенного поля скоростей на крупной сетке, что вызывает конечную несходимость расчёта. Причём для двухслойной k-ε-модели (рис. 5б) практически все погрешности лежат в пределах 2% (погрешность энергетического расчёта составляет 4,67%, что также приемлемо для подобного моделирования).

Те же выводы можно сделать на основании общего графика изменения расчётных величин (графики слева). На рис. 5а они имеют спонтанный характер без стремления к выравниванию, в то время как на рис. 5б для всех графиков характерен синусоидальный характер, и несмотря на то, что время расчёта не позволило им выйти на «полку», конечная точка находится в середине амплитуды графика.

И для той, и для другой модели характерны высокие погрешности по конечным величинам кинетической энергии турбулентных пульсаций и энергии диссипации, что неудивительно с учётом крупной расчётной сетки и неравномерности потока (радикально разного характера течения на входе и в конвективном канале). Однако ввиду малых абсолютных значений этих величин (условно-ламинарного потока с низкими числами Re), они не вносят сильных погрешностей в расчёт интегральных показателей модели:

Qвн = Gcp(tвых — tвх), (4)

где G — расход воздуха, движущегося за счёт естественной конвекции, кг/с; cp — удельная изобарная теплоёмкость воздуха при средней температуре внутреннего конвективного пространства отопительного прибора, Дж/(кг·К); tвых — средняя температура выходящего воздуха из отопительного прибора, °C; tвх — средняя температура входящего воздуха в отопительный прибор (принимается по температуре окружающей среды tвх = tокр), °C.

Для того чтобы воспользоваться уравнением (4), необходимо произвести моделирование. Общий вид модели представлен на рис. 6. Границы моделируемой области проходят по физическим границам отопительного прибора.

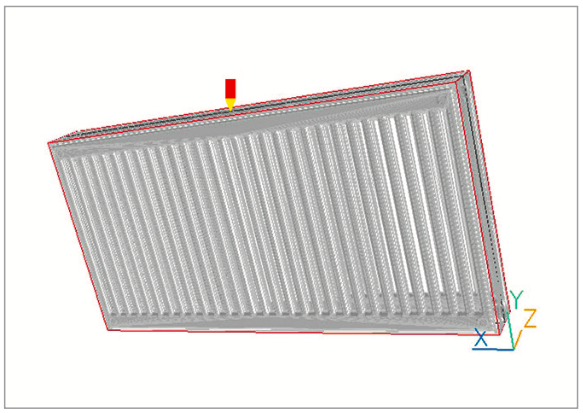
Рис. 6. Общий вид моделируемой области отопительного прибора

Вход воздуха происходит в нижней плоскости xz (y = 0), параметры входа: температура — tвх = tокр = +20°C, давление — атмосферное, размер — по границам отопительного прибора. Фактически это свободный вход в нижнюю плоскость отопительного прибора. Выход воздуха происходит в верхней плоскости xz (y = 500 мм), по выпускной решётке, параметры выхода: температура и давление — по расчёту, размер — по границам отопительного прибора. Фактически это свободный выход в верхнюю плоскость отопительного прибора.

Источник тепла задаётся как постоянная температура (граничные условия первого рода) теплоносителя внутри панелей отопительного прибора, по средней температуре теплоносителя. Направление силы гравитации задаётся противоположным направлению оси Oy.

Результаты моделирования при средней температуре теплоносителя +80°C представлены на рис. 7 и 8.

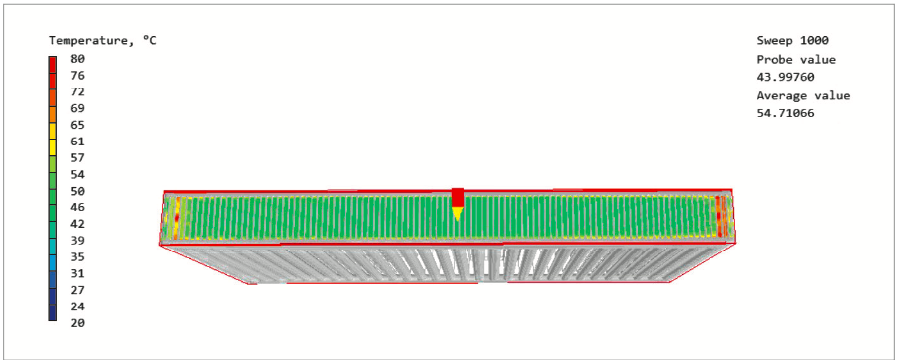
Рис. 7. Распределение температур по плоскости выхода воздуха из отопительного прибора

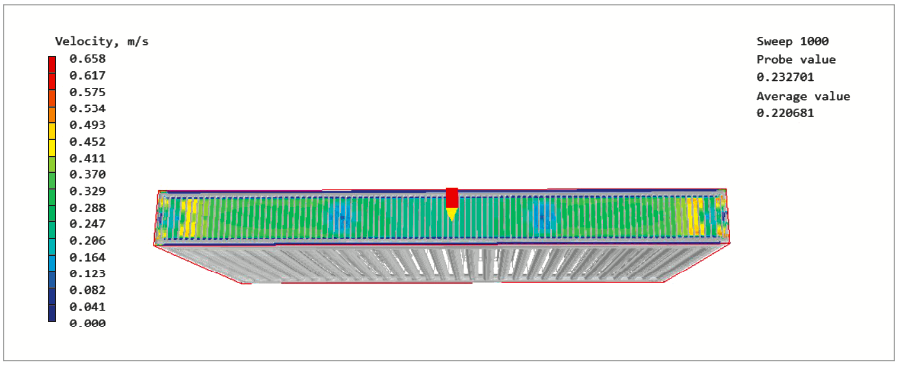
Рис. 8. Распределение скоростей по сечению отопительного прибора

По результатам численного моделирования получаем значения температур и скоростей по верхней и нижней плоскостям отопительного прибора, приведённые в табл. 1.

Внешний конвективный тепловой поток возможно посчитать из стандартных критериальных уравнений естественной конвекции, для движения воздуха вдоль вертикальной поверхности [8]:

Qвнеш = αFконв(tпов — tокр), (5)

здесь F — площадь наружной поверхности отопительного прибора, м²; tпов — температура поверхности отопительного прибора (принимается как средняя температура теплоносителя внутри отопительного прибора, что вполне допустимо, так как коэффициент теплоотдачи со стороны воздуха на два порядка меньше, чем коэффициент теплоотдачи со стороны теплоносителя, причём термическим сопротивлением стенки можно пренебречь — оно составляет менее 1% от общего коэффициента теплопередачи), °C; tокр — температура окружающей среды (учитывая, что отопительный прибор находится в свободном конвективном поле), °C;

α — коэффициент теплоотдачи от наружной поверхности отопительного прибора, Вт/( м²·К):

где d — характерный линейный размер (принимается высота отопительного прибора, как основной определяющий размер в характере формирования течения воздуха вдоль поверхности), м; Nu — критерий Нуссельта для основной теплообменной поверхности; λ — коэффициент теплопроводности воздуха, Вт/(м·К):

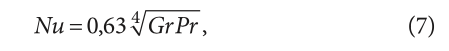
где Pr — критерий Прандтля при средней температуре воздуха; Gr — критерий Грасгофа:

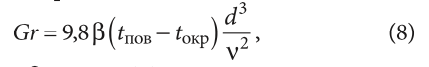
где β — коэффициент температурного расширения воздуха, взятый для средней температуры, между температурой поверхности отопительного прибора и температурой окружающего воздуха; ν — кинематическая вязкость воздуха, м²/c.

Формула (7) применяется для анализа ламинарных течений при естественной конвекции (низких числах Рэлея), что технически правильно для конкретного расчёта, однако это не означает фактическую ламинарность течения.

Турбулентные пульсации возникают в пристенных областях, также не исключены крупные (порядка характерного линейного размера поверхности) вихри при конвективном движении. При этом ламинарность потока при критериальном анализе не нарушается.

Следовательно, нет противоречий в одновременном применении двухслойной k-ε-модели турбулентности и критериального уравнения для ламинарных течений, поскольку применение уравнения для турбулентных течений уместно при очень высокой скорости восхождения потока, порождающей большое количество вихрей среднего размера, то есть бóльших, чем тепловой пограничный слой, но существенно меньших (на порядок), чем характерный линейный размер обтекаемой поверхности.

Фактически мы предполагаем смешанный режим течения, интерпретируемый следующим образом:

• ламинарный на порядках величины теплового пограничного слоя;
• турбулентный в пристенной области (что позволяет предположить наличие большого количества турбулентных пульсаций внутри теплового пограничного слоя);
• турбулентный на удалении порядка размера поверхности, рядом с которой поднимается конвективный поток.

Определённую сложность представляет точное определение всех площадей теплообменной поверхности и правильный их учёт для расчёта тепловых потоков. Основные данные для отопительного прибора «тип 22» размерами 500×1000 мм приведены в табл. 2.

Расчёт количества тепла, передаваемого излучением:

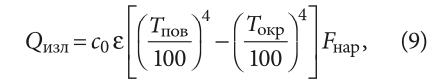
где T — соответствующие температуры в абсолютных значениях, К; c0 — коэффициент излучения абсолютно чёрного тела; ε — степень черноты поверхности отопительного прибора (принимаем ε = 0,9).

Также несложно вычислить средний конвективный коэффициент теплоотдачи при взаимодействии воздуха с конвективной лентой отопительного прибора и с внешними поверхностями отопительного прибора:

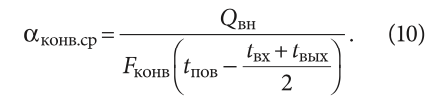
Результаты расчёта сведены в табл. 3.

Таким образом, мы получили расхождение рассчитанного с заявленным и подтверждённым лабораторными испытаниями тепловых потоков менее 9% при попадании в диапазон допустимых тепловых мощностей, то есть аналитическая модель расчёта имеет удовлетворительную точность.

Заключение

Мы рассмотрели базовую численную модель стального панельного радиатора, применённую совместно с аналитическим расчётом. В результате проведённого расчётного исследования можно сделать следующие выводы:

• крайне важна точная оценка площади всех теплопередающих поверхностей отопительного прибора с разделением на конвективные и излучающие;
• применим на практике расчёт совокупной теплоотдачи базовой (без интенсификаторов) модели отопительного прибора путём применения критериальных методов в диапазоне их работы и численного моделирования там, где невозможно применить критериальный метод.
• при численном моделировании рекомендуется применять двухслойную k-ε-модели турбулентности [6, 7].

Полученные результаты применимы для проверки эффективности внедряемых методов увеличения теплоотдачи отопительных приборов.