В настоящее время вопросы энергосбережения и энергоэффективности становятся решающими при выборе и расчёте систем вентиляции и кондиционирования воздуха. Одним из способов снижения энергозатрат в этих системах является использование теплоутилизационного оборудования, в том числе в комбинации с испарительным охлаждением и некоторыми другими техническими решениями [1–7]. Однако, помимо расчётных теплофизических параметров, таких как температура и влажность приточного и удаляемого воздуха, оказывающих существенное влияние на интенсивность теплообмена между встречными потоками в подобных аппаратах, в значительной степени на эффективность теплообменных процессов влияет и конструктивное исполнение самой теплоутилизирующей установки.
Задача расчёта температурной эффективности пластинчатого рекуператора является важным звеном в улучшении конструктивных свойств оборудования, что должно привести к максимальному снижению потребления теплоты в приточно-вытяжной установке (ПВУ). В процессе данного исследования и в результате расчёта будет показано, насколько способна измениться картина, отражающая зависимость коэффициента температурной эффективности kэф, в рассматриваемом варианте пластинчатого перекрёстно-точного рекуператора, от изменения расстояния между пластинами в аппарате, а также от размеров самих пластин.
Изначально можно предположить, что величина kэф должна определённым образом изменяться в соответствии с изменением типоразмера установки. Однако необходимо выяснить, как при прочих равных условиях, в первую очередь при совпадении расходов приточного и удаляемого воздуха, обеспечивающего наибольшую эффективность рекуператора, будет выглядеть функция, описывающая данную зависимость.
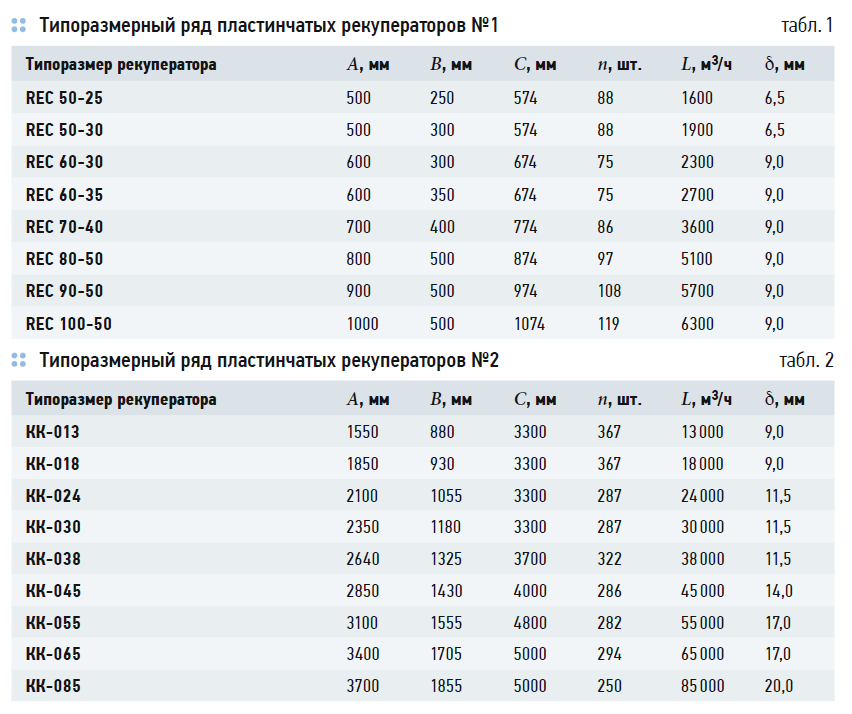
Таким образом, целью расчёта в данном случае является выявление вида функциональной взаимосвязи значения kэф и типоразмера приточно-вытяжного агрегата, определяемого его номинальной воздухопроизводительностью. В качестве основной задачи работы можно рассматривать расчёт величины kэф для различных вариантов аппаратов и оценку влияния на неё изменения их габаритов. Для возможности сравнения получаемых результатов выполним вычисления для двух модельных рядов*, имеющих характеристики, представленные в табл. 1 и 2. Конструкция исследуемых теплообменников изображена на рис. 1.
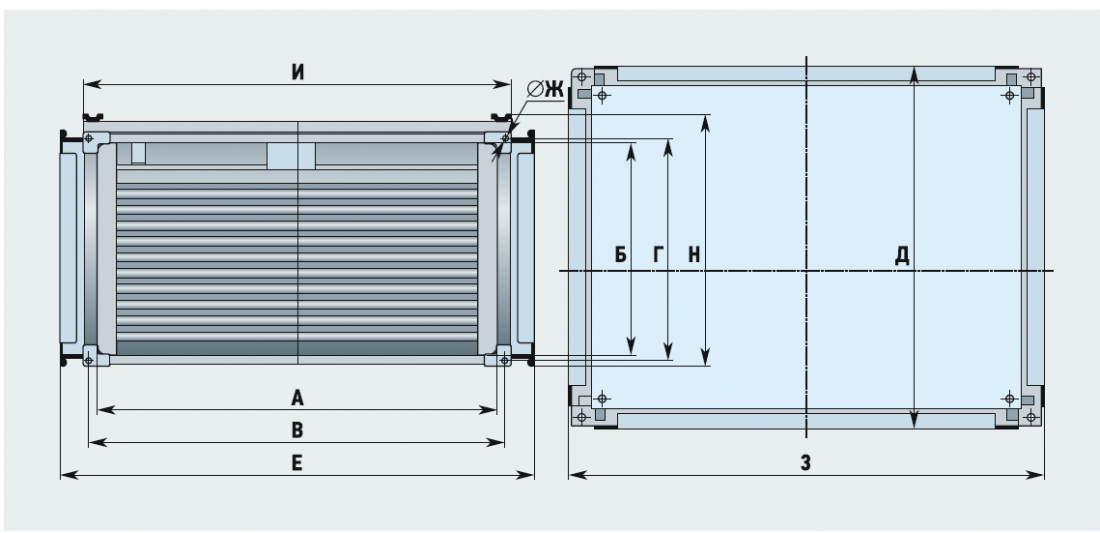
Рис. 1. Схема пластинчатого рекуператора
Для начала расчёта зададимся следующими исходными данными: tн — температура наружного воздуха в холодный период, принимаемая равной средней температуре наиболее холодной пятидневки обеспеченностью 0,92 в Москве по СП 131.13330.2012 «Строительная климатология» tн = −25°C; tу — температура удаляемого воздуха, принимаем tу = +22°C.
Последовательность расчёта
Общепринятое определение kэф пластинчатого рекуператора может быть записано в виде формулы (1) [7–10]:

где tут — температура наружного воздуха, подогретого в аппарате. Однако данная формула непосредственно не учитывает конструктивного исполнения теплообменника, а отражает только физический смысл величины kэф. Для её расчёта воспользуемся методикой [7–10], использующей безразмерные параметры, включающие конструктивные характеристики рекуператора и параметры потоков воздуха в нём. Тогда основное выражение для перекрёстной схемы движения теплоносителей будет выглядеть так:
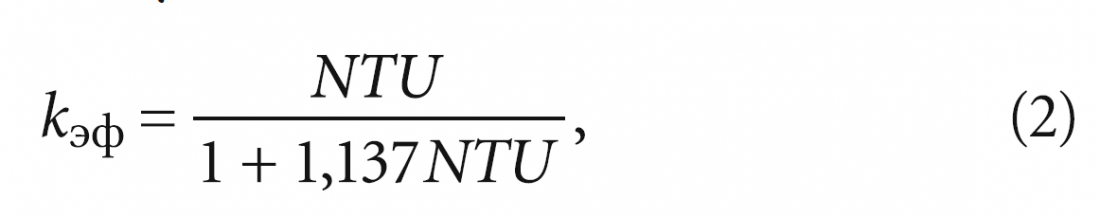
где NTU — безразмерное число единиц переноса теплоты для теплоутилизационного оборудования рассматриваемой системы приточной вентиляции или кондиционирования и вентиляции:

где L — объёмный расход воздуха в установке, м³/ч; с — удельная теплоёмкость воздуха, принимаемая равной 1,005 кДж/(кг∙К); K — коэффициент теплопередачи соответствующего теплообменника, Вт/( м²∙К); F — поверхность теплообмена, м²; ρ — плотность воздуха, кг/м³.
Далее вычислим среднюю плотность воздуха в рекуператоре:
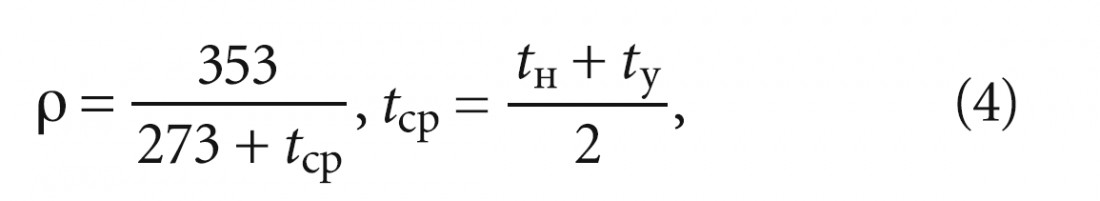
где tср — средняя температура воздуха в аппарате, °C. Отсюда получим:
tср = 0,5×(-25 + 22) = −1,5°C;
ρ = 353/(273–1,5) = 1,3 кг/м³.
Тогда, если пренебречь термическим сопротивлением пластины как незначительным и считать коэффициенты конвективного теплообмена α [Вт/( м²∙К)] с обеих её сторон одинаковыми, что вполне можно допустить при равенстве расходов притока и вытяжки и одинаковой ширине каналов в аппарате, можно считать, что K = α/2. Для определения α лучше всего воспользоваться критериальными уравнениями для безразмерного числа Нуссельта Nu = αl/λ, где l — характерный размер, м; λ — теплопроводность воздуха, равная примерно 0,024 Вт/(м∙К), откуда α = Nu(λ/l).
Рассмотрим два варианта расчёта конвективного теплообмена в теплоутилизирующей установке. По их результатам можно выявить наиболее достоверный способ определения α и в целом kэф.
Вариант 1. Обтекание пластины. Здесь за определяющий размер принимается длина пластины по направлению движения воздуха, в табл. 1 и 2 указанная как сторона A, м. В этом случае можно записать следующее соотношение [7, 8]:
Nu = 0,037Re0,8Pr0,43. (5)
Вариант 2. Расчёт по толщине канала δ. Здесь определяющий размер принимается толщина канала рекуператора. Принимаем за характерный размер δ, м.
Nu = 0,021Re0,8Pr0,43, (5a)
где Re — число Рейнольдса для воздуха — Re = υl/v, где v — скорость воздушного потока, м/с; υ = 1,32×10–6 м²/с — кинематическая вязкость воздуха; Pr = vcρ/λ — число Прандтля, которое для воздуха можно считать равным 0,7. При этом v:
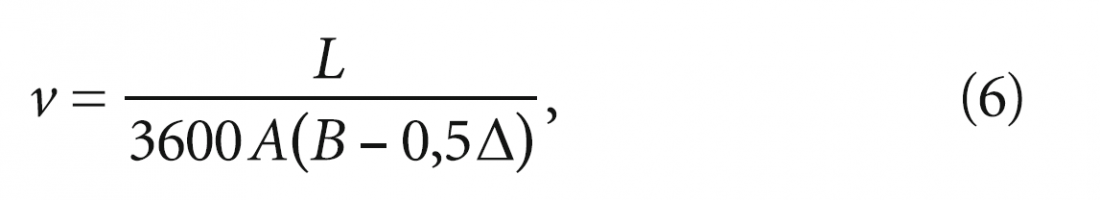
где A и B — длина и ширина пластины, м; n — число пластин в пакете, шт. (табл. 1 и 2), а определение основных конструктивных параметров рассматриваемых модельных рядов пластинчатых рекуператоров было выполнено на основе методики, описанной в [10]. В частности, n = C/d, где C — длина пакета, мм; d — расстояние между пластинами, мм (табл. 1 и 2); ∆ — толщина пластины, мм. Принимаем ∆ = 0,00025 м = 0,25 мм.
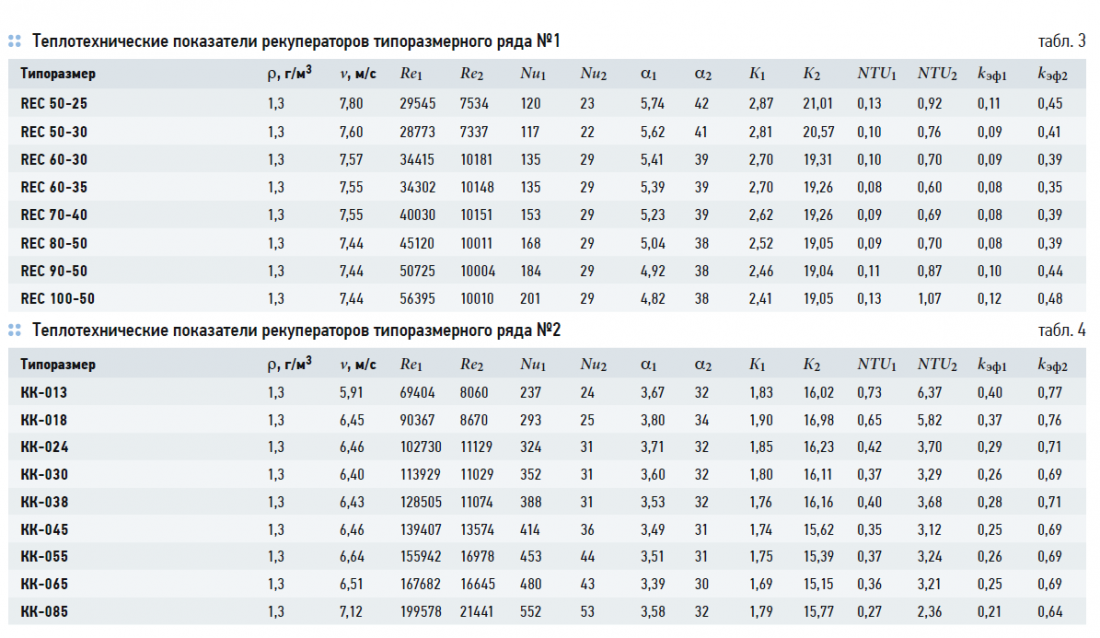
Полученные результаты расчётов по обоим вариантам сведены в табл. 3 и 4. Соответствующие зависимости для коэффициента температурной эффективности kэф и их графические аппроксимации приведены на рис. 2.
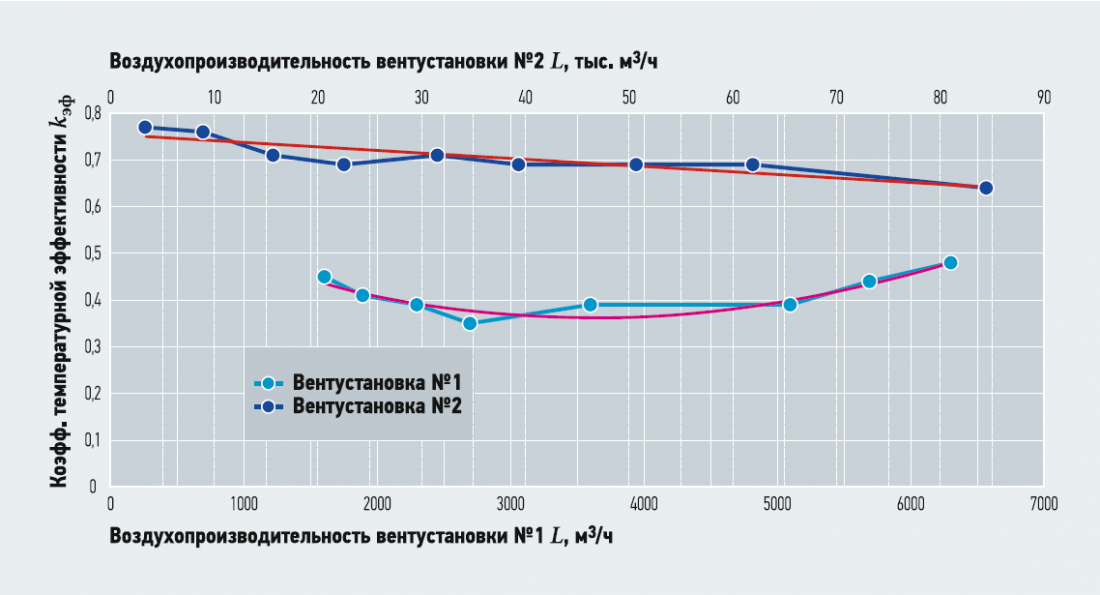
Рис. 2. Зависимости эффективности рекуператоров от воздухопроизводительности установки С. 236–243.
для типоразмерных рядов №№ 1 и 2
На основании полученных данных можно заметить, что вычисление α по второму варианту даёт значительно более достоверные значения, сопоставимые с величинами, измеренными в режиме реальной работы перекрёстно-точного пластинчатого рекуператора [10], поэтому именно их и следует использовать для окончательного определения kэф.
Заключение
По результатам расчёта можно сделать следующие выводы:
1. Из двух методов определения коэффициента конвективного теплообмена на поверхностях пластин наиболее достоверным является расчёт с использованием ширины каналов в качестве характерного размера.
2. Установки ряда №1 работают в зоне наименьшего уровня kэф, что подтверждает предположение о влиянии типоразмера установки, а значит, и пропускаемого расхода воздуха на тепловую эффективность пластинчатого рекуператора.
3. Из-за варьирования ширины каналов между пластинами непропорционально изменению их размера, с увеличением значений расхода kэф начинает падать.
4. Наибольшую величину kэф пластинчатый рекуператор обеспечивает при увеличении числа пластин и пропорциональном изменении ширины канала без снижения скорости перемещения воздуха, что приводит к сохранению геометрического подобия аппаратов в пределах рассматриваемой серии. Оптимальное значение этой скорости лежит в диапазоне 6–7 м/с.

























