Статья ВАК: CFD-моделирование гидравлических режимов тепловых сетей

Введение

Вычислительная гидродинамика (Computational Fluid Dynamics Modeling, CFD), известная как «трёхмерное гидравлическое моделирование», представляет собой практический способ прогнозирования и визуализации потоков жидкости в реальных условиях. С её помощью мы можем понять, как поведёт себя теплоноситель в системе теплоснабжения.

Основное преимущество использования данного метода CFD-исследования заключается в точности результатов. Мы опишем возможность регулирования пьезометрического графика тепловой сети в программах CFD, а именно регулирование гидростатического давления на байпасе, и на основе полученных данных решим вопрос о разработке нового расчётного метода проектирования тепловых сетей, а также рассмотрим технические недостатки, которые могут встретиться на практике. Цифровые данные, конечно, дают ответы на поставленные вопросы, но для принятия оперативных решений целесообразно воспользоваться преимуществами визуализации расчётов, в частности, CFD-моделированием [1].

Основной раздел

Энергосбережение в теплоснабжении является одним из наиболее актуальных вопросов [2]. Эффективное функционирование систем теплоснабжения во многом зависит от режимов работы тепловой сети [3, 4]. Именно поэтому важно оптимизировать гидравлические режимы в сложных системах. Математическому моделированию перемещения тепловых потоков в трубопроводных системах посвящены работы [5, 6], экспериментальному исследованию — работы [7–9].

Абстрактный пример экспериментальной модели и её симулирования методами CFD-моделирования в гидравлике. Представлена модель «гидравлического прыжка» (по Валеро и др.), с входным числом Фруда около 6,0, и её симуляция численными методами (по Байону и др.)

Изучение гидравлических режимов работы системы в реальном времени, их влияние на гидравлическую устойчивость тепловой сети наиболее наглядно показано в CFD-моделировании. CFD позволяет смоделировать тепловую сеть для визуализации технических решений, и его главным преимуществом является получение результатов высокой точности, а недостатком — сильная зависимость результатов от качества смоделированной расчётной сетки модели, ведь чем сложнее структура модели, тем больше ресурсов необходимо для расчёта.

В качестве одного из примеров рассмотрим узел подпитки тепловой сети, представленный на рис. 1.

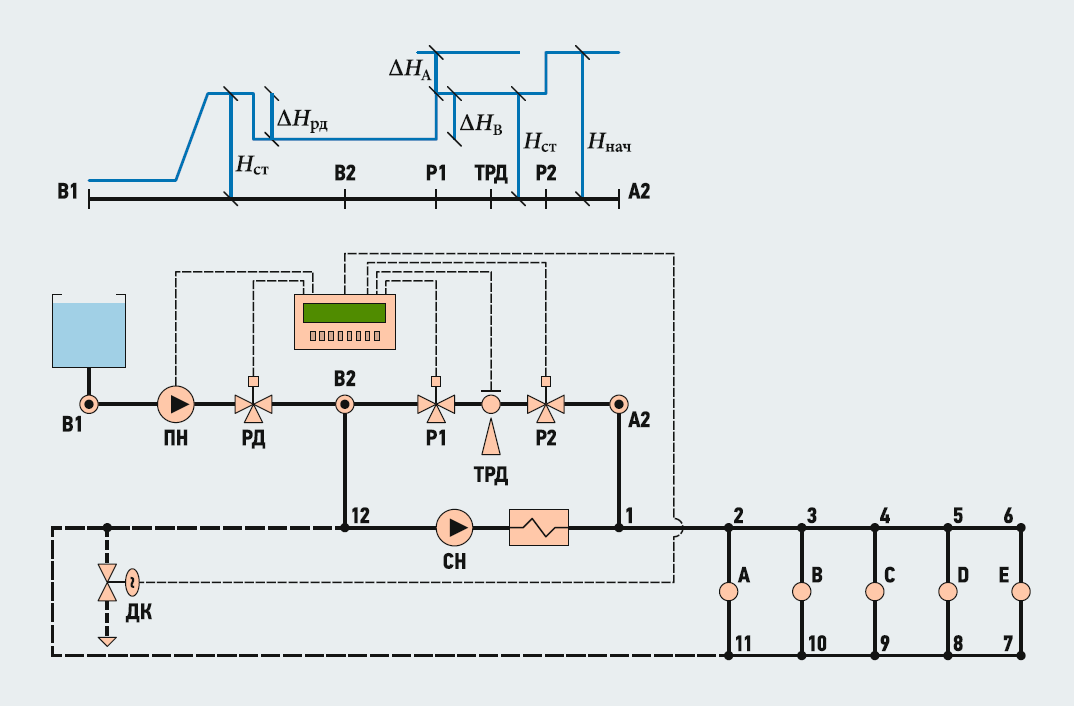
Рис. 1. Принципиальная схема тепловой сети (ПН — подпиточный насос; РД — регулятор давления; ДК — дросселирующий клапан; P2 — регулирующий вентиль № 2; P1 — регулирующий вентиль № 1; ТРД — нейтральная точка или точка регулируемого давления; Hсн — напор сетевого насоса; СН — сетевой насос; П1 — подающий трубопровод; 7–11 — обратный трубопровод; 1–6 —подающий трубопровод; Hст — статическое давление в сети; ΔHрд — потери давления на регуляторе давления; ΔHA — потери давления на регулирующем вентиле р1; ΔHВ — потери давления на регулирующем вентиле № 2; Hнач — начальное давление, равное ΔHст + Hсн)

После выполнения гидравлических расчётов, с учётом особенностей поведения коэффициента гидравлического трения [4] и построения пьезометрического графика, переводим объект исследования в математический вид для расчёта с помощью программы математического моделирования. Для расчёта отключения потребителя смоделируем замкнутую цепь с пятью контурами теплопотребления А, В, С, D и E.

Производим расчёт в программном комплексе SolidWorks. Полученные результаты приведены на рис. 2.

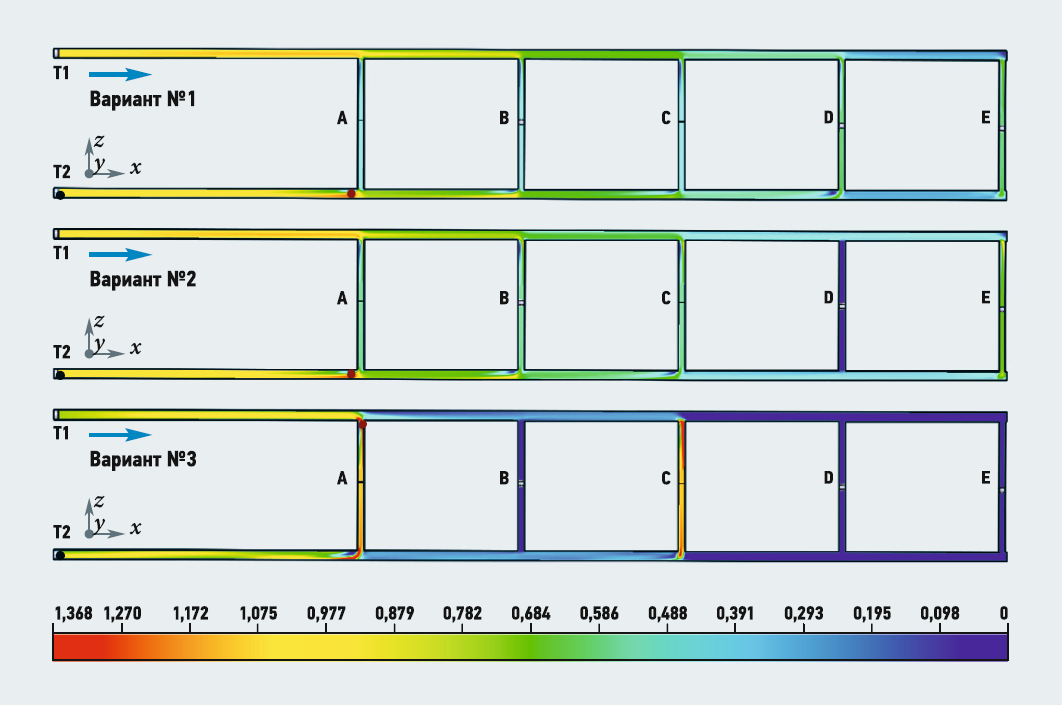
Рис. 2. График скорости теплоносителя в трубопроводе

На нём отображены точечные параметры по длине трубопровода циркуляционных колец, представленных на рис. 1.

Смоделируем отключение одного потребителя (вариант 2) и отключение трёх потребителей (вариант 3). Для варианта 2: в результате расчёта наблюдается отклонение фактического расхода Gф от расчётной величины Gp, что вызывает гидравлическую разрегулировку абонентских систем. Отключение части нагрузки приводит к снижению потерь давления в сети и к росту располагаемых давлений и расхода воды у оставшихся абонентов.

Вариант 2 указывает на небольшое увеличение скорости на потребителях, а вариант 3 с отключением двух и более потребителей показывает избыток скорости на потребителях А и С. Вместе с ростом скорости растут потери давления.

Изменение скорости теплоносителя при отключении потребителей (варианты 2 и 3) показано на рис. 2.

Поскольку с ростом скорости на потребителях возрастают и потери давления, это сказывается на работе сетевого насоса, поэтому возникает риск избытка давления на конечном потребителе.

Рассмотрим пьезометрический график узла подпитки, пьезометрический график и принципиальную схему байпаса, представленную на рис. 1. Параметры: ∆HA = 3 м вод. ст., ∆HB = 21 м, Hст = 57 м, ∆Hрд = 21 м и Hнач = 76 м вод. ст. Принцип действия регулирования описан далее.

Давление в нейтральной точке регулируется регулирующими вентилями P1 и P2 (рис. 1). То есть, если начать прикрывать или полностью закрыть регулирующий вентиль P1, то давление в нейтральной точке будет стремиться к давлению, равному нагнетанию на сетевом насосе, и пьезометрический график начнёт опускаться параллельно оси Oy до минимального упора, и в системе будет наблюдаться аварийный режим. Если прикрывать регулирующий вентиль P2, то давление в нейтральной точке будет стремиться к давлению на входе сетевого насоса, и пьезометрический график начнёт подниматься вверх параллельно оси Oy.

Далее рассмотрим регулирование гидростатического давления в узле подпитки тепловой сети. Подпиточный насос развивает напор Hст. Напор на байпасной линии в точке регулируемого давления (ТРД) равен Hст. В регулирующем вентиле P1 есть напор ∆HA, и полный напор после него рассчитывается как H01 = Hнач — ∆HP2. В задвижке P2 напор H02 = Hст — ∆HP1. Регулятор давления поддерживает постоянное давление в точке ТРД между регулирующими вентилями P1 и P2, при этом в точке после P1 будет поддерживаться напор H01.

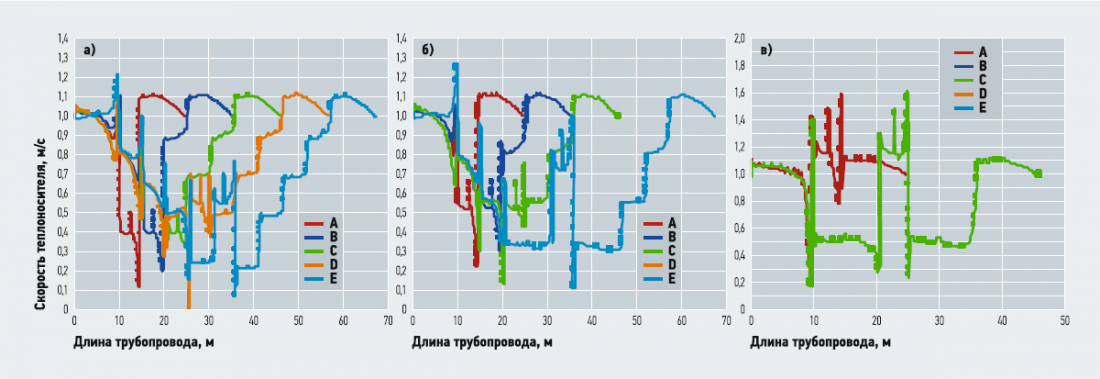
Рис. 3. График скоростей тепловой сети на каждом циркуляционном кольце (а — вариант №1, б — вариант №2, в — вариант №3)

Для определения необходимого прикрытия клапана и получения требуемых значений воспользуемся авторской расчётной методикой, реализованной в Excel. Согласно разработанной методике, степень прикрытия составляет 40%. Малый пьезометр после прикрытия клапана с параметрами ∆HA = 19 м вод. ст., ∆HB = 21 м, Hст = 57 м, ∆Hрд = 21 м и Hнач = 76 м вод. ст. представлен на рис. 3.

Заключение

Показана целесообразность использования CFD-моделирования для практических инженерных расчётов. Подобные численные эксперименты по визуализации гидравлических режимов работы, как отдельных элементов, так и всей системы теплоснабжения в целом, позволяют принимать обоснованные технические решения, а полученные результаты дают возможность проанализировать последствия принимаемых управленческих решений на гидравлическую устойчивость. Появляется возможность оперативного внесения надлежащих корректив в данные технические решения для повышения надёжности и живучести инженерных систем зданий и тепловых сетей.